【図解】グラフの平行移動の意味、イメージ、証明と例題について

1. 平行移動とは?
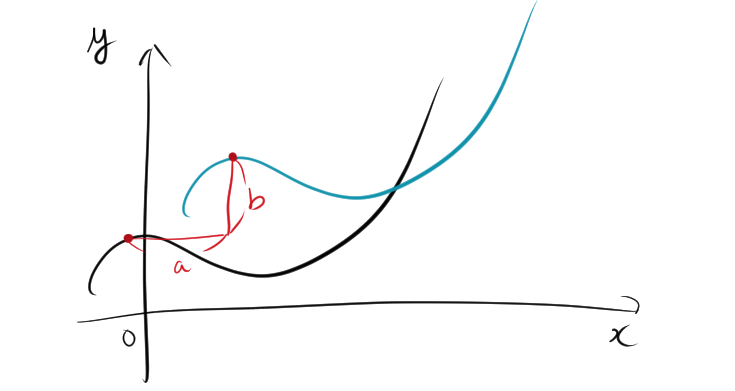
平行移動とは、グラフ全体を上下または左右に一定の距離だけずらす操作のことです。この操作により、グラフの形状は変わらず、位置だけが変化します。
$$y-b = f(x-a)$$
となる。
平行移動の直感的な意味を考えると、グラフ全体が特定の方向にスライドするようなイメージです。具体的には、次のように理解できます。
1.1. x軸方向の平行移動の直感的な意味
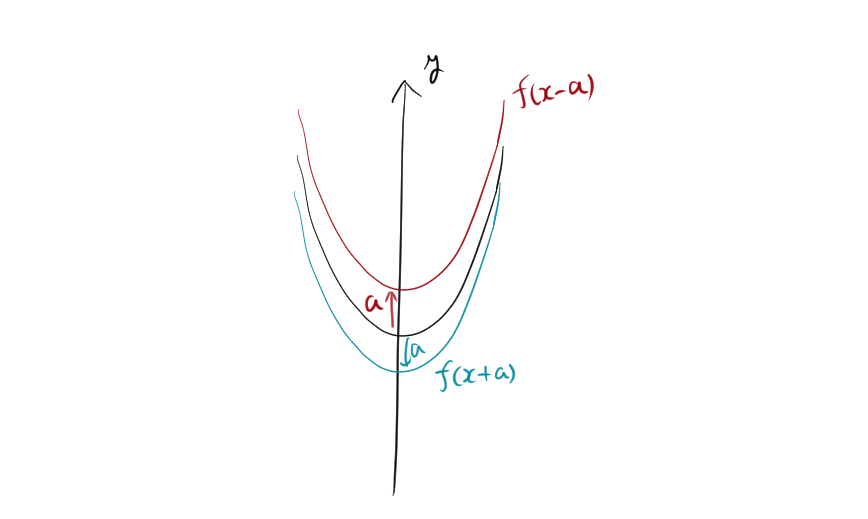
- 右方向(正のx方向)に平行移動すると、グラフは右にスライドします。例えば、関数 \( f(x) \) を右に \( a \) だけ平行移動する場合、関数は \( f(x – a) \) に変わります。グラフ全体が \( a \) だけ右にずれるイメージです。
- 左方向(負のx方向)に平行移動すると、グラフは左にスライドします。このとき、関数は \( f(x + a) \) の形になります。
1.2. y軸方向の平行移動の直感的な意味
- 上方向(正のy方向)に平行移動すると、グラフ全体が上に持ち上がるイメージです。関数 \( f(x) \) を上に \( b \) だけ平行移動する場合、関数は \( f(x) + b \) になります。
- 下方向(負のy方向)に平行移動すると、グラフ全体が下にスライドします。この場合、関数は \( f(x) – b \) になります。
2. 平行移動の証明
2.1. 証明の方針
座標 \((x_0, y_0)\) が \(x\) 軸方向に \(a\)、\(y\) 軸方向に \(b\) だけ移動したとしてその座標を(X,Y)とする。
2.2. 証明
座標 \((x_0, y_0)\) が \(x\) 軸方向に \(a\)、\(y\) 軸方向に \(b\) だけ移動したと考えると、新しい座標を \((X, Y)\) と表すことができます。この場合、\((X, Y)\) と \((x_0, y_0)\) の関係は以下のようになります。
\[ X = x_0 + a, \quad Y = y_0 + b \]
これを元に、逆に \((x_0, y_0)\) を求めると、
\[ x_0 = X – a, \quad y_0 = Y – b \]
\(y_0 = f(x_0)\)より、
\[ Y – b = f(X – a) \]
となります。
3. グラフの移動の例題
3.1. 例題1:2次関数
- \( x \) 軸方向に 3だけ移動
- \( y \) 軸方向に 2だけ移動
\( x \) 軸方向の平行移動\( x \) 軸方向に 3 単位右に移動する場合、元の関数 \( y = x^2 \) の \( x \) の部分を \( (x – 3) \) に置き換えます。これにより、式は次のように変わります。
\[ y = (x – 3)^2 \]
\( y \) 軸方向の平行移動\( y \) 軸方向に 2 単位上に移動する場合、関数全体に 2 を足します。したがって、式は次のように変わります。
\[ y = (x – 3)^2 + 2 \]
求める平行移動後のグラフの式は次の通りです。
\[ y = (x – 3)^2 + 2 \]
展開すると
\[ y =x^2-6x + 11 \]
3.2. 例題2:3次関数
- \( x \) 軸方向に -4だけ移動
- \( y \) 軸方向に -1だけ移動
\( x \) 軸方向に -4だけ移動するために、 \( x \) の部分を \( x + 4 \) にすると
\[ y = (x + 4)^3 + (x + 4) \]
\( y \) 軸方向に -1だけ移動するには、 \( y \) の部分を$y+1$にすると、
\[ y = (x + 4)^3 + (x + 4) – 1 \]
展開すると、
\[ \begin{align*} (x + 4)^3 + (x + 4) – 1 &= (x^3 + 12x^2 + 48x + 64) + (x + 4) – 1 \\ &= x^3 + 12x^2 + 48x + x + 64 + 4 – 1 \\ &= x^3 + 12x^2 + 49x + 67 \end{align*} \]
したがって、展開後の関数は
\[ y = x^3 + 12x^2 + 49x + 67 \]