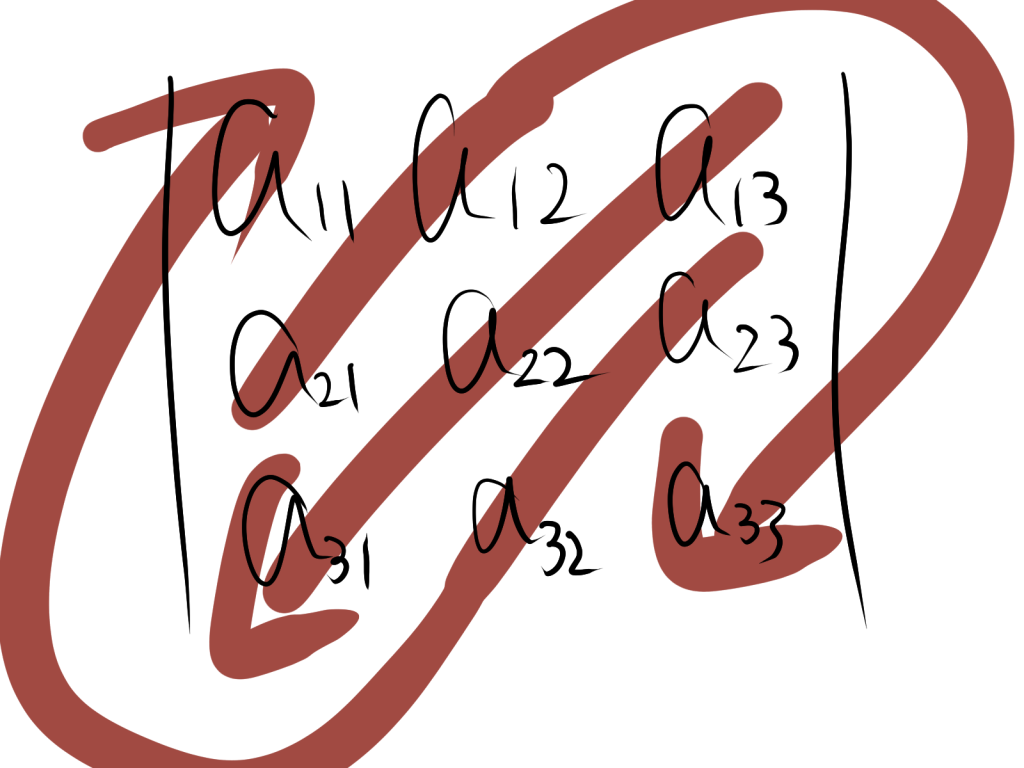2次・3次の行列式の計算方法・具体例・例題について
1. 行列式とは
行列式とは、正方行列に対して定義される特別な計算方法です。行列式は通常、行列を縦棒 \( | \) で囲むか、`det`という記号を使って表現されます。2次行列や3次行列の行列式は、計算が比較的簡単であり、特に2次の場合には「サラスの公式」として知られています。
1.1. 具体例
2次の行列式は次のようになります。
\[ \begin{vmatrix} 1 & 4 \\ 99 & 2 \\ \end{vmatrix} \]
2. 2次行列の場合の行列式
2次の正方行列（2×2行列）の行列式は、次のように計算されます。
\[ \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{vmatrix} = a_{11} \cdot a_{22} – a_{12} \cdot a_{21} \]
これは、行列の対角要素 \( a_{11} \) と \( a_{22} \) を掛けた値から、その他の対角線の要素 \( a_{12} \) と \( a_{21} \) を掛けた値を引くことで求められます。
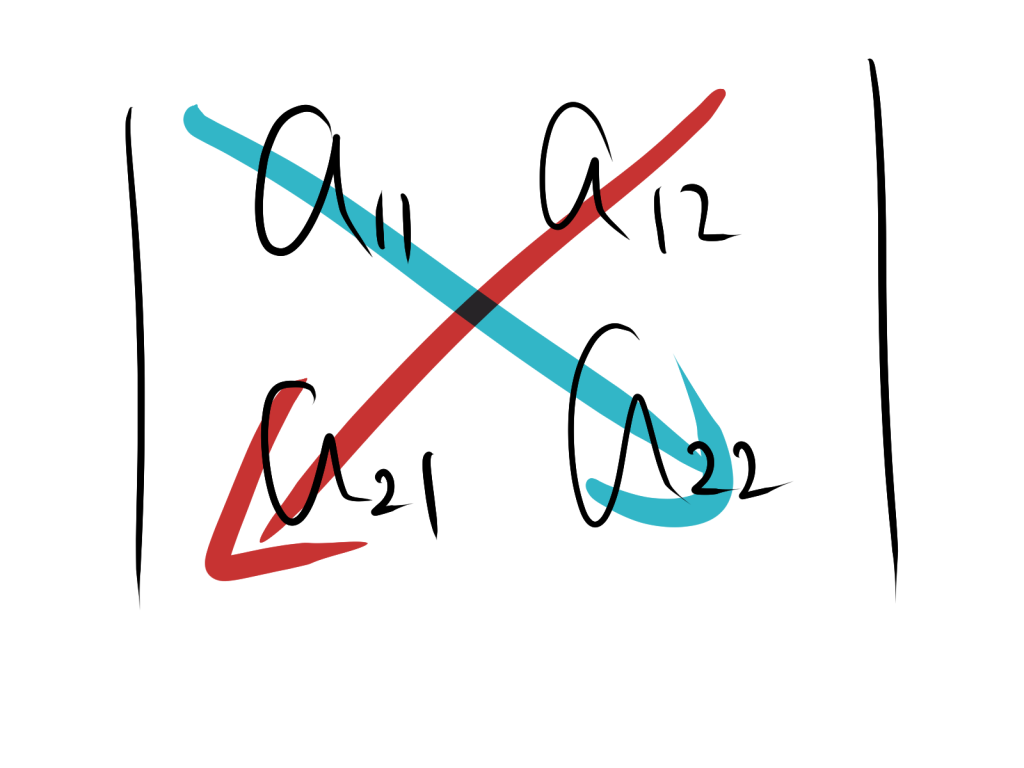
2.1. 2次の行列式の視覚的理解
下図を見てみましょう。青い矢印で示された部分が正の符号を持つ項、赤い矢印で示された部分が負の符号を持つ項を表しています。
3. 3次行列の場合の行列式
3次の正方行列（3×3行列）の行列式は、より複雑ですが、以下のように計算されます。
\[ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} – a_{11}a_{23}a_{32} – a_{12}a_{21}a_{33} – a_{13}a_{22}a_{31} \]
ここでは、6つの項を足し合わせています。
3.1. 3次の行列式の視覚的理解
3次行列の行列式は、項が6つ存在するため、それらを2つの図に分けて視覚的に確認しましょう。以下の図で、青い矢印が正の符号を持つ項、赤い矢印が負の符号を持つ項を表しています。
まず、正の符号を持つ部分です。
次に、負の符号を持つ部分です。
4. 行列式の計算問題
4.1. 2次の行列式の例題
$A=\begin{bmatrix}
1 & 2 \\
3 & 4 \\
\end{bmatrix}$、$B=\begin{bmatrix}
-2 & 5 \\
1 & -3 \\
\end{bmatrix}$、$C=\begin{bmatrix}
0 & -1 \\
2 & 3 \\
\end{bmatrix}$
それぞれの行列式を計算せよ。
計算は以下のようになる。
$\mathrm{det}A$
$=\begin{vmatrix} 1 & 2 \\ 3 & 4 \\ \end{vmatrix}$
$=1\times4-2\times3$
$=-2$
$\mathrm{det}B$
$=\begin{vmatrix} -2 & 5 \\ 1 & -3 \\ \end{vmatrix}$
$=-2\times(-3)-1\times5$
$=1$
$\mathrm{det}C$
$=\begin{vmatrix} 0 & -1 \\ 2 & 3 \\ \end{vmatrix}$
$=0\times3-(-1)\times2$
$=2$
4.2. 3次の行列式の例題
正方行列A,B,Cを以下のようにする。
$A=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{bmatrix}$、$B=\begin{bmatrix} 2 & 0 & -1 \\ 1 & 3 & 2 \\ -3 & 4 & 1 \\ \end{bmatrix}$
それぞれの行列式を計算せよ。
計算は以下のようになる。
$\mathrm{det}A=\begin{vmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{vmatrix}$
$=45+84+96-72-105-48$
$=0$
$\mathrm{det}B=\begin{vmatrix} -1 & 0 & 1 \\ 0 & -2 & 1 \\ -2 & 1 & 0 \\ \end{vmatrix}$
$=0-(4-1)$
$=-3$
