【三角形の面積を求める】ヘロンの公式の例題と証明について

はるか

ヘロンの公式、覚えた？

ふゅか

もちろん！三角形の3辺がわかれば面積が求められるんだよね。便利だよね～！

はるか

うん。公式自体もシンプルだし、条件がそろっていれば実用的。

1. ヘロンの公式

ここで、$S$は三角形の面積、$a$,$b$,$c$はそれぞれ三角形の3辺の長さを表し、$s = \dfrac{a+b+c}{2}$として定義されます。

2. 例題

2.1. ヘロンの公式の例題1

$a = 5$、$b = 6$、$c = 7$からsを求めると、

$$s = \dfrac{5+6+7}{2} = 9$$

となります。三角形の面積 $S$ は、ヘロンの公式を用いると、

$$S = \sqrt{9(9-5)(9-6)(9-7)} = \sqrt{9\times 4\times 3\times 2} = 6\sqrt{6}$$

2.2. ヘロンの公式の例題2

$a = 5$、$b = 6$、$c = 8$を代入すると、

$$s = \dfrac{5+6+8}{2} = \dfrac{19}{2}$$

となります。三角形の面積 $S$ は、ヘロンの公式を用いると、

$$\begin{align*} S &= \sqrt{\dfrac{19}{2}\left(\dfrac{19}{2}-5\right)\left(\dfrac{19}{2}-6\right)\left(\dfrac{19}{2}-8\right)} \notag \\ &= \sqrt{\dfrac{19}{2} \times \dfrac{9}{2} \times \dfrac{7}{2} \times \dfrac{3}{2}} \notag \\ &= \dfrac{3}{4}\sqrt{19 \times 7 \times 3} \notag \\ &= \dfrac{3}{4}\sqrt{399} \end{align*}$$

3. ヘロンの公式の証明

ヘロンの公式は、三角形の三辺の長さからその面積を求める公式です。以下にその証明を示します。

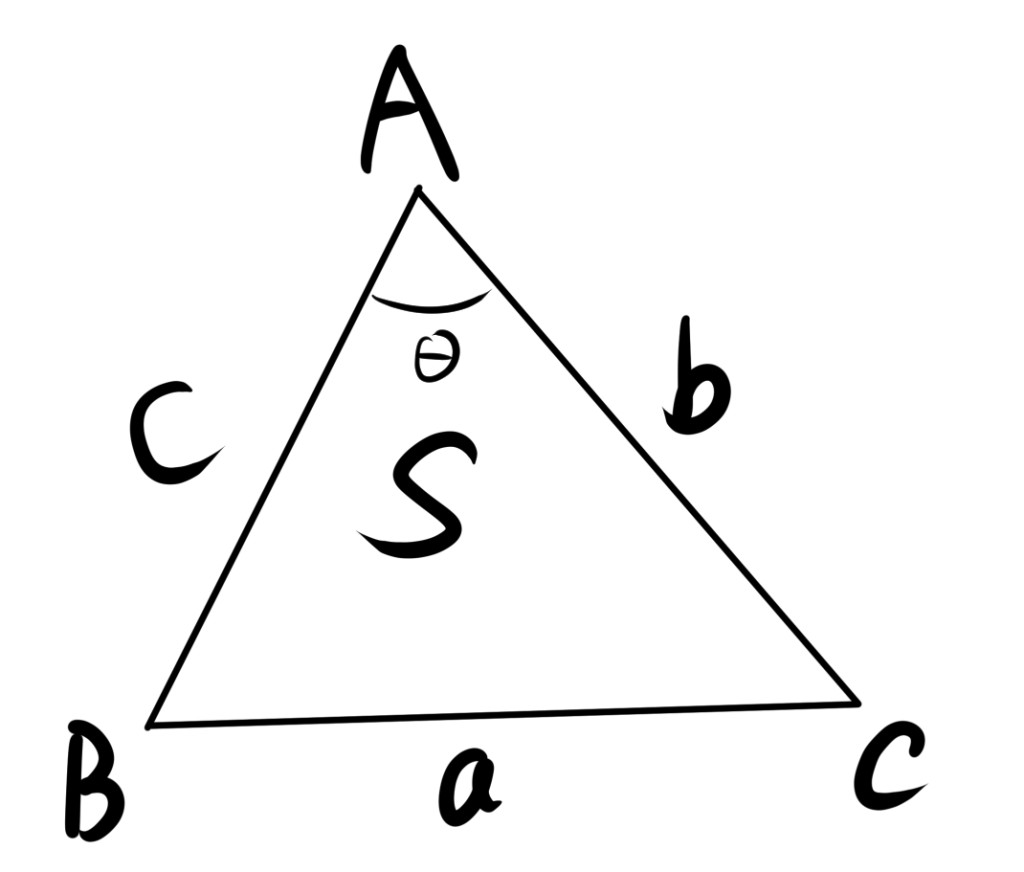
まず、三角形の三辺の長さをそれぞれ $a,b,c$ とします。

三角形の面積 $S$ は、sinを用いた三角形の面積の求め方より、

$$S =\dfrac{1}{2}bc\sin\theta$$

と表せます。$\sin\theta=\sqrt{1-\cos^2\theta}$を用いると、三角形の面積は

$$\begin{align*} S &= \dfrac{1}{2}bc\sin\theta \notag \\ &= \dfrac{1}{4}\sqrt{4b^2c^2(1-\cos^2\theta)} \end{align*}$$

とも表せます。また、余弦定理を用いると、$\cos\theta=\dfrac{b^2+c^2-a^2}{2bc}$ が成り立つため、式変形を行うと、

$$\begin{align*} &= \dfrac{1}{4}\sqrt{4b^2c^2(1-\cos^2\theta)} \notag \\ &= \dfrac{1}{4}\sqrt{4b^2c^2 – (b^2+c^2-a^2)^2} \notag \\ &= \dfrac{1}{4}\sqrt{\lbrace 2bc – (b^2+c^2-a^2) \rbrace \lbrace 2bc + (b^2+c^2-a^2) \rbrace} \notag \\ &= \dfrac{1}{4}\sqrt{\lbrace a^2 – (b-c)^2 \rbrace \lbrace (b+c)^2 – a^2 \rbrace} \notag \\ &= \dfrac{1}{4}\sqrt{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)} \end{align*}$$

となります。$a+b+c=2s$　$\left(s=\dfrac{a+b+c}{2}\right)$と置くと、

$$\begin{align*} &= \dfrac{1}{4}\sqrt{2s(2s-2a)(2s-2b)(2s-2c)} \notag \\ &= \sqrt{s(s-a)(s-b)(s-c)} \end{align*}$$

このように、三角形の辺の長さだけで面積を求める方法があることがわかりました。

はるか

$\cos\theta$と余弦定理を使って面積を変形するところ、ポイント。