【図解】ばねとフックの法則F=-kxの意味と単位、自然長について
1. フックの法則
皆さんは、ばねを引っ張ったり押し縮めたりしたことがありますか？そのとき、ばねが元の形に戻ろうとする力を感じたでしょう。この現象を説明するのが「フックの法則」です。
\[ F = -kx \]
ここで、
- \( F \) はバネや弾性体にかかる力（弾性力）
- \( k \) はバネ定数
- \( x \) はバネの変位（バネの自然長からの伸びや縮みの量）
1.1. 力のイメージ
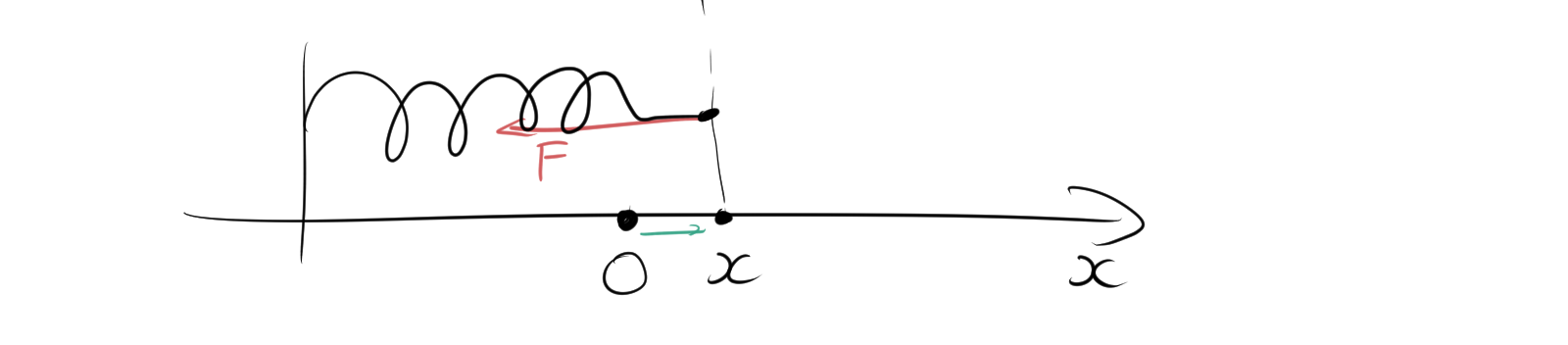
図のように、ばねを手で引っ張ると、力 \(F\) が加わります。このとき、ばねの自然長からの伸びた距離を \(x\) とします。
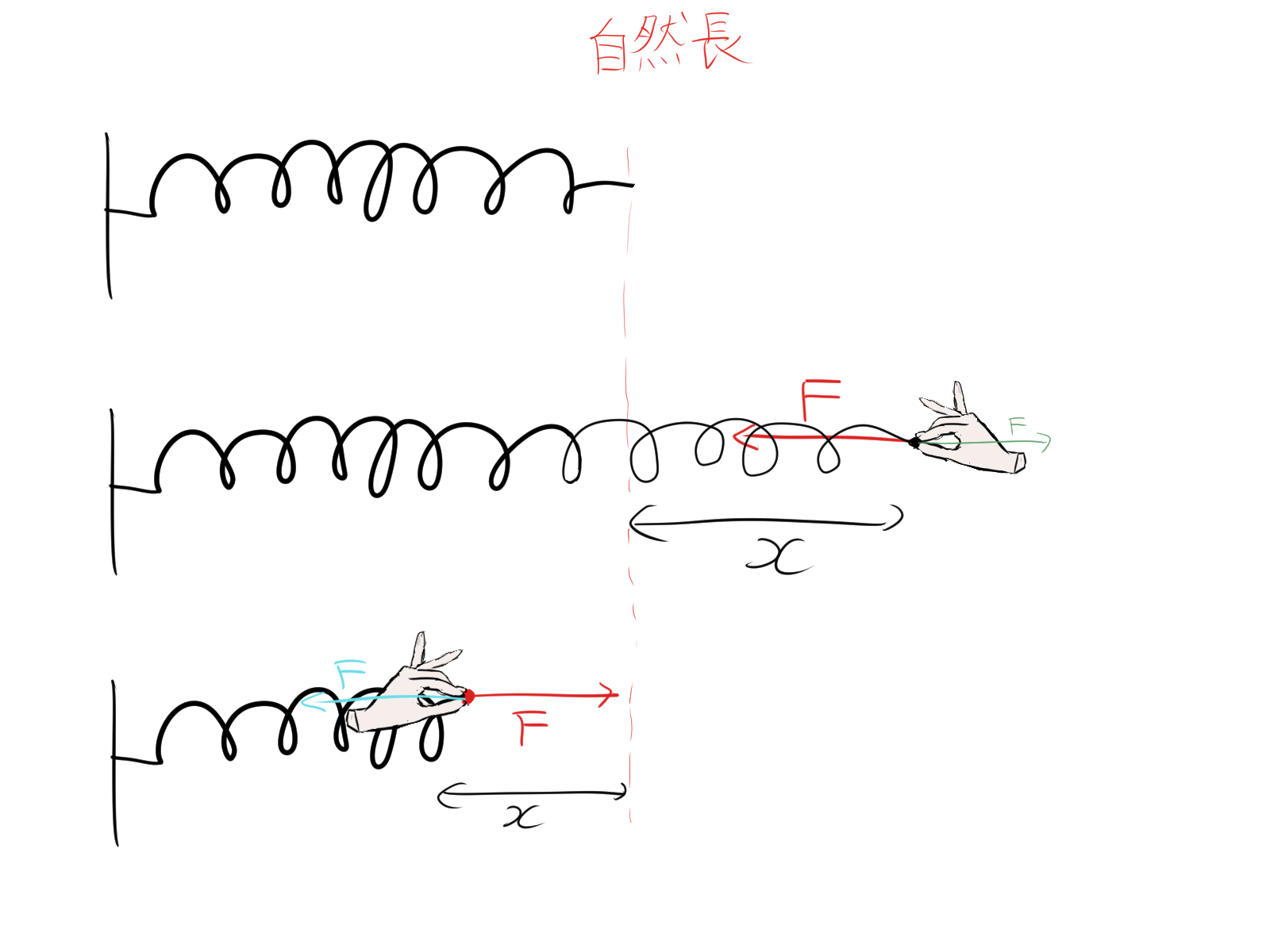このとき作用反作用の法則から、ばねにも力Fがかかる。
1.2. なぜマイナス
フックの法則は$F=-kx$でなく$F=kx$と説明される場合があります。これは、向きを考えずにスカラーのみを考えているからです。では、なぜベクトル（向きと力）を考えるとマイナスになるのか考えてみましょう。
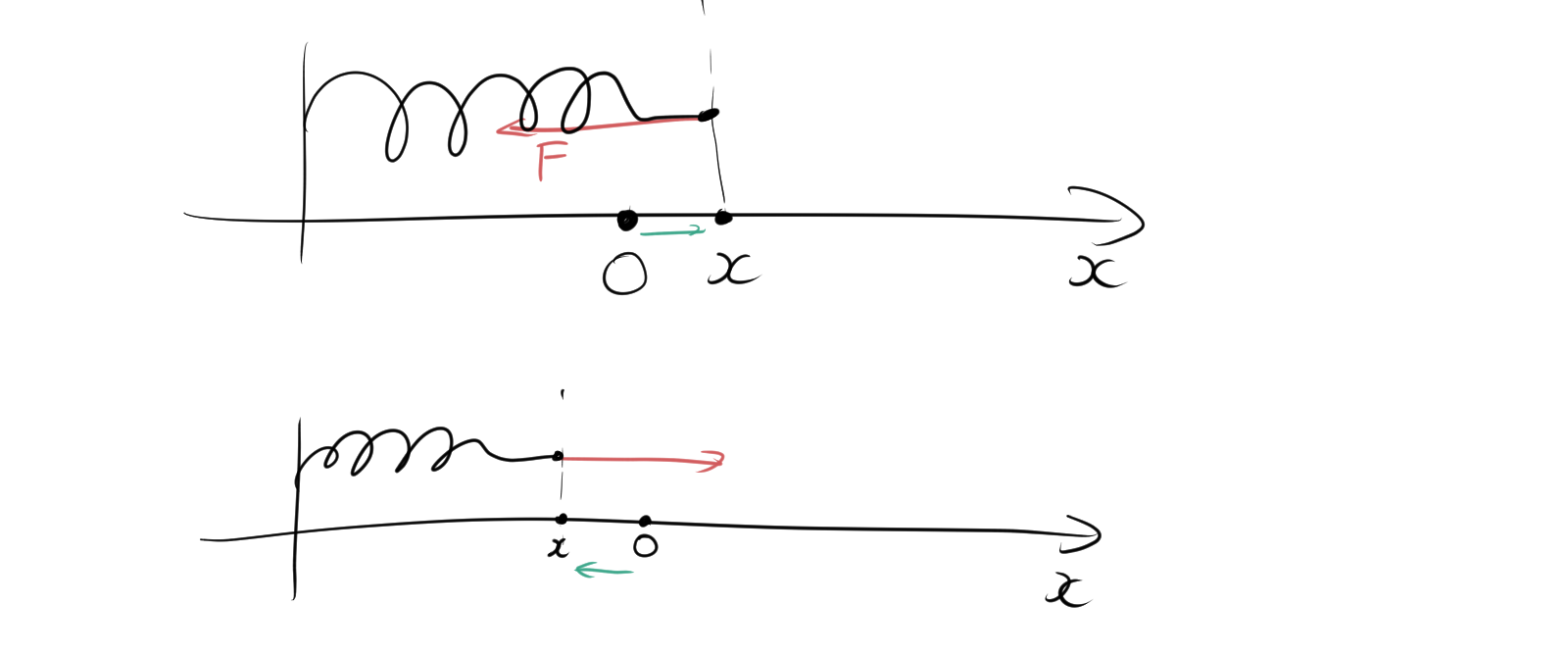
先ほど説明したように、作用反作用の法則によって、ばねに力 \(F\) が働いています。これに基づき、次の2つのケースが考えられます。自然長の位置をOとしてx軸上のばねにかかる力と変位xを考えます。
力と変位はベクトルであり、方向も重要な要素です。つまり、ばねが伸びる場合と縮む場合で力の符号が変わります。
1.2.1. 伸びるケース
ばねが伸びている場合、変位は \(x\) 軸と同じ方向であり、力 \(F\) はその反対方向に働きます。よって、次の式が成り立ちます。
\[ -F = kx \]
\[ F = -kx \]
1.2.2. 縮むケース
ばねが縮む場合は、力 \(F\) が \(x\) 軸と同じ方向に働き、変位はその逆方向に進みます。この場合の式は次のようになります。
\[ F = k(-x) \]
\[ F = -kx \]
どちらのケースでも、フックの法則 \(F = -kx\) に従い、力 \(F\) と変位 \(x\) は常に反対方向であることが示されています。
1.3. ばね定数とは？
ばね定数 \( k \) は、そのばねの硬さを表す値です。\( k \) の値が大きいほどばねは硬くなり、引っ張っても伸び縮みがしにくくなります。逆に、\( k \) の値が小さいとばねは柔らかくなり、少ない力で大きく伸び縮みするようになります。
式で考えてみると、フックの法則 \( F = -kx \) を変形することで、変位 \( x \) は次のように表せます。
\[ x = -\frac{F}{k} \]
この式からわかるように、力 \( F \) が一定であれば、ばね定数 \( k \) が大きいほど変位 \( x \) は小さくなり、ばねがあまり伸び縮みしないことがわかります。反対に、\( k \) が小さいと、ばねは大きく伸び縮みしやすくなります。]
1.4. 単位
ばね定数以外の単位は、
- \( F \) は力で、単位はニュートン (N) です。
- \( x \) はばねの変位で、単位はメートル (m) です。
したがって、$k=\frac{F}{x}$より、ばね定数 \( k \) の単位は次のように表されます。
\[ \frac{\text{ニュートン (N)}}{\text{メートル (m)}} = \text{N/m} \]
これにより、ばね定数の単位は ニュートン毎メートル (N/m) となります。この単位は、ばねを1メートル伸ばすために必要な力を表します。
運動方程式より、ニュートンの単位は$\text{kg} \cdot \text{m/s}^2$であるので、
\[ \frac{1 \, \text{N}}{1 \, \text{m}} = \frac{1 \, \text{kg} \cdot \text{m/s}^2}{\text{m}} \]
これにより、ばね定数 \( k \) の単位は次のようになります。
\[ \text{kg/s}^2 \]
2. 日常生活での例
2.1. アナログなタイプの体重計
体重を測るとき、ばねが縮みます。この縮み量から体重を計算しています。
2.2. 自動車のサスペンション
路面の凸凹を吸収するために、ばねが使われています。
2.3. 時計のゼンマイ
ばねの弾性を利用して動力を生み出しています。
