方べきの定理と逆の証明とベクトルを利用した証明、例題について
1. 方べきの定理
方べきの定理は、円とその外部または内部にある点との長さの関係を扱う定理です。方べきの定理は次の3パターンに分けられます。
$$ PA\times PB = PC \times PD $$
$$PA\times PB = PC \times PD $$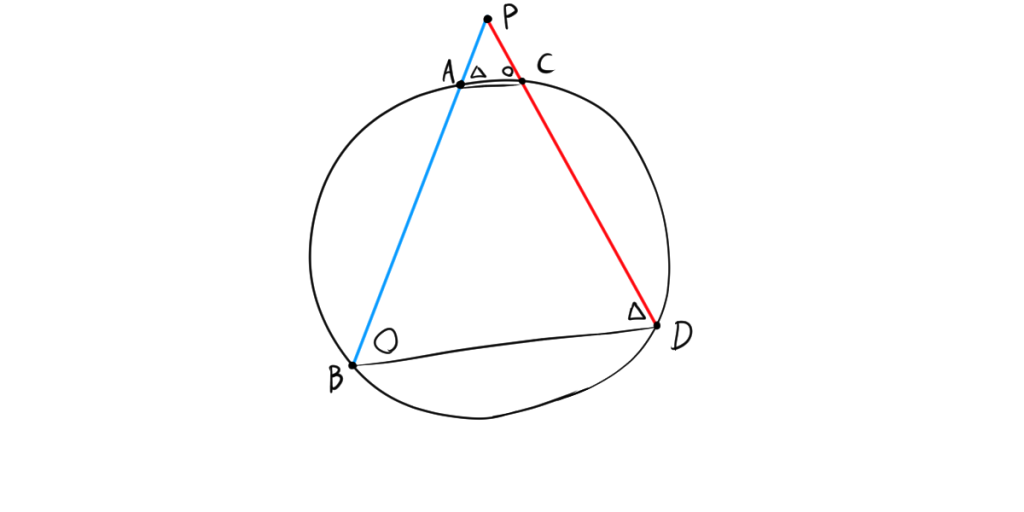
$$ PA\times PB = PT^2 $$
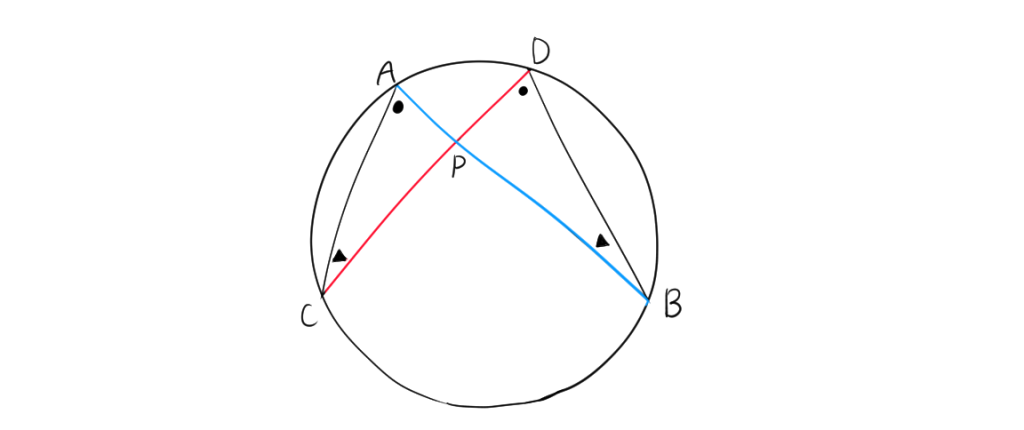
1.1. 方べきの定理のパターン1 (円の内部)
$$ PA\times PB = PC \times PD $$
円周角の定理より、
$$\angle CAB= \angle CDB $$
$$\angle ACD= \angle ABD $$
二つの角が等しいので、$\triangle ACP $と $\triangle DBP$は相似である。相似比より、
$$PA:PD=PC:PB$$
したがって、
$$ PA\times PB = PC \times PD $$
1.2. 方べきの定理のパターン2 (円の外部)
$$ PA\times PB = PC \times PD $$
四角形ABCDは円に内接する。したがって、
$$\angle PDB= \angle PAC $$
$$ \angle PBD=\angle PCA$$
二つの角が等しいので、$\triangle PAC $と $\triangle PBD$は相似である。相似比より、
$$PA:PC=PB:PD$$
したがって、
$$ PA\times PB = PC \times PD $$
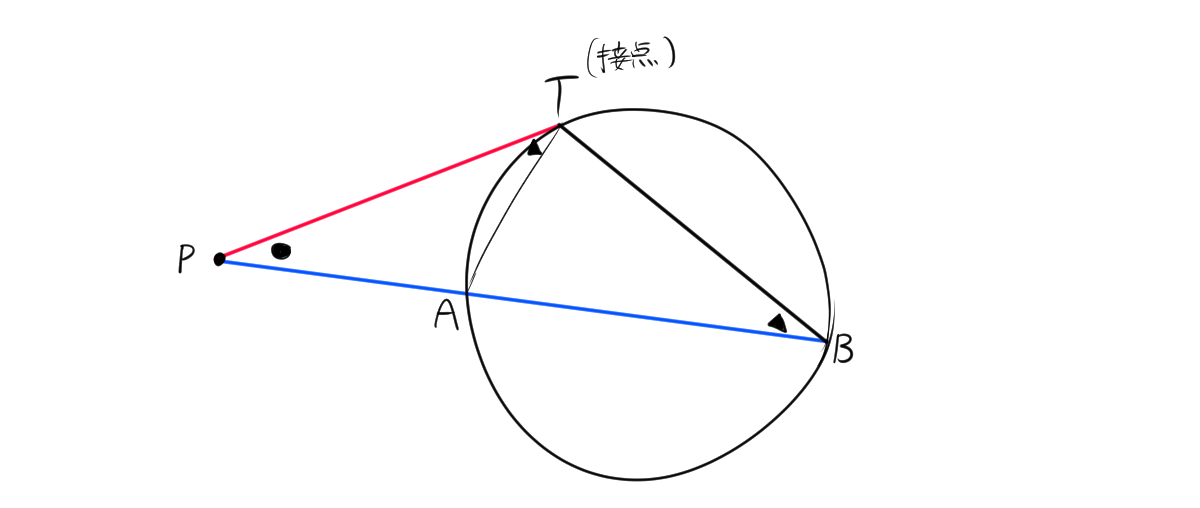
1.3. 方べきの定理のパターン3（接点）
$$ PA\times PB = PT^2 $$
接弦定理より、
$$\angle PTA= \angle PBT $$
点Pは共通の角であるので
$$\angle TPA= \angle BPT$$
二つの角が等しいので、$\triangle PTA $と $\triangle PBT$は相似である。相似比より、
$$PT:PA=PB:PT$$
したがって、
$$ PA\times PB = PT^2 $$
2. ベクトルを利用した証明
円の中心を \( O \) とし、半径を \( r \) とします。円の方程式は次のように表されます。円上の任意の点をXとすると、
\[ |\overrightarrow{OX}| = r\]
点 \( P \) は円の外部または内部にある任意の点で、2 本の直線が点 \( P \) を通り、円との交点を \( A \), \( B \), \( C \), \( D \) とします。また、各点 \( A \), \( B \), \( C \), \( D \)をベクトルで表現します。点 \( A \), \( B \), \( C \), \( D \) の位置ベクトルはそれぞれ次のように表されます。
\[ \overrightarrow{OA} = \overrightarrow{a}, \quad \overrightarrow{OB} = \overrightarrow{b}, \quad \overrightarrow{OC} = \overrightarrow{c}, \quad \overrightarrow{OD} = \overrightarrow{d} ,\quad \overrightarrow{OT} = \overrightarrow{t}\]
また、点 \( P \) の位置ベクトルを \( \overrightarrow{OP} = \overrightarrow{p} \) とします。
点$P,A,B$はどのパターンにおいても、共通の線分上に存在するので、実数$t$を利用して、
$$\overrightarrow{p} = t \overrightarrow{a} +(1-t) \overrightarrow{b}$$
ここで、
$$|\overrightarrow{PA}||\overrightarrow{PB}|=| \overrightarrow{a}- \overrightarrow{p}|| \overrightarrow{b}- \overrightarrow{p}|$$
先ほどの$\overrightarrow{p}$を代入すると、
$$\begin{align*}& | \overrightarrow{a}- t \overrightarrow{a} -(1-t) \overrightarrow{b}| | \overrightarrow{b}- t \overrightarrow{a} -(1-t) \overrightarrow{b}| \\ &= |(1 – t) \overrightarrow{a} – (1 – t) \overrightarrow{b}| \, | – t \overrightarrow{a} + t \overrightarrow{b}| \\ &= |1 – t| \, |t| \, |\overrightarrow{a} – \overrightarrow{b}| \\ &= |(1 – t)t| \, |\overrightarrow{a} – \overrightarrow{b}|^2 \\ &= |(1 – t)t| \left( |\overrightarrow{a}|^2 – 2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2 \right) \end{align*}$$
A,Bは円上の点であるので、
$$\begin{align*} &= |(1 – t)t| \left( 2r^2 – 2\overrightarrow{a} \cdot \overrightarrow{b} \right) \\ &= |(1 – t)t| \left( 2r^2 – 2r^2 \cos \angle AOB \right) \\ &= 2r^2 |(1 – t)t| \left( 1 – \cos \angle AOB \right) \\ &= 2r^2 |t(t-1)| \left( 1 – \cos \angle AOB \right) \end{align*}$$
一方で、
$$\begin{align*} \left| |\overrightarrow{p}|^2 – r^2 \right| &= \left| |t\overrightarrow{a} + (1-t) \overrightarrow{b}|^2 – r^2 \right| \\ &= \left| t^2|\overrightarrow{a} |^2 +2t(1-t) \overrightarrow{a}\cdot \overrightarrow{b} +(1-t)^2|\overrightarrow{b} |^2 – r^2 \right| \\ \end{align*}$$
A,Bは円上の点であるので、
$$\begin{align*}&= \left| t^2 r^2 + 2t(1 – t) \overrightarrow{a} \cdot \overrightarrow{b} +(1 – t)^2 r^2 – r^2 \right| \\ &=\left| t^2 r^2 + 2t(1 – t) \overrightarrow{a} \cdot \overrightarrow{b} +(t^2-2t+1)r^2 – r^2 \right| \\ &= \left| (2t^2-2t)r^2 – 2t(t – 1) \overrightarrow{a} \cdot \overrightarrow{b} \right| \\ &= \left| 2r^2 t(t – 1)(1 – \cos \angle AOB) \right| \\ &= 2r^2 |t(t – 1)| (1 – \cos \angle AOB)\end{align*}$$
したがって、
$$|\overrightarrow{PA}||\overrightarrow{PB}|=\left| |\overrightarrow{p}|^2 – r^2 \right|$$
同様にC,Dが円上に存在して、点Pと共通の線分に存在するので、
$$|\overrightarrow{PC}||\overrightarrow{PD}|=\left| |\overrightarrow{p}|^2 – r^2 \right|$$
このことから、
$$|\overrightarrow{PA}||\overrightarrow{PB}|=|\overrightarrow{PC}||\overrightarrow{PD}|$$
よって、方べきの定理は
$$ PA\times PB = PC \times PD $$
となる。CとDが同一である場合も成り立つ。
3. 方べきの定理の逆
3.1. パターン1・2の場合
パターン1と2の場合を一括で証明する。
$$ PA\times PB = PC \times PD $$が成り立つとき、
$$PA:PC=PB:PD$$
パターン1の場合は対頂角、パターン2の場合は共通な角より、
$$\angle APC = \angle BPD $$
したがって、2つの辺の比とその間の角が等しいので、$\triangle PAC $と $\triangle PBD$は相似である。
$$\angle PDB= \angle PAC $$
$$ \angle PBD=\angle PCA$$
となる。パターン1の場合は円周角の定理の逆、パターン2の場合は円に内接する四角形の性質より、A,B,C,Dは円周上に存在する。
3.2. パターン3の場合
$$ PA\times PB = PT^2 $$が成り立つとき、
$$PT:PA=PB:PT$$
点Pは共通の角であるので
$$\angle TPA= \angle BPT$$
2つの辺の比とその間の角が等しいので、$\triangle PTA $と $\triangle PBT$は相似である。
$$\angle PTA= \angle PBT $$
接弦定理の逆より、Tは接点であることがわかる。
4. 例題
方べきの定理より、次の関係が成立します。
\[ PA \times PB = PT^2 \]
ここで、接線の長さは \(PT = 8\)、また \(PA = 10\) です。したがって、
\[ 10 \times PB = 8^2 \]
\[ 10 \times PB = 64 \]
\[ PB = \frac{64}{10} = \frac{32}{5} \]
よって、もう一つの交点 \(B\) までの距離は \(PB = \dfrac{32}{5}\) です。
