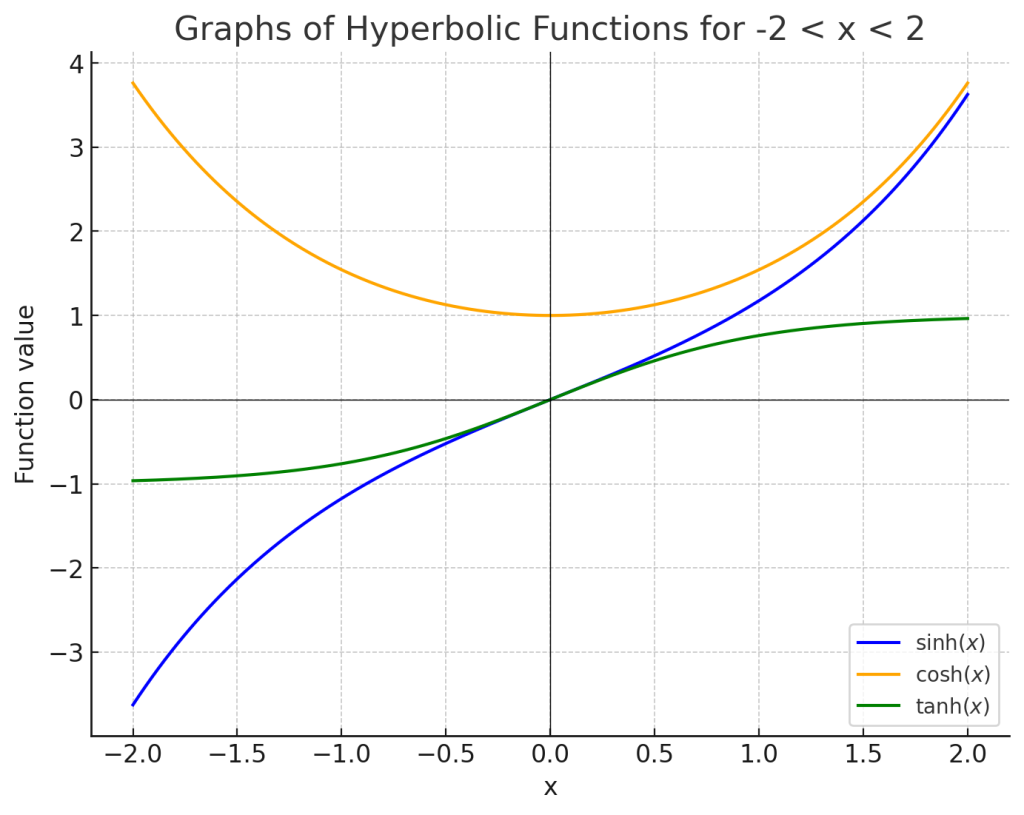
双曲線関数の定義・微分・関係式・性質・グラフ・例題について

1. 双曲線関数とは
\[ \sinh(x) = \frac{e^x – e^{-x}}{2} \]
\[ \cosh(x) = \frac{e^x + e^{-x}}{2} \]
\[ \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x – e^{-x}}{e^x + e^{-x}} \]
2. 双曲線関数の性質
2.1. 双曲線関数の性質1(三角関数と双曲線関数)
$$\large\cosh ix=\cos x$$
$$\large\cos ix=\cosh x$$
$$\large\sinh ix=\sin x$$
$$\large\sin ix=\sinh x$$
$i$は虚数単位とする。
オイラーの公式を使います。
$\begin{aligned}e^{ix}=\cos x+i\sin x\\ e^{-ix}=\cos x-i\sin x\end{aligned}$
より、それぞれの和と差で$\cos x$と$\sin x$を求めると
$\begin{aligned}\cos x=\dfrac{e^{-ix}+e^{ix}}{2}\\ \sin x=\dfrac{e^{ix}-e^{-ix}}{2i}\end{aligned}$
また、$\cosh x$と$\sinh x$は
$\begin{aligned}\cosh x=\dfrac{e^{x}+e^{-x}}{2}\\ \sinh x=\dfrac{e^{x}-e^{-x}}{2}\end{aligned}$
したがって、
$\cos ix=\dfrac{e^{x}+e^{-x}}{2}=\cosh x$
$\cosh ix=\dfrac{e^{ix}+e^{-ix}}{2}=\cos ix$
$\sin ix=\dfrac{e^{x}-e^{x}}{2i}=\dfrac{\left( e^{x}-e^{-x}\right) }{2}i=i\sinh x$
$\sinh ix=\dfrac{e^{ix}-e^{-ix}}{2}=i\sin x$
2.2. 双曲線関数の性質2(双曲線関数の関係式)
$$\large\cosh ^{2}x-\sinh ^{2}x=1$$
$$\large1-\tanh x^{2}=\dfrac{1}{\cosh ^{2}x}$$
まず、上の式を代入して求めると、
$\cosh ^{2}x-\sinh ^{2}x$
$=\dfrac{\left( e^{x}+e^{-x}\right) ^{2}}{4}-\dfrac{\left( e^{x}-e^{-x}\right) ^{2}}{4}$
$=\dfrac{e^{-2x}+2+e^{2x}}{4}-\dfrac{e^{-2x}-2+e^{2x}}{4}$
$=1$
いま求めた、この式の両辺を$\cosh ^{2}x$で割ると、$\tanh x=\dfrac{\sinh x}{\cosh x}$より、
$1-\dfrac{\sinh ^{2}x}{\cosh ^{2}x}=\dfrac{1}{\cosh ^{2}x}$
$1-\tanh ^{2}x=\dfrac{1}{\cosh ^{2}x}$
2.3. 双曲線関数の性質3
$$\large\cosh \left( -x\right) =\cosh x$$
$$\large\tanh \left( -x\right) =-\tanh x$$
$\sinh \left( -x\right)$について行うと、
$\sinh \left( -x\right)=\dfrac{e^{-x}-e^{x}}{2}$
$=\dfrac{-\left( e^{x}-e^{-x}\right) }{2}$
$=-\sinh x$
同様に、$\cosh \left( -x\right)$も行えばよい。また、$\tanh \left( -x\right)$はその結果を代入すればよい。
このことから、$\cosh x$は偶関数、$\sinh x$と$\tanh x$は奇関数であることが分かった。
2.4. 双曲線関数の性質4(微分)
\[ \frac{d}{dx} \sinh(x) = \cosh(x) \]
\[ \frac{d}{dx} \cosh(x) = \sinh(x) \]
\[ \frac{d}{dx} \tanh(x) = \frac{1}{\cosh^2(x)} \]
2.4.1. \(\sinh(x)\) の微分
\[ \sinh(x) = \frac{e^x – e^{-x}}{2} \]
この式を微分します。
\[ \frac{d}{dx} \sinh(x) = \frac{d}{dx} \left( \frac{e^x – e^{-x}}{2} \right) \]
\[= \frac{e^x + e^{-x}}{2} = \cosh(x) \]
したがって、
\[ \frac{d}{dx} \sinh(x) = \cosh(x) \]
2.4.2. \(\cosh(x)\) の微分
\[ \cosh(x) = \frac{e^x + e^{-x}}{2} \]
この式を微分します。
\[ \frac{d}{dx} \cosh(x) = \frac{d}{dx} \left( \frac{e^x + e^{-x}}{2} \right) \]
\[ = \frac{e^x – e^{-x}}{2} = \sinh(x) \]
したがって、
\[ \frac{d}{dx} \cosh(x) = \sinh(x) \]
2.4.3. \(\tanh(x)\) の微分
商の微分を使います。
\[ \frac{d}{dx} \tanh(x) = \frac{\frac{d}{dx} \sinh(x) \cdot \cosh(x) – \sinh(x) \cdot \frac{d}{dx} \cosh(x)}{\cosh^2(x)} \]
\(\frac{d}{dx} \sinh(x) = \cosh(x)\) と \(\frac{d}{dx} \cosh(x) = \sinh(x)\) より、
\[ \frac{d}{dx} \tanh(x) = \frac{\cosh^2(x) – \sinh^2(x)}{\cosh^2(x)} \]
ここで、双曲線関数の恒等式 \(\cosh^2(x) – \sinh^2(x) = 1\) を使うと、
\[ \frac{d}{dx} \tanh(x) = \frac{1}{\cosh^2(x)} \]
3. 例題
3.1. 例題1: 双曲線関数の基本的な計算
- \(\sinh(x) = \frac{e^x – e^{-x}}{2}\)
- \(\cosh(x) = \frac{e^x + e^{-x}}{2}\)
- \(\tanh(x) = \frac{\sinh(x)}{\cosh(x)}\)
\(x = 1\) のときの \(\sinh(x)\), \(\cosh(x)\), \(\tanh(x)\) を計算してください。
\[ \sinh(1) = \frac{e^1 – e^{-1}}{2} \approx 1.175 \]
\[ \cosh(1) = \frac{e^1 + e^{-1}}{2} \approx 1.543 \]
\[ \tanh(1) = \frac{e^1 – e^{-1}}{e^1 + e^{-1}}\approx 0.761 \]
3.2. 例題2: 双曲線関数を用いた方程式の解
\[ \cosh(x) = 3 \]
\(\cosh(x) = \frac{e^x + e^{-x}}{2}\) なので、次のような方程式を得ます。
\[ \frac{e^x + e^{-x}}{2} = 3 \]
両辺を2倍して、次のようになります。
\[ e^x + e^{-x} = 6 \]
これを \(y = e^x\) と置き換えると、次の二次方程式になります。
\[ y + \frac{1}{y} = 6 \]
両辺に \(y\) をかけて整理します。
\[ y^2 – 6y + 1 = 0 \]
二次方程式の解の公式を使うと、
\[ y = \frac{6 \pm \sqrt{36 – 4}}{2} = 3 \pm 2\sqrt{2} \]
したがって、
\[ e^x = 3 + 2\sqrt{2} \quad \text{または} \quad e^x = 3 – 2\sqrt{2} \]
これを両辺自然対数を取って、解は次の通りです。
\[ x = \ln(3 + 2\sqrt{2}),\ln(3 – 2\sqrt{2}) \]