双曲線関数の逆関数

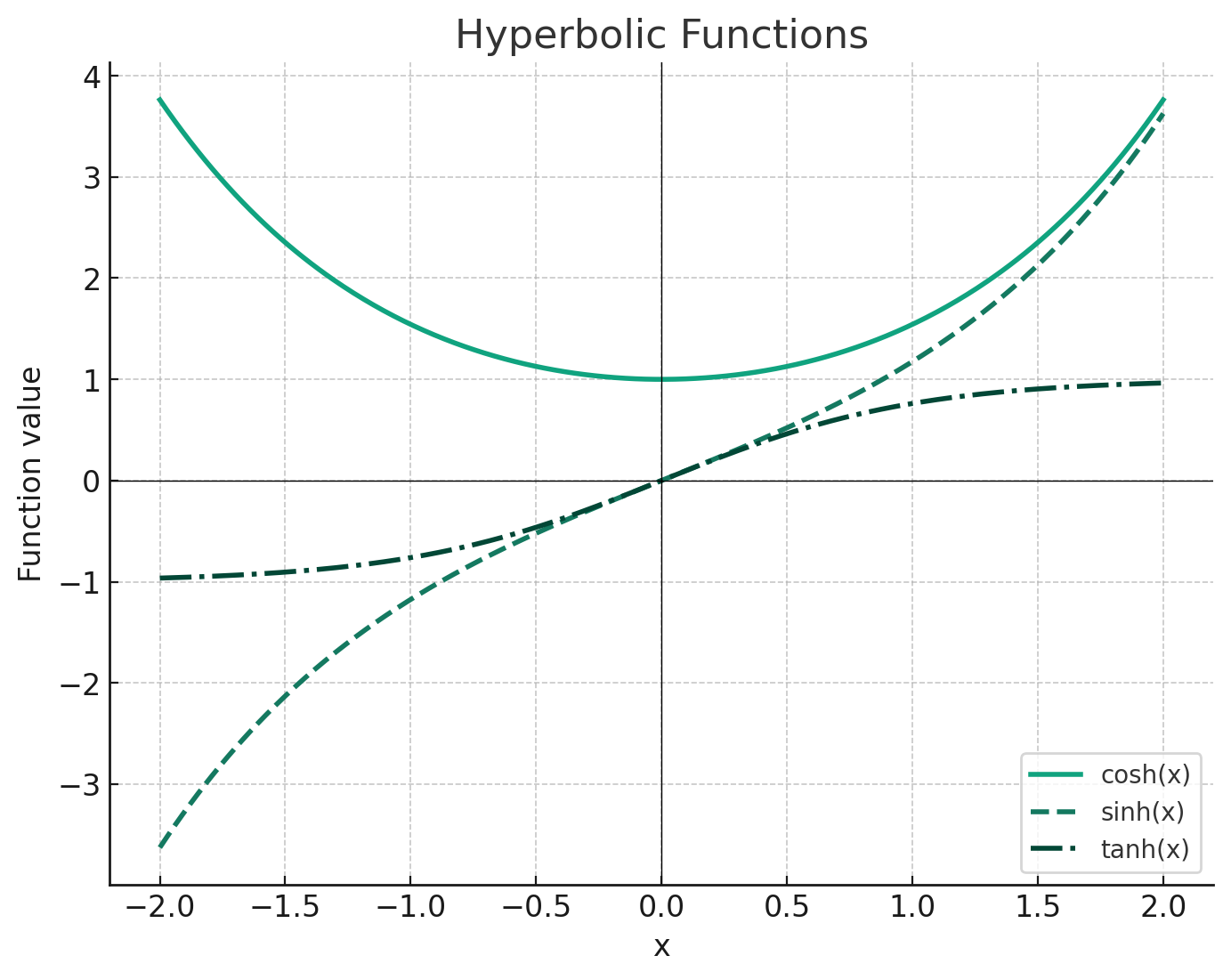
1. 双曲線関数とは

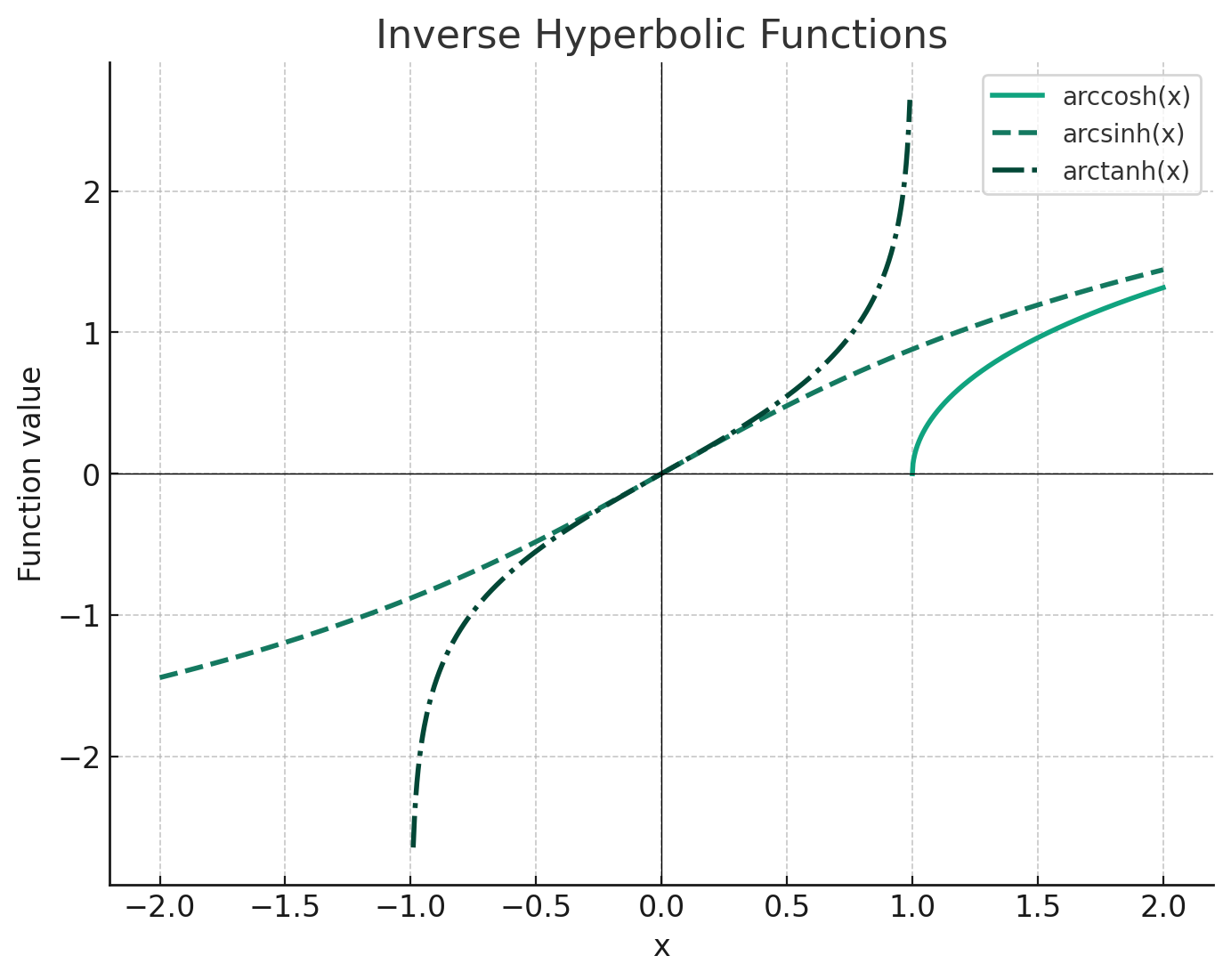
2. 双曲線関数の逆関数

 

2.1. 1. $\sinh^{-1} x = \log(x + \sqrt{x^2 + 1})$ の証明

関数 $y = \sinh x = \frac{e^x – e^{-x}}{2}$ の逆関数を考えるため、$y = \sinh^{-1} x$ と置いて、$x = \sinh y$ となります。これを $y$ について解く。

$ x = \frac{e^y – e^{-y}}{2} $

これを $e^y$ について解くと、

$ e^y – e^{-y} = 2x \\ e^y – \frac{1}{e^y} = 2x \\ e^{2y} – 2xe^y – 1 = 0 $

これは $e^y$ についての二次方程式で、解の公式を用いて解く。

$ e^y = \dfrac{2x \pm \sqrt{(2x)^2 + 4}}{2}  \\ = x \pm \sqrt{x^2 + 1} $

$e^y>0$ より、正の符号の解を選びます。よって、

$ y = \log(x + \sqrt{x^2 + 1}) $

このため、$\sinh^{-1} x$ は、

$ \sinh^{-1} x = \log(x + \sqrt{x^2 + 1}) $

2.2.  2. $\cosh^{-1} x = \log(x + \sqrt{x^2 – 1})$ $(x > 1)$ の証明

関数 $y = \cosh x = \frac{e^x + e^{-x}}{2}$ の逆関数を考えるため、$y = \cosh^{-1} x$ と置いて、$x = \cosh y$ となります。これを $y$ について解く。

ただし、$ \cosh x$ は$[0,\infty) \to [1,\infty)$ であるから$ \cosh^{-1} x$ の定義域は$[1,\infty) \to[0,\infty) $ となる。

$ x = \frac{e^y + e^{-y}}{2} $

これを $e^y$ について解くと：

$ e^y + e^{-y} = 2x \\ e^{2y} – 2xe^y + 1 = 0 $

これも $e^y$ についての二次方程式で、解の公式を用いて解く。

$ e^y = \frac{2x \pm \sqrt{(2x)^2 – 4}}{2} = x \pm \sqrt{x^2 – 1} $

$e^y > 0$ のため、正の符号の解を選びます。よって、

$ y = \log(x + \sqrt{x^2 – 1}) $

このため、$\cosh^{-1} x$ は、

$ \cosh^{-1} x = \log(x + \sqrt{x^2 – 1}) $

2.3. 3. $\tanh^{-1} x = \frac{1}{2} \log\left(\frac{1+x}{1-x}\right)$ $(-1 < x < 1)$ の証明

関数 $y = \tanh x = \frac{e^x – e^{-x}}{e^x + e^{-x}}$ の逆関数を考えるため、$y = \tanh^{-1} x$ と置いて、$x = \tanh y$ となります。これを $y$ について解く。ただし、$ \tanh x$ は$\mathbb{R} \to (-1,1)$ であるから$ \tanh^{-1} x$ の定義域は$ (-1,1)\to\mathbb{R} $ となる。

$ x = \displaystyle\frac{e^y – e^{-y}}{e^y + e^{-y}} $

これを $e^y$ について解くと

$ x(e^y + e^{-y}) = e^y – e^{-y} \\ xe^y + xe^{-y} = e^y – e^{-y} \\ (e^y – xe^y) – (xe^{-y} – e^{-y}) = 0 \\ e^y(1 – x) = e^{-y}(1 + x) \\ e^{2y} = \displaystyle\frac{1+x}{1-x} $

$-1<x<1$ より、$\displaystyle\frac{1+x}{1-x}>0$であるから、両辺の自然対数を取ると、

$ 2y = \displaystyle\log\left(\frac{1+x}{1-x}\right) $

$ y = \displaystyle\frac{1}{2} \log\left(\frac{1+x}{1-x}\right) $

このため、$\tanh^{-1} x$ は、

$\tanh^{-1} x = \displaystyle\frac{1}{2} \log\left(\frac{1+x}{1-x}\right)$