線形写像fの像（Imf）と部分空間について！Imfを理解しよう

はるか

今日は、線形写像fの像について話そう。

ふゅか

まず、像って何かを簡単に説明するね！

1. Im fの定義

はるか

像は $f(\mathbf{x})$の集合。

2. ImfはWの部分集合

\( \text{Im}(f) \) は、線形写像 \( f \) によって \( V \) から \( W \) への変換された場合、$\text{Im}(f)$は$W$の部分集合になります。

ふゅか

つまり、像は$W$の中に収まるってことだね！

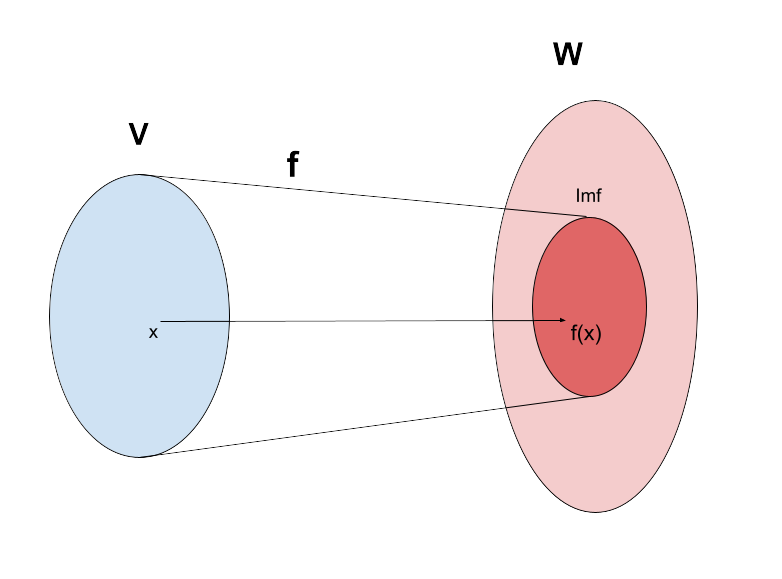
2.1. Wの部分集合であることの証明

以下に、それぞれの条件について証明します。

2.2. 加法

任意の \( \mathbf{u}, \mathbf{v} \in \text{Im}(f) \) を取りましょう。これらは、\( \mathbf{u} = f(\mathbf{a}) \) および \( \mathbf{v} = f(\mathbf{b}) \) という形で表されます。ただし、\( \mathbf{a}, \mathbf{b} \in V \) です。

線形写像の性質により、$f(\mathbf{x}) + f(\mathbf{y}) = f(\mathbf{x} + \mathbf{y})$であるから、

\[ \mathbf{u} + \mathbf{v} = f(\mathbf{a}) + f(\mathbf{b}) = f(\mathbf{a} + \mathbf{b}) \]

ここで \( \mathbf{a} + \mathbf{b} \in V \) 、\( f(\mathbf{a} + \mathbf{b} )\in W \)で、\( \mathbf{u} + \mathbf{v} \in \text{Im}(f) \) です。したがって、加法に対して閉じています。

2.3. スカラー倍

任意の \( \mathbf{u} \in \text{Im}(f) \) とスカラー \( c \in \mathbb{R} \) を取りましょう。\( \mathbf{u} = f(\mathbf{a}) \) と表されます。ただし、\( \mathbf{a} \in V \) です。

線形写像の性質の$ c\mathbf{x} = f(c \mathbf{x})$により、

\[ c \mathbf{u} = c f(\mathbf{a}) = f(c \mathbf{a}) \]

ここで \( c \mathbf{a} \in V \)、\( f(c\mathbf{a})\in W \) で、\( c \mathbf{u} \in \text{Im}(f) \) です。したがって、スカラー倍に対して閉じています。

以上により、像 \( \text{Im}(f) \) が \( W \) の部分空間であることが示されました。

はるか

以上から、像 が $W $の部分空間であることが示された。

ふゅか

うん、これで線形写像の像が部分空間になる理由がわかったね！しっかり理解できたよ☆