【図形】三角形の内心の意味と性質、例題について
1. 内心
内心とは、三角形の内角の二等分線が交わる一点です。内心は英語でinner centerであり、頭文字からIが使われる。
2. 内心の性質
2.1. 角の二等分線が一点で交わる
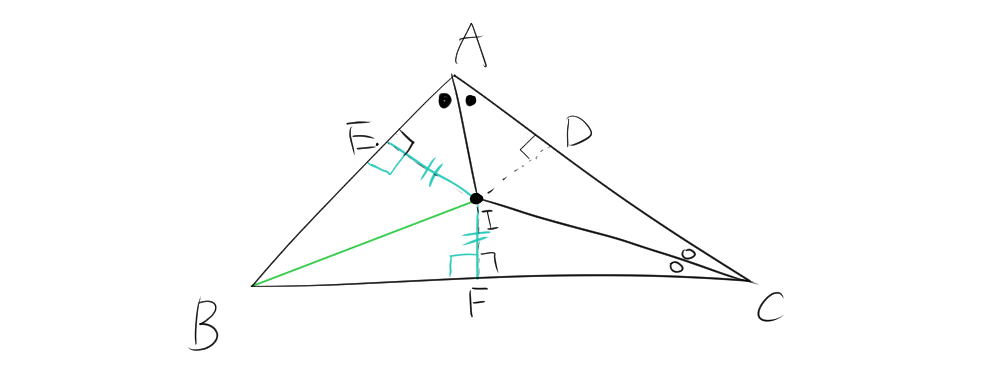
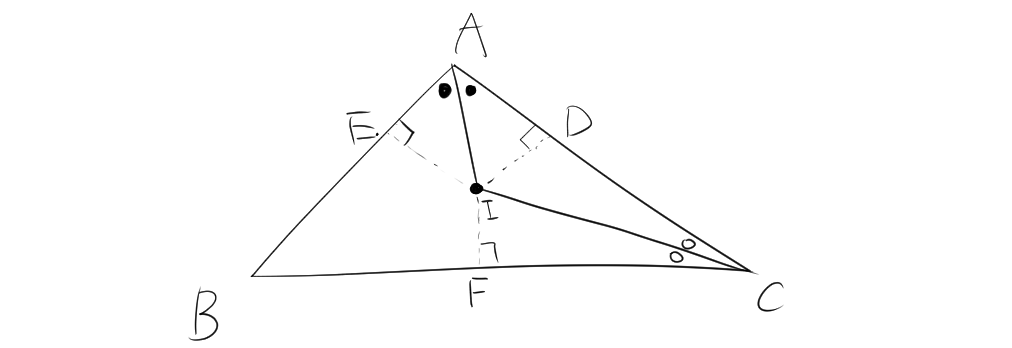
$\angle A$と$\angle C$の二等分線の交点$I$を考えます。交点$I$から垂線を下したとき、$AC$、$BC$、$AB$と垂線の交点を$D$、$F$、$E$とする。
$\triangle AIE$と$\triangle AID$について着目する。二等分線から
$$\angle IAE = \angle IAD $$
垂線を引いたことから
$$\angle AEI= \angle ADI=90 ^{\circ}$$
となる。したがって、直角三角形の合同条件より、直角三角形の斜辺と鋭角が等しいので、$\triangle AIE$と$\triangle AID$は合同である。合同な三角形の辺の長さは等しいので、EI=IDであることがわかる。
同様に考えると、$\triangle CIF$と$\triangle CID$は合同である。合同な三角形の辺の長さは等しいので、ID=IFである。
したがって、$EI=ID=IF$となる。
次に、三角形BIEとBIFについて着目する。
先ほど、IE=IFであることを求めたので、直角三角形の斜辺とその他の辺が等しいので、三角形BIEとBIFは合同である。合同な三角形の角は等しいので、
$$\angle IBE = \angle IBF $$
したがって、$\angle B$はBIは二等分線になる。
2.2. 内接円の中心
先ほどの結果から、$EI=ID=IF$、$90^{\circ}$で接するので、Iは内接円の中心である。
2.3. 三角形の面積
$$S=\dfrac{r}{2}(a+b+c)$$
となる。
3. 例題
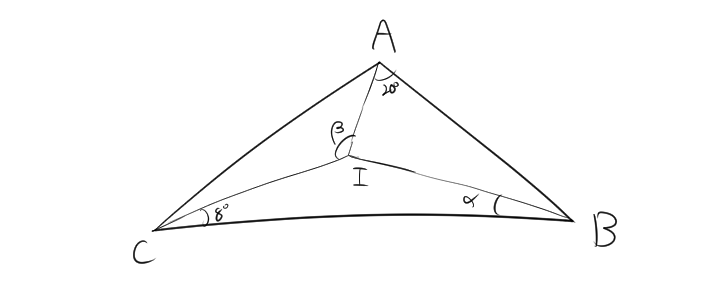
$IA,IB,IC$は二等分線であるので、
$$\angle A=40^{\circ},\angle B=2\alpha , \angle A=16^{\circ}$$
したがって、三角形の内角の和は$180^{\circ}$であるので
\[ \begin{aligned} 40^{\circ} + 2\alpha + 16^{\circ} &= 180^{\circ} \\ 2\alpha + 56^{\circ} &= 180^{\circ} \\ 2\alpha &= 124^{\circ} \\ \alpha &= 62^{\circ} \end{aligned} \]
次に、三角形ABIについて着目する。二等分線の性質から、
\[ \begin{aligned} \beta + 20^{\circ} + 8^{\circ} &= 180^{\circ} \\ \beta + 28^{\circ} &= 180^{\circ} \\ \beta &= 152^{\circ} \end{aligned} \]
