因数定理と重解、微分の関係・具体例について
1. 因数定理と微分と重解
1.1. 因数定理とは
因数定理とは、多項式 \( P(x) \) が \( (x – r) \) を因数として持つ場合、その多項式の値 \( P(r) = 0 \) となる、という定理です。つまり、\( P(x) = 0 \) の解 \( r \) を見つけた場合、\( (x – r) \) は \( P(x) \) の因数となります。
1.2. 因数定理と重解
重解（重根）とは、同じ解が複数回現れる場合を指します。例えば、方程式 \( P(x) = 0 \) の解が \( r \) であり、さらにその解が重複して現れるとき、これを重解と呼びます。例えば、多項式 \( P(x) \) が \( (x – r)^k \) の形を持つとき、\( r \) は重解となります。
2. 微分と重解について
\( f(r) = f'(r) = f^{(2)}(r) = \cdots = f^{(k-1)}(r) = 0 \) かつ \( f^{(k)}(r) \neq 0 \) のとき、\( (x – r)^k \) を因数に持ちます。このとき、
$$ (x – r)^kを因数に持つ \Leftrightarrow f(r) = f'(r) = f^{(2)}(r) = \cdots = f^{(k-1)}(r) = 0 $$
2.1. 証明1
まず、$\Rightarrow$を証明します。多項式 \( f(x) \) が \( r \) に重解を持つと仮定します。すると、\( f(x) \) は次のように表されます。
\[ f(x) = (x – r)^k g(x) \]
ここで、\( g(x) \) は \( g(r) \neq 0 \) を満たす多項式です。微分を繰り返します。まず、\( f(x) \) の 1 階微分を求めると、積の微分法則より、
\[ f'(x) = k(x – r)^{k-1} g(x) + (x – r)^k g'(x) \]
となります。\( r \) を代入すると、\( f(r) = 0 \)、\( f'(r) = 0 \) が成り立ちます。
k-1階微分まで、繰り返すと$ f(r) = f'(r) = f^{(2)}(r) = \cdots = f^{(k-1)}(r) = 0 $が成り立つ。
最後に \( k \) 次微分では、\( (x – r)^k \) の項が消えてしまい、\( g(x) \) が残るため。
\[ f^{(k)}(r) = k! g(r) \]
となり、\( g(r) \neq 0 \) なので \( f^{(k)}(r) \neq 0 \) です。
次に、$\Leftarrow$を証明します。
$f(r) = f'(r) = f^{(2)}(r) = \cdots = f^{(k-1)}(r) = 0$ならば、 $(x – r)^k$を因数に持つということを数学的帰納法を利用して証明する。
k=1のとき、因数定理より、$f(r)=0$のとき、$x-r$の因数を持つため成り立つ。
k=nのとき、
$f(r) = f'(r) = f^{(2)}(r) = \cdots = f^{(n-1)}(r) = 0$ならば、多項式$f(x)$は\( (x – r)^n \)の因数を持つと仮定する。したがって、$g(x)$を商とすると、
$$f(x)=(x-r)^ng(x)$$
とあらわすことができる。
$k=n+1$のときを考える。
仮定より、$f(x)$を$n階微分$したときの$f^{n}(r)$は
$$f^{n}(r) = n! g(r)$$
となる。$f^{n}(r) = 0$のとき、
$$f^{n}(r) = n! g(r) = 0$$
したがって$g(r)=0$となるので、$g(x)$は$x-r$を因数に持つ。よって、$g(x)=(x-r)h(x)$と置くと、
$$\begin{align*} f(x)&=(x-r)^n(x-r)h(x) \\ &=(x-r)^{n+1}h(x) \end{align*}$$
したがって、$f(r) = f'(r) = f^{(2)}(r) = \cdots = f^{(n-1)}(r)=f^{n}(r) = 0$ならば、多項式$f(x)$は\( (x – r)^n \)の因数を持つため、$k=n+1$の時も成り立つ。
したがって、数学的帰納法より、 $f(r) = f'(r) = f^{(2)}(r) = \cdots = f^{(k-1)}(r) = 0$ならば、 $(x – r)^k$を因数に持つことが証明された。
2.2. 証明2
任意のn次の多項式は$\sum b_i x^i$として利用されますが、今回の証明は$\sum c_i(x-a)^i$を任意の多項式と置きます。そこで、次の性質を利用します。
最初に、\( x \) を \( (x – a) + a \) という形に変数変換します。この置換を使って、各項 \( b_i x^i \) を次のように書き換えることができます。
\[ b_i x^i = b_i \left( (x – a) + a \right)^i \]
次に、この式の \( \left( (x – a) + a \right)^i \) の部分を展開するために二項定理より
\[ \left( (x – a) + a \right)^i = \sum_{j=0}^{i} {}_i\mathrm{C}_j \cdot (x – a)^j \cdot a^{i – j} \]
ここで、\( i \mathrm{C} j \) は二項係数を表しています。この式は、\( (x – a) \) のべき乗 \( (x – a)^j \) と \( a \) のべき乗 \( a^{i – j} \) の積として展開されており、それぞれの係数は二項係数 \( _i \mathrm{C} _j \) によって決まります。
この操作をすべての \( i \) に対して行います。つまり、左辺の多項式全体に対して同じ変形を適用します。
\[ \sum_{i=0}^{n} b_i x^i = \sum_{i=0}^{n} b_i \sum_{j=0}^{i} {}_i \mathrm{C}_j \cdot (x – a)^j \cdot a^{i – j} \]
整理すると、
\[ \sum_{i=0}^{n} b_i x^i = \sum_{i=0}^{n} b_i \sum_{j=0}^{i} {}_i \mathrm{C}_j \cdot (x – a)^j \cdot a^{i – j} \]
したがって、$(x-a)^i$の係数を$c_i$と置くと、
\[ \sum_{i=0}^{n} b_i x^i =\sum_{i=0}^{n} c_i(x-a)^i \]
$\sum_{i=0}^{n} b_i \sum_{j=0}^{i} {}_i \mathrm{C}_j \cdot (x – a)^j \cdot a^{i – j}$の係数のイメージは次のようになります。
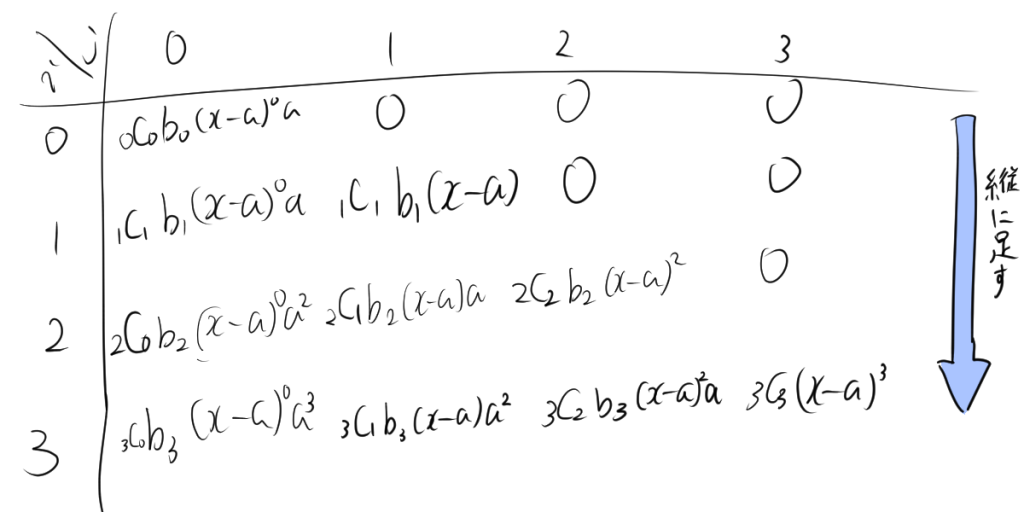イメージの様に縦に足していくことで、それぞれの項を計算することができます。
まず、多項式 \( f(x) \) を \( (x – a)^k \) で割ったとき、得られる商を \( Q(x) \)、余りを \( R(x) \) とします。このとき、余り \( R(x) \) は \( k-1 \) 次以下の多項式になります。
\[ R(x) = \sum_{i=0}^{k-1} b_i (x – a)^i \]
多項式 \( f(x) \) を商 \( Q(x) \) と余り \( R(x) \) を使って、
\[ f(x) = (x – a)^k Q(x) + \sum_{i=0}^{k-1} b_i (x – a)^i \]
0<s<k とすると、この式の両辺を \( s \) 階微分し、その結果に \( x = a \) を代入します。そして、これに \( x = a \) を代入すると、次の式が得られます。
\[ f^{(s)}(a) = s! \cdot b_s \]
つまり、\( f(x) \) の \( s \) 回微分したときの \( a \) における値を使って、対応する余りの係数 \( b_s \) を特定できることがわかる。
次に、多項式 \( f(x) \) が \( (x – a)^k \) で割り切れるための条件について考えます。割り切れるというのは、余りがゼロになることを意味します。つまり、すべての余りの係数 \( b_0, b_1, \dots, b_{k-1} \) は0になります。
\[ b_0 = b_1 = \dots = b_{k-1} = 0 \]
さらに、これを微分の視点から見ると、
\[ f(a) = f'(a) = \dots = f^{(k-1)}(a) = 0 \]
3. 重解と微分の例
多項式 \( f(x) = (x – 2)^3(x – 1) \) を考えます。この多項式には \( (x – 2)^3 \) という因数が含まれており、\( k = 3 \)、つまり \( f(x) \) の \( r = 2 \) での値とその 2 階までの導関数が 0 であることを確認します。
まず、\( f(x) = (x – 2)^3(x – 1) \) を展開します。
\[ \begin{align*} f(x) &= (x – 2)^3(x – 1) \\ &= (x^3 – 6x^2 + 12x – 8)(x – 1) \\ &= x^4 – 7x^3 + 18x^2 – 20x + 8 \\ \end{align*}\]
\( f(2) \) を計算します。
\[ f(2) = 2^4 – 7 \cdot 2^3 + 18 \cdot 2^2 – 20 \cdot 2 + 8 = 16 – 56 + 72 – 40 + 8 = 0 \]
\( f'(x) \) を計算し、\( f'(2) \) を確認します。
\( f'(x) \) を計算すると、
\[ f'(x) = 4x^3 – 21x^2 + 36x – 20 \]
\( f'(2) \) を計算すると、
\[ f'(2) = 4 \cdot 2^3 – 21 \cdot 2^2 + 36 \cdot 2 – 20 = 32 – 84 + 72 – 20 = 0 \]
\( f”(x) \) を計算し、\( f”(2) \) を確認します。
\( f”(x) \) を計算すると、
\[ f”(x) = 12x^2 – 42x + 36 \]
\(f”(2) \) を計算すると、
\[ f”(2) = 12 \cdot 2^2 – 42 \cdot 2 + 36 = 48 – 84 + 36 = 0 \]
したがって、\( f(2) = f'(2) = f”(2) = 0 \) であることが確認できました。さらに、\( (x – 2)^3 \) という因数を持つので、条件が満たされています。
