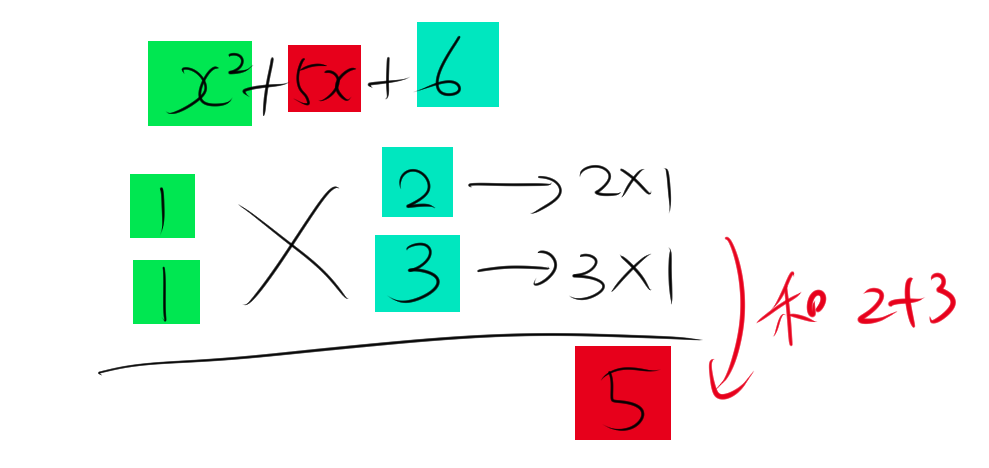因数分解の意味・基本的なパターン・例題について

1. 因数分解
因数分解は、数や式をいくつかの因数に分ける手法です。特に数学の方程式や多項式を簡略化したり解を見つけたりする際に使われます。ここでは、因数分解の基本的な考え方や具体的な手法について説明します。
1.1. 因数分解の基本
因数分解の基本は、共通の因数を見つけて取り出すことです。例えば、次のような式を見てみましょう。
\[ 6x + 12 \]
この式の各項に共通している因数は「6」です。そこで、6を外に出して因数分解を行います。
\[ 6x + 12 = 6(x + 2) \]
このように、式を共通因数でくくり出すことが因数分解の基本です。「共通の因数」とは、複数の項の中で、全ての項に共通して現れる因数(かけ算の部分)を指します。言い換えると、すべての項に含まれていて、各項から取り出すことができる数や文字です。
2. 因数分解の代表的なパターン
次に、代表的な因数分解のパターンをいくつか紹介します。
2.1. ① 共通因数をくくり出す
これは最も基本的な方法です。共通の因数を式全体から取り出し、残りをカッコでくくります。
\[ 4x^2 – 8x = 4x(x – 2) \] 「4x」を共通因数として取り出しました。
2.2. ② 公式を使った因数分解
いくつかの因数分解の公式があります。これらを覚えておくと、式を素早く分解できます。
\[ \begin{align*} (a+b)^2 &= a^2 + 2ab + b^2 \\ (a-b)^2 &= a^2 – 2ab + b^2 \\ (a+b)(a-b) &= a^2 – b^2 \\ (a+b)^3 &= a^3 + 3a^2b + 3ab^2 + b^3 \\ (a-b)^3 &= a^3 – 3a^2b + 3ab^2 – b^3 \\ (a+b)(a^2-ab+b^2) &= a^3 + b^3 \\ (a-b)(a^2+ab+b^2) &= a^3 – b^3 \\ (a+b+c)^2 &= a^2 + b^2 + c^2 + 2ab + 2bc + 2ca \\ (a+b+c)(a^2+b^2+c^2-ab-bc-ca) &= a^3 + b^3 + c^3 – 3abc \end{align*} \]
2.3. ③ 因数分解の応用(たすき掛け)
二次式の因数分解では「たすき掛け」がよく使われます。例えば、次のような式を考えます。
\[ x^2 + 5x + 6 \]
たすき掛けでは、係数「5」と「6」に注目します。「6」を分解して和が「5」になる組み合わせを見つけます。
- まず「6」を素因数分解して \( (2, 3) \) というペアを得ます。
- \( 2 + 3 = 5 \) となるので、このペアを使って次のように分解します。
\[ x^2 + 5x + 6 = (x + 2)(x + 3) \]
2.4. 因数分解の手順
因数分解の問題を解くときには、次の手順を意識して進めましょう。
- 共通因数を見つける:まずは全ての項に共通する因数を探します。
- 因数分解の公式が使えるか確認する:平方の和や完全平方式などの公式が使える場合は、適用します。
- 使える公式がない場合は、たすき掛けやその他の方法で因数分解を試みます。
3. 練習問題
因数分解を実際に練習してみましょう。
3.1. 問題 1
\[ x^2 – 16 \]
これは平方の差の形なので、次のように因数分解できます。
\[ x^2 – 16 = (x – 4)(x + 4) \]
3.2. 問題 2
\[ x^2 + 4x + 4 \]
これは平方の形なので、次のように因数分解できます。
\[ x^2 + 4x + 4 = (x + 2)^2 \]
3.3. 問題 3
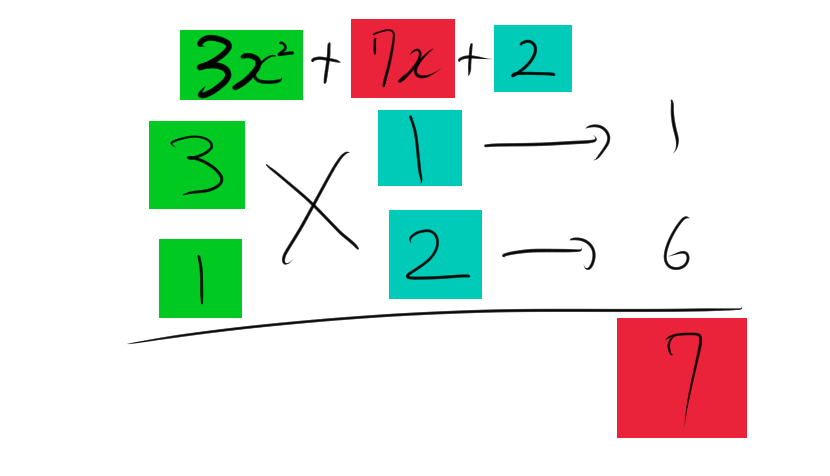
\[ 3x^2 + 7x + 2 \]
たすき掛けを使って因数分解すると、次のようになります。
\[ 3x^2 + 7x + 2 = (3x + 1)(x + 2) \]