区分求積法の定義・導出・計算問題・対数について
1. 区分求積法とは
区分求積法は、面積を複数の小さな長方形に分割し、それぞれの面積を求めて足し合わせることで全体の面積を求めます。0から1の範囲で次のような数式で表すことができます。
$$\int_0^1 f(x) \, dx = \lim_{n\to \infty}\sum_{k=0}^{n-1}\frac{1}{n}f \left(\frac{k}{n}\right)$$
1.1. 導出
0から1の範囲の次のような赤色の部分の図形の面積を求めたいとします。
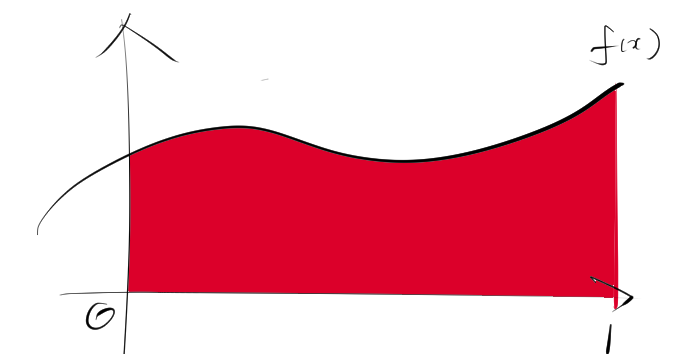次のように、$\dfrac{1}{n}$ずつに長方形に分割します。
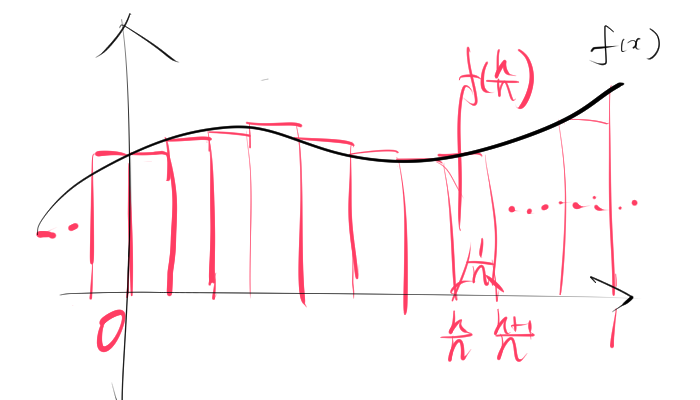長方形の面積は$\dfrac{1}{n}f \left(\dfrac{k}{n}\right)$です。$k$を$0$から$n-1$まで次のように足し合わせると、求めたい定積分の面積の近似になります。
$$\int_0^1 f(x) \, dx \approx\sum_{k=0}^{n-1}\frac{1}{n}f \left(\frac{k}{n}\right)$$
$n\to \infty$とすると、$\frac{1}{n}$ずつに分割しているため、分割した幅が0になるため、次のように定積分に等しくなる。
$$\int_0^1 f(x) \, dx = \lim_{n\to \infty}\sum_{k=0}^{n-1}\frac{1}{n}f \left(\frac{k}{n}\right)$$
1.2. aからbの範囲
aからbの範囲で次のような数式で表すことができます。
$$\int_a^b f(x) \, dx = \lim_{n\to \infty}\sum_{k=an}^{bn}\frac{1}{n}f \left(\frac{k}{n}\right)$$
基本的にシグマと定積分の範囲の関係はnで割ることで計算することができます。
例えば、$k=an+333$がスタートだとしたら、$n$で割って$a+\dfrac{333}{n}$となります。このとき、$n\to \infty$とすると$k$は$a$に収束するため、積分範囲は$a$から始まります。シグマの終わりの部分も同様に考えることができます。
2. 区分求積法の計算問題
2.1. 例題1：基本的な計算
\[ \lim_{n \to \infty} \left( \frac{1}{n+1} + \frac{1}{n+2} + \dots + \frac{1}{n+n} \right) \]
式全体は以下の形に書き直せます。
\[ \lim_{n \to \infty} \sum_{k=1}^{n} \frac{1}{n+k} \]
分子分母を \( \dfrac{1}{n+k} \) を \( n \) で割ると次のようになります。
\[ \lim_{n \to \infty}\sum_{k=1}^{n} \frac{1}{n}\cdot\frac{1}{ \left( 1 + \frac{k}{n} \right)} \]
シグマのスタートは1であることから$\dfrac{1}{n}$より、積分は0から始まります。
また、シグマの終わりはnであることから、$\dfrac{n}{n}$より、積分は1で終わります。
区間 \( [0, 1] \) 上の関数 \( \frac{1}{x+1} \) の積分に対応します。
\[ \lim_{n \to \infty}\sum_{k=1}^{n} \frac{1}{n}\cdot\frac{1}{ \left( 1 + \frac{k}{n} \right)} \]
\[= \int_0^1 \frac{1}{x+1} \, dx \]
$$=\log 2$$
2.2. 例題2：積分範囲が0~1以外
$$\lim_{n \to \infty} \left( \frac{n}{n^2+(2n)^2} + \frac{n}{n^2+(2n+1)^2} + \dots + \frac{n}{n^2+(5n)^2} \right) $$
式全体は以下の形に書き直せます。
\[ \lim_{n \to \infty} \sum_{k=2n}^{5n} \frac{n}{n^2+k^2} \]
分子分母を \( \dfrac{1}{n+k} \) を \( n^2 \) で割ると次のようになります。
\[ \lim_{n \to \infty}\sum_{k=2n}^{5n} \frac{1}{n}\cdot\frac{1}{ 1 + \left(\frac{k}{n}\right)^2 } \]
シグマのスタートは$2n$であることから$\dfrac{2n}{n}$より、積分は2から始まります。
また、シグマの終わりは$5n$であることから、$\dfrac{5n}{n}$より、積分は5で終わります。
区間 \( [2, 5] \) 上の関数 \( \dfrac{1}{1+x^2} \) の積分に対応します。
\[ \lim_{n \to \infty}\sum_{k=2n}^{5n}\frac{1}{n}\cdot\frac{1}{ 1 + \left(\frac{k}{n}\right)^2 } \]
\[= \int_2^5 \frac{1}{1+x^2} \, dx \]
$$=\left[ \tan^{-1}(x) \right]_2^5$$
$$ =\tan^{-1}(5) – \tan^{-1}(2)$$
2.3. 例題3：積の形
$$\lim_{n\to \infty}\left(\prod_{k=1}^{n} \frac{n}{k}\right)^{\frac{1}{n}}$$
$P_n$を次のように定義する。
\[ P_n = \prod_{k=1}^{n} \frac{n}{k} = \frac{n}{1} \cdot \frac{n}{2} \cdots \frac{n}{n} \]
$\displaystyle\lim_{n\to \infty} P_{n}^{\frac{1}{n}}$の極限を計算する。
$P_{n}^{\frac{1}{n}}$の対数をとり計算します。
$$\frac{1}{n}\log P_n$$
$$=\frac{1}{n}\left( \log \frac{n}{1}+\log \frac{n}{2} + \cdots \log \frac{n}{n} \right)$$
$$=\frac{1}{n}\sum^{n}_{k=1}\log \frac{n}{k}$$
$n\to \infty$の極限を計算すると次のようになる。
$$\lim_{n\to \infty}\frac{1}{n}\sum^{n}_{k=1}\log \frac{1}{\frac{k}{n}}$$
$$=\int_{0}^1 \log \frac{1}{x} \,dx$$
$$=-\int_{0}^1 \log x \,dx$$
$$=\left[-(x\log x-x)\right]^1_{0} = 1$$
対数をとっているので、実際の極限は次のようになります。
$$\lim_{n\to \infty}\left(\prod_{k=1}^{n} \frac{n}{k}\right)^{\frac{1}{n}} = e$$
