部分積分の導出・計算問題について

1. 部分積分とは
1.1. 部分積分の公式
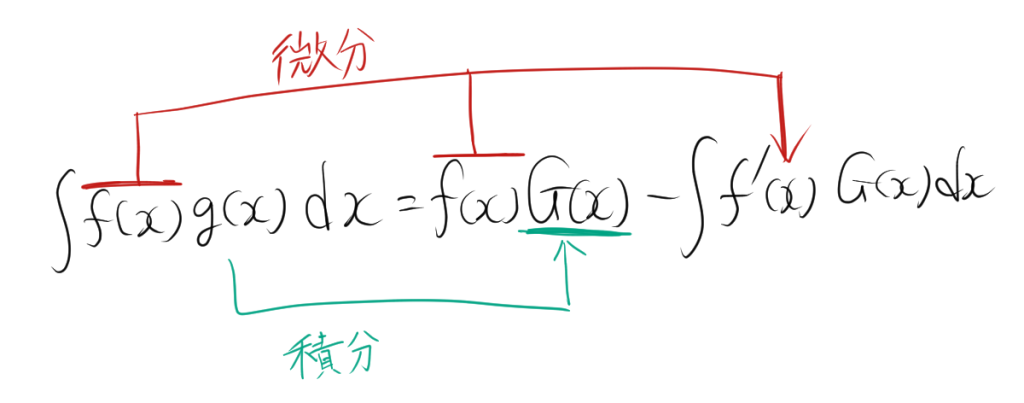
$$\int f(x) g(x) \, dx= f(x) G(x) -\int f'(x)G(x) \, dx$$
1.2. 部分積分の公式の導出
積の微分法則は次のように表されます。
\[ \frac{d}{dx} \left( f(x) g(x) \right) = f'(x) g(x) + f(x) g'(x) \]
この等式を積分してみましょう。
\[ \int \frac{d}{dx} \left( f(x) g(x) \right) \, dx = \int \left( f'(x) g(x) + f(x) g'(x) \right) \, dx \]
この式の左辺は、積分と微分が打ち消し合うため、次のように簡略化されます。
\[ f(x) g(x) = \int f'(x) g(x) \, dx + \int f(x) g'(x) \, dx \]
この式を整理すると、部分積分の公式が得られます。
\[ \int f(x) g'(x) \, dx = f(x) g(x) – \int f'(x) g(x) \, dx \]
この公式を使うと、元の積分を別の形に変えることができます。ここで、積分の対象を \( f(x) \) と \( g'(x) \) として選びますが、これらの選び方は積分を解く上で非常に重要です。具体的な例を使って部分積分を適用する方法を見てみましょう。
1.3. 部分積分のポイント
- 適切な \( f(x) \) と \( g(x) \) の選択が重要です。例えば、$f(x)$が$x$のとき、微分すると1になるので都合がいい。
- 部分積分を繰り返し適用する必要がある場合があります。
- 結果に積分定数 \( C \) を忘れずに加えます。
2. 部分積分の例題
2.1. 例題1:指数関数を含む部分積分
\[ \int x e^x \, dx \]
ここで、 \( f(x) = x \) および \( g'(x) = e^x \) と選びます。すると、 \( f'(x) = 1 \) および \( g(x) = \int e^x \, dx = e^x \) です。これを部分積分の公式に代入します。
\[ \int x e^x \, dx = x e^x – \int 1 \cdot e^x \, dx \]
\[ = x e^x – e^x + C \]
したがって、最終的な結果は次の通りです。
\[ \int x e^x \, dx = e^x (x – 1) + C \]
この手法を使うことで、積の形を持つ積分を解くことができるようになります。
2.2. 例題2:三角関数を含む積分
\[ \int x^2 \sin x\, dx \]
部分積分を適用すると、
\[ \int x^2 \sin x \, dx = -x^2 \cos x – \int -2x \cos x \, dx \]
\[ = -x^2 \cos x + 2 \int x \cos x \, dx \]
次に、\( \int x \cos x \, dx \) に対してもう一度部分積分を行います。
\[ \int x \cos x \, dx = x \sin x – \int \sin x \, dx \]
\[ = x \sin x + \cos x \]
したがって、
\[ \int x^2 \sin x \, dx = -x^2 \cos x + 2 \left( x \sin x + \cos x \right) \]
結果をまとめると、
\[ \int x^2 \sin x \, dx = -x^2 \cos x + 2x \sin x + 2\cos x + C \]
ここで、\( C \) は積分定数です。