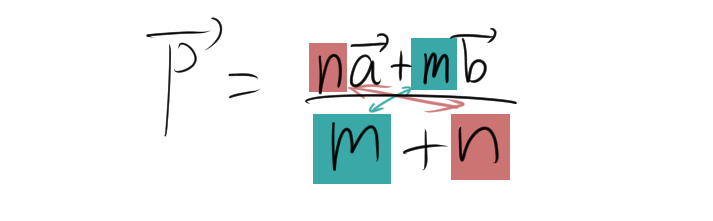内分点の位置ベクトルとは？導出と例題について

ふゅか

内分点の位置ベクトルって、線分をどれくらいの比率で分けるかをベクトルで表したのよね！

はるか

位置ベクトルの式を使うだけ。比率に応じて計算する

1. 内分点の位置ベクトルとは

この式は、点 \( P \) が点 \( A \) と点 \( B \) の位置を比 \( m:n \) で内分している場合の位置ベクトルを表しています。

1.1. 内分点の位置ベクトルの対応関係

1.2. 内分点の位置ベクトルの導出

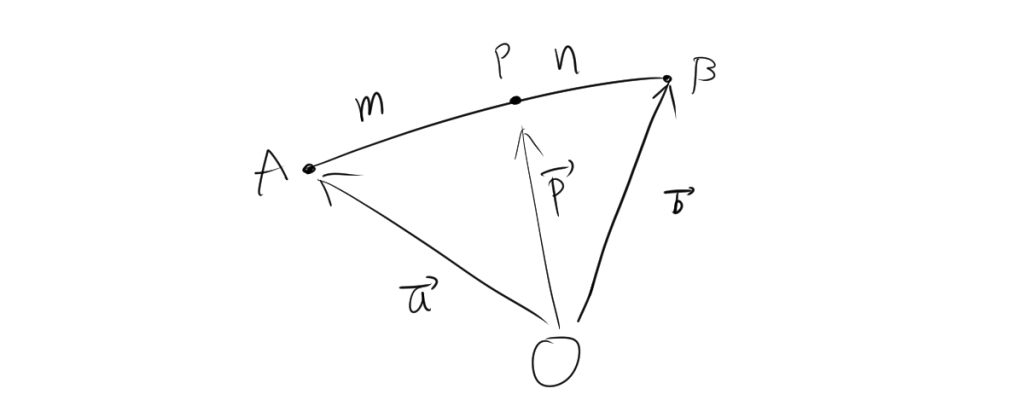
まず、点 $P$ が線分 $AB$ を内分する点であると考えます。点 \( A \)、\( B \)、および \( P \) への位置ベクトルを \(\overrightarrow{a}\)、\(\overrightarrow{b}\)、\(\overrightarrow{p}\) とします。ベクトル $\overrightarrow{OP}$ は、$\overrightarrow {OP} = \overrightarrow{OA}+\overrightarrow{AP}$より、

\[ \overrightarrow{p} = \overrightarrow{a} +\overrightarrow{AP}\]

ここで、$\overrightarrow{AP}=\frac{m}{m+n}\overrightarrow{AB}$となるので、

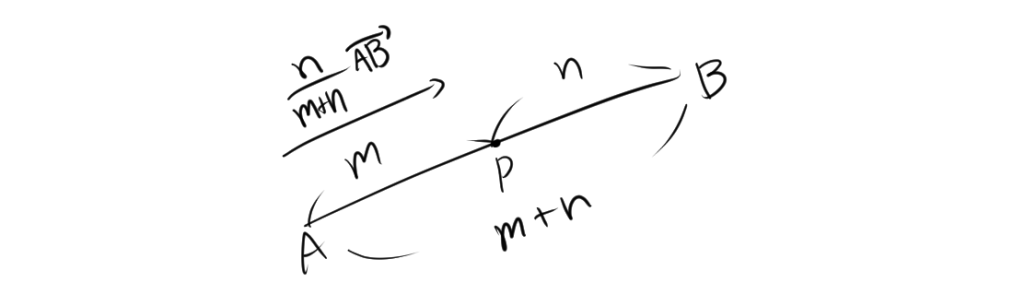\[ \overrightarrow{p} = \overrightarrow{a} +\frac{m}{m+n}\overrightarrow{AB}\]

次に、ベクトル $\overrightarrow{AB}$ は、$\overrightarrow{AB} = \overrightarrow{b}-\overrightarrow{a}$より、

$$\begin{align*} \overrightarrow{p} &= \overrightarrow{a} + \frac{m}{m+n}(\overrightarrow{b}-\overrightarrow{a}) \\ &= \frac{m+n}{m+n}\overrightarrow{a} + \frac{m}{m+n}(\overrightarrow{b}-\overrightarrow{a}) \\ &= \frac{n\overrightarrow{a} + m\overrightarrow{b}}{m+n} \end{align*}$$

ふゅか

PはABを内分する点だから、位置ベクトルの関係を使って考えるの。例えば、ベクトル \(\overrightarrow{AP}\) は \(\frac{m}{m+n} \overrightarrow{AB}\) になるんだよ。それを使って、最終的にAとBの位置ベクトルを利用して、Pの位置ベクトルが導けるの。

はるか

ふむ、\(\overrightarrow{AB}\) が \(\overrightarrow{b} – \overrightarrow{a}\) になることも利用するのか。

1.3. 具体例

例えば、点 \( A(2, 3) \) と点 \( B(8, 7) \) の間にある点 \( P \) が、線分 \( AB \) を \( 2:3 \) の比で内分する場合を考えます。点 \( A \) の位置ベクトルを \(\overrightarrow{a} = (2, 3)\)、点 \( B \) の位置ベクトルを \(\overrightarrow{b} = (8, 7)\) とします。

点 \( P \) の位置ベクトル \(\overrightarrow{p}\) は次のように求められます。

\[ \overrightarrow{p} = \frac{3 \cdot \overrightarrow{a} + 2 \cdot \overrightarrow{b}}{2 + 3} = \frac{3 (2, 3) + 2 (8, 7)}{5} \]

これを計算すると、

\[ \overrightarrow{p} = \frac{(6 + 16, 9 + 14)}{5} = \left( \frac{22}{5}, \frac{23}{5} \right) \]

つまり、点 \( P \) の位置ベクトルは \(\overrightarrow{p} = \left( \frac{22}{5}, \frac{23}{5} \right)\) となります。

2. 例題

2.1. 例題1

内分点の位置ベクトルは、以下の公式を使って求めることができます。

\[ \vec{p} = \frac{n\vec{a} + m\vec{b}}{m+n} \]

点 \( A(1, 2) \) と点 \( B(5, 6) \) を \( 3:2 \) の比で内分するので、点 \( P \) の位置ベクトルは次のように計算できます。

\[ \vec{p} = \frac{2 \cdot \vec{a} + 3 \cdot \vec{b}}{2 + 3} \]

\[ \vec{p} = \frac{2 \cdot (1, 2) + 3 \cdot (5, 6)}{5} \]

それぞれの成分ごとに計算すると、

\[ \vec{p} = \frac{(2 \times 1 + 3 \times 5, 2 \times 2 + 3 \times 6)}{5} \]

\[ \vec{p} = \frac{(2 + 15, 4 + 18)}{5} \]

\[ \vec{p} = \frac{(17, 22)}{5} \]

したがって、

\[ \vec{p} = \left( \frac{17}{5}, \frac{22}{5} \right) \]

これが点 \( P \) の位置ベクトルです。

2.2. 例題2

求めたいのは点 \( B \) の位置ベクトル \( \vec{b} \) です。公式に値を代入して、以下の式を立てます。

\[ (4, 3) = \frac{2 \cdot (2, 1) + 1 \cdot \vec{b}}{2 + 1} \]

\[ (4, 3) = \frac{(4, 2) + \vec{b}}{3} \]

両辺に 3 をかけて、次のようにします。

\[ (12, 9) = (4, 2) + \vec{b} \]

したがって、\( \vec{b} \) を求めるために、両辺から \( (4, 2) \) を引きます。

\[ \vec{b} = (12, 9) – (4, 2) \]

\[ \vec{b} = (8, 7) \]

したがって、点 \( B \) の位置ベクトルは

\[ \vec{b} = (8, 7) \]