更新:2024/12/13

イェンセン（Jensen）の不等式の意味と証明について

$はるか$

はるか

イェンセンの不等式か…凸関数と重み付き平均がポイント。

$ふゅか$

ふゅか

結構、いろいろな分野ででてくるよね！

1. イェンセンの不等式（凸不等式）
1.1. 数式の意味するところ
2. 凸関数と性質
2.1. 不等式
2.2. 図形的な性質
3. 数学的帰納法を利用した証明
4. 確率変数を利用した表現

1. イェンセンの不等式（凸不等式）

凸関数 $ f(x) $ に対して、任意の実数 $ x_1, x_2, \ldots, x_n $ と非負の重み $ \lambda_1, \lambda_2, \ldots, \lambda_n $ が以下を満たすとします。

\[ \lambda_i \geq 0, \quad \sum_{i=1}^n \lambda_i = 1 \]

このとき、次の不等式が成り立ちます

\[ f\left( \sum_{i=1}^n \lambda_i x_i \right) \leq \sum_{i=1}^n \lambda_i f(x_i) \]

$はるか$

はるか

要するに、凸関数fに対して、f(重み付き平均) ≤ 重み付き平均(f) 。

1.1. 数式の意味するところ

左辺は、加重平均に凸関数 $ f $ を適用した結果です。
右辺は、各点に凸関数 $ f $ を適用した結果の加重平均です。
凸関数では、入力値の加重平均を関数に適用した値（左辺）は、関数を各入力値に適用して加重平均した値（右辺）よりも小さくなる。

2. 凸関数と性質

イェンセンの不等式における関数fは凸関数です。この凸関数には次のような性質があります。

2.1. 不等式

関数 $ f(x) $ が凸であるとは、任意の $ x, y \in \mathbb{R} $ と $ \lambda \in [0, 1] $ に対して以下の不等式を満たす。

\[ f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda)f(y) \]

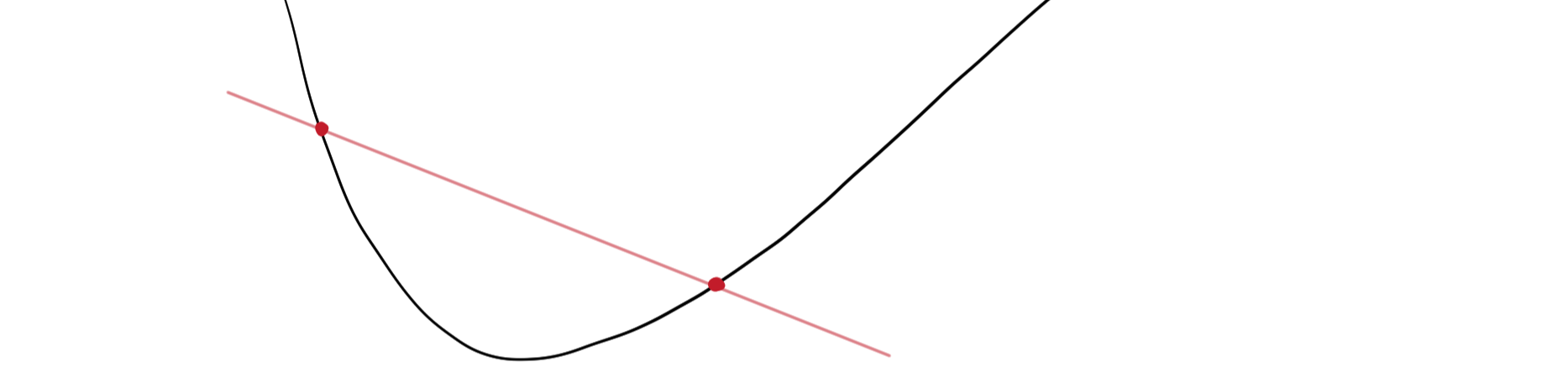
2.2. 図形的な性質

任意の点、$(x,f(x))$、$(x_2,f(x_2))$を結んだときに、関数fよりも、直線が上側にある。

$はるか$

はるか

凸関数は線で結ぶと曲線が下にある状態…と。

3. 数学的帰納法を利用した証明

数学的帰納法を用いて証明します。ここで、

\[ f\left( \sum_{i=1}^n \lambda_i x_i \right) – \sum_{i=1}^n \lambda_i f(x_i) \leq 0 \]

として証明を行います。

まず、$ n = 2 $ のとき、凸関数の性質から次の不等式が成り立ちます。

\[ f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda)f(y), \quad \lambda \in [0, 1] \]

したがって、

\[ f(\lambda x + (1-\lambda)y) \lambda f(x) + (1-\lambda)f(y)\leq 0, \quad \lambda \in [0, 1] \]

これから、任意の $ \lambda_1, \lambda_2 \geq 0 $ かつ $ \lambda_1 + \lambda_2 = 1 $ のとき、

\[ f(\lambda_1 x_1 + \lambda_2 x_2)- \lambda_1 f(x_1) + \lambda_2 f(x_2) \leq 0 \]

したがって、$ n = 2 $ の場合、イェンセンの不等式は成り立ちます。

$ n = k $ の場合、$\lambda_1, \lambda_2, \ldots, \lambda_{k} \geq 0$ かつ $\displaystyle\sum_{i=1}^{k} \lambda_i = 1$ としたとき、次が成り立つと仮定します。

\[ f\left( \sum_{i=1}^k \lambda_i x_i \right) – \sum_{i=1}^k \lambda_i f(x_i) \leq 0\]

次に、$ n = k+1 $ のとき、$\lambda_1, \lambda_2, \ldots, \lambda_{k+1} \geq 0$ かつ $\displaystyle\sum_{i=1}^{k+1} \lambda_i = 1$ とします。

ここで、

\[ \lambda = \sum_{i=1}^k \lambda_i \]

とおくと、$\lambda_{k+1} = 1 – \lambda$ となります。

もし $\lambda = 0$ であれば、$\lambda_{k+1} = 1$ であり、この場合、

\[ f(\lambda_1 x_1 + \cdots + \lambda_k x_k + \lambda_{k+1} x_{k+1}) = f(x_{k+1}) \] かつ

\[ \sum_{i=1}^{k+1} \lambda_i f(x_i) = f(x_{k+1}) \] となるので不等式は成り立ちます。

よって以降は $\lambda > 0$ とします。$\lambda > 0$ のとき、$\frac{\lambda_i}{\lambda}$ ($ i=1, \ldots, k $) は非負で総和が1になるので、帰納法の仮定を用いることができます。すなわち、

\[f\left(\sum_{i=1}^k \frac{\lambda_i}{\lambda} x_i \right) – \sum_{i=1}^k \frac{\lambda_i}{\lambda} f(x_i) \leq 0 \]

これに $\lambda$ を掛けると、

\[ \begin{align*} &\lambda f\left(\sum_{i=1}^k \frac{\lambda_i}{\lambda} x_i \right) – \sum_{i=1}^k \lambda_i f(x_i) \leq 0 \\ &\lambda f\left(\sum_{i=1}^k \frac{\lambda_i}{\lambda} x_i \right) \leq \sum_{i=1}^k \lambda_i f(x_i) \end{align*}\]

一方で、$f\left(\sum_{i=1}^{k+1} \lambda_i x_i\right)$の数式に戻ると、

\[ f\left(\sum_{i=1}^{k+1} \lambda_i x_i\right) = f\left(\lambda \cdot \frac{\sum_{i=1}^k \lambda_i x_i}{\lambda} + (1-\lambda) x_{k+1}\right) \]

ここで、凸関数の性質（n=2の場合と同じ）より、$\lambda \in [0,1]$ かつ $1-\lambda \in [0,1]$ なので、

\[ \begin{align*} &f\left(\sum_{i=1}^{k+1} \lambda_i x_i\right)-\sum_{i=1}^{k+1} \lambda_i f(x_i) \\ &=f\left(\lambda \cdot \frac{\sum_{i=1}^k \lambda_i x_i}{\lambda} + (1-\lambda)x_{k+1}\right)-\sum_{i=1}^{k+1} \lambda_i f(x_i) \\ &\leq \lambda f\left(\frac{\sum_{i=1}^k \lambda_i x_i}{\lambda}\right) + (1-\lambda)f(x_{k+1})-\sum_{i=1}^{k+1} \lambda_i f(x_i) \\ & \leq \sum_{i=1}^k \lambda_i f(x_i) + (1-\lambda)f(x_{k+1})-\sum_{i=1}^{k+1} \lambda_i f(x_i) \\ &= \sum_{i=1}^{k+1} \lambda_i f(x_i)-\sum_{i=1}^{k+1} \lambda_i f(x_i) \\ &=0 \end{align*} \]

よって、 \[ f\left(\sum_{i=1}^{k+1} \lambda_i x_i\right) – \sum_{i=1}^{k+1} \lambda_i f(x_i) \leq 0 \] が示されました。

$ n=2 $ の場合に成立し、$ n=k $ で成立すると仮定すると $ n=k+1 $ でも成立することを示しました。よって、数学的帰納法により、任意の自然数 $ n $ について、 \[ f\left(\sum_{i=1}^n \lambda_i x_i \right) – \sum_{i=1}^n \lambda_i f(x_i) \leq 0 \] が成り立ちます。