ジョルダンの不等式の証明・グラフ・微分について

1. ジョルダンの不等式とは
\[ \frac{2}{\pi} \theta \leq \sin \theta \leq \theta \quad \left(0 \leq θ \leq \frac{\pi}{2}\right) \]
この不等式は、\( \theta \) が \( 0 \) から \( \pi/2 \) の範囲で正の値を取るとき、三角関数の \( \sin \theta \)は一次関数で挟むことができることを示しています。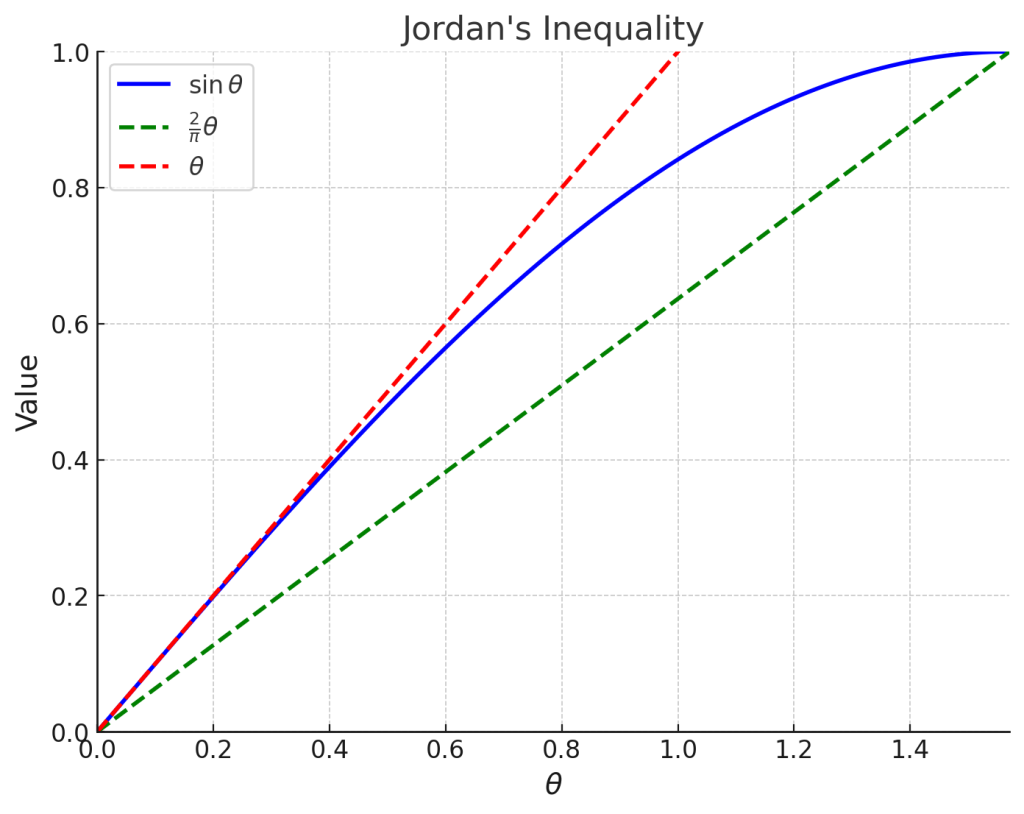
1.1. 微分を利用した証明
不等式の両端を分けて考える
[1]\(\sin \theta \leq \theta\) の証明を行います。
この不等式を証明するために、関数 \( f(\theta) = \theta – \sin \theta \) を考えます。この関数が \( 0 \leq \theta \leq \frac{\pi}{2} \) の範囲で常に正またはゼロであれば、不等式が成り立つことが分かります。
\( f(\theta) = \theta – \sin \theta \) の微分をすると次のようになります。
\[ f'(\theta) = 1 – \cos \theta \]
\( 1 – \cos \theta \) は \( 0 \leq \theta \leq \frac{\pi}{2} \) で常に正またはゼロです。つまり、\( f(\theta) \) はこの範囲で単調増加します。\( \theta = 0 \) のとき、\( f(0) = 0 \) です。
したがって、\( 0 \leq \theta \leq \frac{\pi}{2} \) の範囲では \( f(\theta) = \theta – \sin \theta \geq 0 \) が成立するため、\( \sin \theta \leq \theta \) が成り立ちます。
次に、\(\frac{2}{\pi} \theta \leq \sin \theta\) の証明を行います。
この不等式を証明するために、今度は関数 \( g(\theta) = \sin \theta – \frac{2}{\pi} \theta \) を考えます。この関数が \( 0 \leq \theta \leq \frac{\pi}{2} \) の範囲で常にゼロ以上であれば、不等式が成り立ちます。
\( g(\theta) = \sin \theta – \frac{2}{\pi} \theta \) の微分をすると、次のようになります。
\[ g'(\theta) = \cos \theta – \frac{2}{\pi} \]
\( \cos \theta \) は \( 0 \leq \theta \leq \frac{\pi}{2} \) で \( 1 \) から \( 0 \) の間の値を取り、\( \frac{2}{\pi} \approx 0.6366 \) です。
したがって、$g(\theta)$は \( 1 \) から \( 0 \) の間で途中まで増加して、減少することがわかる。よって,
$g(0)$または$g(\frac{\pi}{2})$のどちらかが最小値になる。
次に、\( \theta = 0 \) のとき、\( g(0) = 0 \) です。また、\( \theta = \frac{\pi}{2} \) のとき、\( g\left(\frac{\pi}{2}\right) = 1 – \frac{2}{\pi} \cdot \frac{\pi}{2} = 0 \) です。
したがって、\( 0 \leq \theta \leq \frac{\pi}{2} \) の範囲では \( g(\theta) \geq 0 \) であるため、\( \frac{2}{\pi} \theta \leq \sin \theta \) が成り立ちます。
以上の2つの不等式を組み合わせることで、ジョルダンの不等式
\[ \frac{2}{\pi} \theta \leq \sin \theta \leq \theta \quad (0 \leq \theta \leq \frac{\pi}{2}) \]
が成り立つことを証明できました。



