三角関数の加法定理の4つの証明について

ふゅか

加法定理って、最初は6つの式があってちょっと混乱するよね。でも、実は1つの式を理解すれば、他のも全部芋づる式に解けるんだよ！

はるか

うん、たった一つの式から導ける。まずは、$\cos(\alpha – \beta)$ から証明する。

1. 加法定理

加法定理といえば6つの式があり、証明が面倒だなというイメージを持っているかもしれません。ですが、たった一つの式を証明すれば芋づる形式でほかの加法定理を導くことができます。

2. 加法定理の証明

2.1. アプローチ

$$\cos \left( \alpha -\beta -\dfrac{\pi }{2}\right) =\sin \left( \alpha -\beta \right) $$

$$\tan \left( \alpha -\beta \right) =\dfrac{\sin \left( \alpha -\beta \right) }{\cos \left( \alpha -\beta \right) }$$

$-\beta$を$\beta$することで、$\cos \left( \alpha -\beta \right)$が証明できれば、ほかの加法定理を証明することができる。

ふゅか

じゃあ、$\cos (\alpha – \beta)$の証明方法を見てみよう！単位円と余弦定理を使うんだよね？

はるか

そう。ベクトル内積でもできるけど、まずは余弦定理から。

2.2. $\cos \left( \alpha -\beta \right)$の証明1：単位円と余弦定理

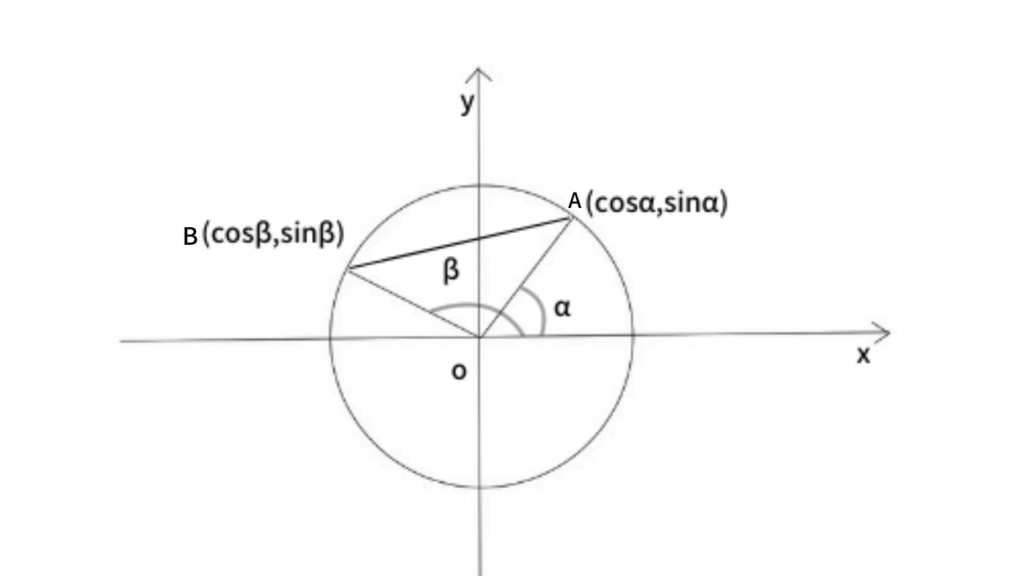
単位円と余弦定理を使う。余弦定理より、
$$AB^{2}=OA^{2}+OB^{2}-2OA\cdot OB\cos \left( \alpha -\beta \right) $$

$$\left( \cos \alpha -\cos \beta \right) ^{2}+\left( \sin \alpha -\sin \beta \right) ^{2}=1^{2}+1^{2}-2\cos \left( \alpha -\beta \right) $$

$$\Leftrightarrow 2-2\sin \alpha \sin \beta -2\cos \alpha \cos \beta =2-2\cos\left( \alpha -\beta \right) $$

$$\therefore\cos \left( \alpha -\beta \right) =\cos \alpha \cos \beta +\sin \alpha \sin \beta $$

2.3. $\cos \left( \alpha -\beta \right)$の証明2：単位円と内積

単位円とベクトルの内積を使う。ベクトルの内積より、

$$\overrightarrow{OA}\cdot \overrightarrow{OB}=\left| \overrightarrow{OA}\right| \left| \overrightarrow{OB}\right| \cos \left( \alpha -\beta \right)$$

$\overrightarrow{OA}=\begin{pmatrix} \cos \alpha \\ \sin \alpha \end{pmatrix}$, $\overrightarrow{OB}=\begin{pmatrix} \cos \beta \\ \sin \beta \end{pmatrix}$であるので、

$$\begin{pmatrix} \cos \alpha \\ \sin \alpha \end{pmatrix}\cdot \begin{pmatrix} \cos \beta \\ \sin \beta \end{pmatrix}=\left| \cos ^{2}\alpha +\sin ^{2}\alpha\right| \cdot \left| \cos ^{2}\beta +\sin ^{2}\beta \right| \cos \left( \alpha -\beta \right) $$

$$\therefore\cos \left( \alpha -\beta \right) =\cos \alpha \cos \beta +\sin \alpha \sin \beta $$

2.4. $\cos \left( \alpha -\beta \right)$の証明3：回転行列

単位円上の点C$(\cos(-\beta),\sin(-\beta))$を$\alpha$だけ行列の回転移動で考えると、

$$\begin{bmatrix} \cos \left( \alpha -\beta \right) \\ \sin \left( \alpha -\beta \right) \end{bmatrix}$$

$$=\begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix}\begin{bmatrix} \cos \left( -\beta \right) \\ \sin \left( -\beta \right) \end{bmatrix}$$

$$=\begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix}\begin{bmatrix} \cos \left(\beta \right) \\ -\sin \left( \beta \right) \end{bmatrix}$$

$$=\begin{bmatrix} \cos \alpha \cos \beta +\sin \alpha \sin \beta \\ \sin \alpha \cos \beta -\cos \alpha \sin \beta \end{bmatrix}$$

2.5. $\cos \left( \alpha -\beta \right)$の証明４：複素数平面と単位円

複素数平面の単位円上の点A($z=\cos \alpha +i\sin \alpha $)を$-\beta$だけ回転移動したと考える。

$\cos \left( -\beta \right) +i\sin \left( -\beta \right) $をzにかけれた複素数をwとすると、

$$w=\left( \cos \alpha +i\sin \alpha \right) \left( \cos \beta -i\sin \beta \right) $$

$$=\cos \alpha \cos \beta +\sin \alpha \sin \beta +i\left( \sin \alpha \cos \beta -\cos \alpha \sin \beta \right) $$

また、$w=\cos \left( \alpha -\beta \right) +i\sin \left( \alpha -\beta \right) $より、

$$\sin \left( \alpha -\beta \right) =\sin \alpha \cos \beta -\cos \alpha \sin \beta $$

$$\cos \left( \alpha -\beta \right) =\cos \alpha \cos \beta +\sin \alpha \sin \beta $$

2.6. 残りの加法定理を導く

$\sin \left( \alpha -\beta \right)$を計算すると次のようになる。

$$\sin \left( \alpha -\beta \right)$$

$$=\cos\left( \alpha -\beta -\dfrac{\pi }{2}\right) $$

$$=\cos \left\{ \left( \alpha -\dfrac{\pi }{2}\right) -\beta \right\} $$

$$=\cos \left( \alpha -\dfrac{\pi }{2}\right) \cos \beta +\sin \left( \alpha -\dfrac{\pi }{2}\right) \sin \beta $$

$$=\sin \alpha \cos \beta +\cos \alpha \sin \beta $$

$\tan \left( \alpha -\beta \right) $を計算すると次のようになる。

$$\tan \left( \alpha -\beta \right) $$

$$=\dfrac{\sin \left( \alpha -\beta \right) }{\cos \left( \alpha -\beta \right) }$$

$$=\dfrac{\sin \alpha \cos \beta -\cos \alpha \sin \beta}{\cos \alpha \cos \beta +\sin \alpha \sin \beta}$$

$\cos \alpha \cos \beta\neq 0$で割ると、

$$=\dfrac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }$$

そして$-\beta$を$\beta$とすれば、加法定理の和のほうが求めることができる。