karamataの不等式の意味と証明について

1. Karamataの不等式
凸関数 \( f \) が与えられたとき、非負かつ増加しない数列 \( \mathbf{x} = (x_1, x_2, \ldots, x_n) \) と \( \mathbf{y} = (y_1, y_2, \ldots, y_n) \) について、$[\mathbf x] \succeq [\mathbf y]$であるとき、次の不等式が成り立ちます。
\[ \sum_{i=1}^n f(x_i) \geq \sum_{i=1}^n f(y_i) \]
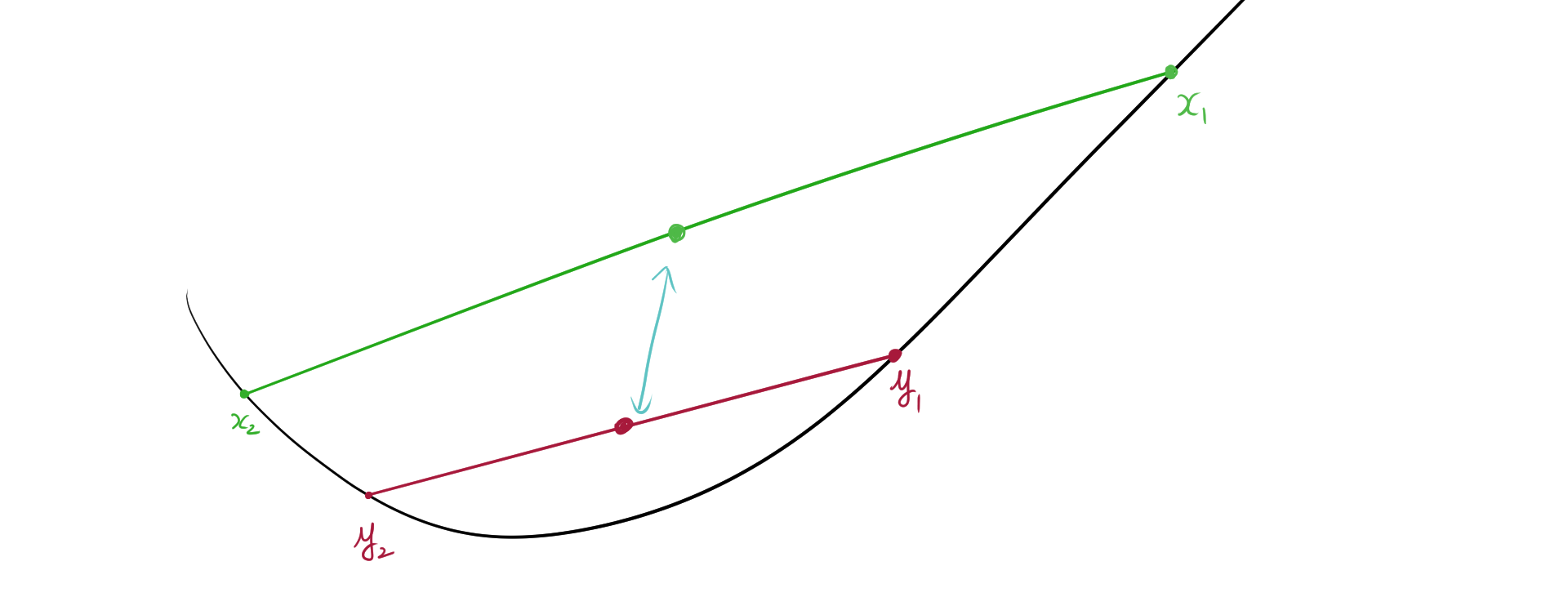
1.1. イメージ
n=2のときは、図形的には直線の中点を意味しており、次のような関係が成り立ちます。
2. majorize
この不等式を理解するうえで、$\mathbf x \succeq \mathbf y$について知る必要があります。記号「$\succeq $」は、Muirheadの不等式でも紹介しています。
この記号は「majorize」と呼ばれて、簡単に言うと、どちらの数列が偏っているのかを示しています。
majorizeは次の二つを満たしています。
$\mathbf{x} \succeq \mathbf{y}$ は、次の 2 つの条件が成り立つ場合に成立します。
部分和が各段階で $\mathbf{x}$ の方が大きいか等しい。
\[ \sum_{i=1}^k x_{i} \geq \sum_{i=1}^k y_{i} \quad (\forall k \in \{1, 2, \dots, n-1\}) \]
総和は等しい。
\[ \sum_{i=1}^n x_{(i)} = \sum_{i=1}^n y_{(i)} \]
2.1. 例
$[\mathbf{x}] \succeq [\mathbf{y}]$かどうか確認してみましょう。
- 数列 $\mathbf{x} = (5, 3, 2)$ と $\mathbf{y} = (4, 3, 3)$ を考えます。
- 総和は$\mathbf{x}$と$\mathbf{y}$ともに10となって、等しいです。
- 累積和を確認します
- $k = 1$ のとき、$5 \geq 4$。
- $k = 2$ のとき、$5+3 = 8 \geq 4+3 = 7$。
- $k = 3$ のとき、$5+3+2 = 10 = 4+3+3 = 10$。
よって、$\mathbf{x} \succeq \mathbf{y}$ が成り立ちます。
- もし $\mathbf{x} = (5, 3, 2)$ と $\mathbf{y} = (6, 3, 1)$ ならば
- $k = 2$ のとき $5+3 = 8 \not\geq 6+2 = 9$ なので、$\mathbf{x} \succeq \mathbf{y}$ は成り立ちません。
3. n=2,3の場合
3.1. n=2,3の場合
\( n = 2 \) の場合
ここで、凸関数 \( f \) を考えると、次が成り立ちます。
\[ f(x_1) + f(x_2) \geq f(y_1) + f(y_2) \]
3.2. 凸関数$x^2$の計算例
関数 \( f(x) = x^2 \) を用いて、\( x_1 = 2, x_2 = 3, x_3 = 4 \)、\( y_1 = 1, y_2 = 2, y_3 = 3 \) とします。
計算: \[ f(x_1) + f(x_2) + f(x_3) = f(2) + f(3) + f(4) = 4 + 9 + 16 = 29 \] \[ f(y_1) + f(y_2) + f(y_3) = f(1) + f(2) + f(3) = 1 + 4 + 9 = 14 \]
結果: \[ f(x_1) + f(x_2) + f(x_3) \geq f(y_1) + f(y_2) + f(y_3) \quad \text{(29 ≥ 14)} \]
4. 不等式の証明
\([\mathbf x]\succeq [\mathbf y]\) より、部分和を \[ X_k = \sum_{j=1}^k x_j,\quad Y_k = \sum_{j=1}^k y_j \] と定めると、\(1 \leq m < n\) について \[ X_m \ge Y_m,\quad \text{かつ}\quad X_n = Y_n \] が成立する。
凸関数 \(f\) の性質と$\mathbf x$と$\mathbf y$は非負かつ増加しない数列であることから、区間上での平均傾き$c_k$は単調減少の数列になる。
\[ c_k = \frac{f(y_k) – f(x_k)}{y_k – x_k} \quad (y_k \neq x_k \text{ の場合}) \]
もし \(x_k = y_k\) である場合には、その点での微分係数 \(f'(x_k)\) を \(c_k\) とする。
次に、アーベルの総和公式を用いると、$f(x_k) – f(y_k) = c_k (x_k – y_k)$となることから、
\[ \begin{align*}\sum_{k=1}^n (f(x_k) – f(y_k)) &= \sum_{k=1}^n c_k (x_k – y_k) \\ &=c_n(X_n – Y_n) + \sum_{k=1}^{n-1} (c_k – c_{k+1})(X_k – Y_k) \end{align*}\]
ここで、\([\mathbf x]\succeq [\mathbf y]\) により \(X_k – Y_k \geq 0\) と \(c_k\) は減少列であるから、\(c_k – c_{k+1} \geq 0\) となる。よって各項 \((c_k – c_{k+1})(X_k – Y_k) \ge 0\) が成立する。
\[ c_n(X_n – Y_n) + \sum_{k=1}^{n-1} (c_k – c_{k+1})(X_k – Y_k) \geq 0\]
したがって、
\[ \sum_{k=1}^n (f(x_k) – f(y_k)) \geq 0 \]
すなわち
\[ \sum_{k=1}^n f(x_k) \geq \sum_{k=1}^n f(y_k) \]
が得られる。