線形写像の核の定義・具体例・性質・例題について

1. 線形写像の核とは
1.1. 核の定義
\[ \text{ker}(f) = \{ v \in V \mid f(v) = 0 \} \]
ここで、
- \( V \) は線形空間(ベクトル空間)で、線形写像 \( f \) の定義域。
- \( W \) は線形空間(ベクトル空間)で、線形写像 \( f \) の値域。
- \( 0 \) は値域 \( W \) のゼロベクトル。
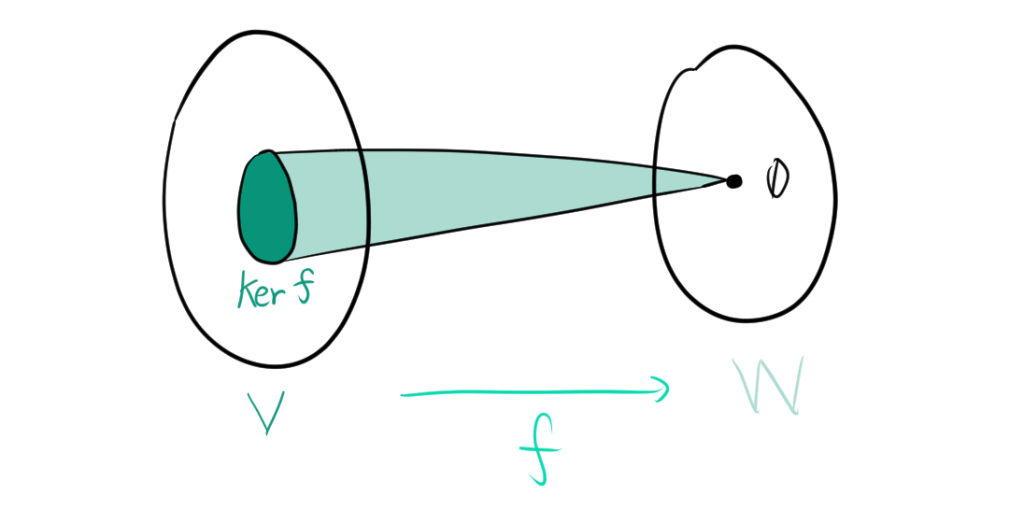
1.2. 核のイメージ
核のイメージは次のようになります。
2. 核の性質
2.1. 部分空間
$W$の0ベクトルを$0_W$とする。任意の \(u, v \in \text{ker}(f)\) を取ります。このとき、\( f(u) = 0_W \) および \( f(v) = 0_W \) です。ベクトルの加法に関して、
\[ f(u + v) = f(u) + f(v) = 0_W + 0_W = 0_W \]
したがって、\( u + v \in \text{ker}(f) \) です。これにより、\(\text{ker}(f)\) が加法に関して閉じていることが示されました。
任意の \(u \in \text{ker}(f)\) と任意のスカラー \(c \in \mathbb{R}\)(または \(\mathbb{C}\))を取ります。このとき、\( f(u) = 0_W \) です。スカラー乗算に関して、
\[ f(c u) = c f(u) = c \cdot 0_W = 0_W \]
したがって、\( c u \in \text{ker}(f) \) です。これにより、\(\text{ker}(f)\) がスカラー乗算に関して閉じていることが示されました。
以上の条件を満たすため、\(\text{ker}(f)\) は線形空間 \(V\) の部分空間であることが示されました。
2.2. 次元定理(ランク・ヌル定理)
\[ \dim(V) = \dim(\text{ker}(f)) + \dim(\text{Im}(f)) \]
という関係が成り立ちます。
3. 例題
3.1. 例題1:部分空間
\[ f(x, y, z) = (2x – y, x + 3y + z) \]
この線形写像 \( f \) の核($\text{Ker}(f)$)を求めてください。
\( \text{Ker}(f) \) は \( f(v) = 0 \) を満たすベクトル \( v = (x, y, z) \in \mathbb{R}^3 \) の集合です。
\( f(x, y, z) = 0 \) すなわち、次の連立方程式を解く必要があります。
\[ \begin{cases} 2x – y = 0 \\ x + 3y + z = 0 \end{cases} \]
$x=t$とする。
第1式から、\( y = 2t \)。
第2式に \( y = 2t \) を代入して、\( t+ 3(2t) + z = 0 \) となり、\( t + 6t + z = 0 \) つまり、\( 7t+ z = 0 \) です。
これを \( z = -7t \) と書けます。
よって、核のベクトル \( (x, y, z) \) は次のようになります。
$$\begin{bmatrix} x \\ y \\ z \end{bmatrix} = t\begin{bmatrix} 1 \\ 2 \\ -7 \end{bmatrix} $$
核は次のように表されます。
\[ \text{Ker}(f) = \{ (x, y, z) \in \mathbb{R}^3 \mid (x, y, z) = t(1, 2, -7), t \in \mathbb{R} \} \]
3.2. 例題2:部分空間
\[ T(x, y, z) = (x + y, y + z) \]
このとき、\( T(x, y, z) = 0 \) となるベクトル \( (x, y, z) \) を求めなさい。
\[ x + y = 0 \]
\[ y + z = 0 \]
$y=t$と置くと、これを解くと、
\[ x = -t, \quad z = -t \]
したがって、ベクトル\( (x, y, z) \) は次のようになります。
$$\begin{bmatrix} x \\ y \\ z \end{bmatrix} = t\begin{bmatrix} -1 \\ 1 \\ -1 \end{bmatrix} $$
この例では、核の次元は1です。