1/2mv^2とは何か?運動エネルギーの基礎

1. 運動エネルギーとは
\[ K = \frac{1}{2}mv^2 \]
- 質量(\( m \)):物体の質量は、その物体が持つ物質の量を示します。質量が大きいほど、同じ速度で運動する場合の運動エネルギーも大きくなります。
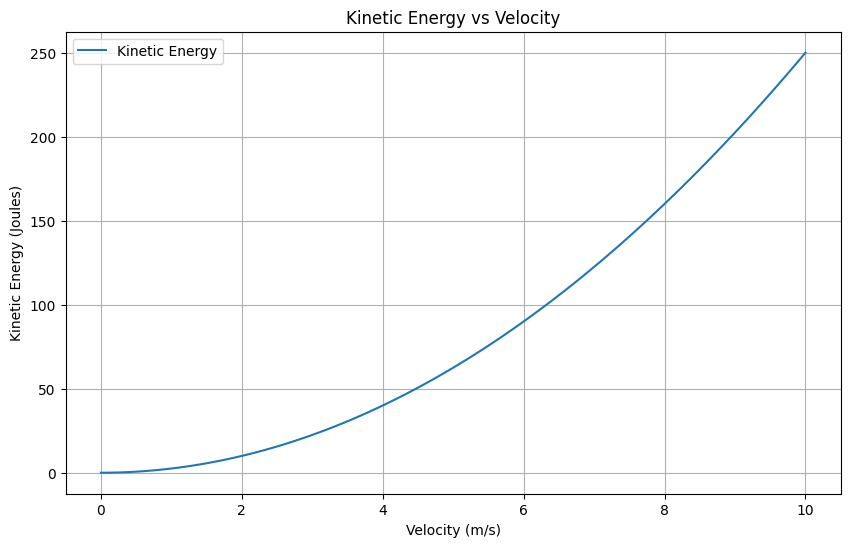
- 速度(\( v \)):物体の速度は、その物体が移動する速さを示します。速度が速いほど、運動エネルギーは大きくなります。特に、速度は二乗されるため、速度が増えると運動エネルギーは非常に大きく増加します。
1.1. 運動エネルギーの例
- 自動車:質量が1,500 kgの自動車が時速60 km(約16.67 m/s)で走っているときの運動エネルギーを計算してみましょう。 \[ K = \frac{1}{2} \times 1500 \, \text{kg} \times (16.67 \, \text{m/s})^2 \] \[ K \fallingdotseq 208416.675 \, \text{J} \]
- 野球のボール:質量が0.145 kgの野球のボールが秒速40 mで投げられるときの運動エネルギーを計算してみましょう。 \[ K = \frac{1}{2} \times 0.145 \, \text{kg} \times (40 \, \text{m/s})^2 \]\[ K = 116 \, \text{J} \]
2. 運動エネルギーの単位
運動エネルギーの単位は、質量の単位と速度の単位から導き出されます。
- 質量の単位: 質量の標準単位はキログラム (kg) です。
- 速度の単位: 速度の標準単位はメートル毎秒 (m/s) です。
運動エネルギーの単位は式 \(\frac{1}{2}mv^2\) に従って、次のように計算されます。
\[ [K] = \frac{1}{2} \times [m] \times [v]^2 \] \[ [K] = kg \times \left(\frac{m}{s}\right)^2 \] \[ [K] = kg \times \frac{m^2}{s^2} \]
\[ 1 \text{J} = 1 \text{kg} \cdot \frac{m^2}{s^2} \]
3. 運動エネルギーの導出
運動エネルギー\(K= \frac{1}{2}mv^2 \) の導出を説明します。
3.1. 仕事・エネルギーの原理
物体に対して行われる仕事 \( W \) は、その物体の運動エネルギーの変化として表されます。仕事は力 \( F \) とその力が働く距離 \( d \) の積で定義されます。
\[ W = F \cdot d \]
ニュートンの第二法則 \( F = ma \) より、
\[ W = F \cdot d = ma \cdot d \]
3.2. 速度と加速度の関係
速度 \( v \) と加速度 \( a \) は次の方程式で関係付けられます。
\[ v^2 = v_0^2 + 2ad \]
ここで、\( v_0 \) は初速度、\( v \) は最終速度、\( a \) は加速度、\( d \) は移動距離です。初速度 \( v_0 \) が 0 である場合、この方程式は以下のようになります。
\[ v^2 = 2ad \]
3.3. 仕事と運動エネルギー
先程の運動方程式 \( v^2 = 2ad \) を使って、加速度と移動距離の関係を変形します。
\[ ad = \frac{v^2}{2} \]
これを仕事の式に代入すると、
\[ W = m \cdot \frac{v^2}{2} \]
この仕事 \( W \) が物体の運動エネルギー \( K \) であるため、
\[ K = \frac{1}{2}mv^2 \]
このようにして、運動エネルギーの公式が導出されます。




