交代行列の性質や具体例について

1. 交代行列

つまり、対角成分を軸に対称的な要素$a_{ij}$と$a_{ji}$は$a_{ij}=-a_{ji}$を満たしているということです。

1.1. 交代行列の具体例

2次の交代行列

$\begin{bmatrix} 0 & -2 \\ 2 & 0 \end{bmatrix}$

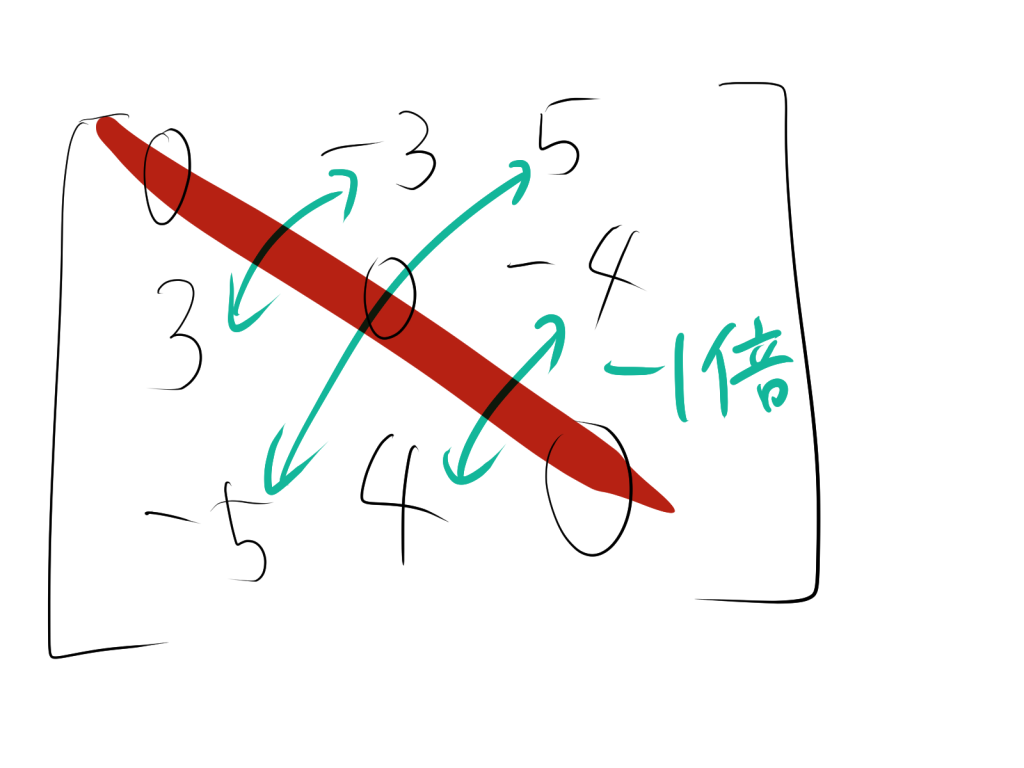
3次の交代行列

$\begin{bmatrix} 0 & -3 & 5 \\ 3 & 0 & -4 \\ -5 & 4 & 0 \\ \end{bmatrix}$

2. 交代行列の性質

2.1. 奇数次の行列式は0になる

$A$を$n$次の交代行列とする。

$\mathrm{det}A$

$=\mathrm{det}A^T$

$=\mathrm{det}(-A)$

$=(-1)^n\mathrm{det}A$

となる。$n$が奇数であるとき、自然数$k$を用いて$n=2k-1$と表すと

$=(-1)^{2k-1}\mathrm{det}A$

$=-\mathrm{det}A$

となる。$\mathrm{det}A=-\mathrm{det}A$より、

$2\mathrm{det}A=0$

$\therefore\mathrm{det}A=0$

---

行列Aの行列式を求める。

$=\begin{vmatrix} 0 & -a & c \\ a & 0 & -b \\ -c & b & 0 \\ \end{vmatrix}$

$=-abc+abc$

$=0$

2.2. 対角成分は0になる

$a_{ij}$と$a_{ji}$は$a_{ij}=-a_{ji}$を満たしているから、

$a_{ii}=-a_{ii}$

$\therefore a_{ii}=0$

と、対角成分は0になる。

2.3. $A^T-A$は交代行列になる

交代行列になるかどうか確認するためには転置をすればわかるから、

$(A^T-A)^T$

$=(A^T)^T-A^T$

$=A-A^T$

$=-(A^T-A)$

となるため、交代行列になる。

---

$A^T-A$は交代行列になるか確認してみましょう！

$A^T-A$を計算する。

$A^T-A$

$=\begin{bmatrix} 0 & a & -c \\ -a & 0 & b \\ c & -b & 0 \\ \end{bmatrix}-\begin{bmatrix} 0 & -a & c \\ a & 0 & -b \\ -c & b & 0 \\\end{bmatrix}$

$=\begin{bmatrix} 0 & 2a & -2c \\ -2a & 0 & 2b \\ 2c & -2b & 0 \\ \end{bmatrix}$

次に、$(A^T-A)^T$を求める。

$(A^T-A)^T$

$=\begin{bmatrix} 0 & 2a & -2c \\ -2a & 0 & 2b \\ 2c & -2b & 0 \\ \end{bmatrix}^T$

$=\begin{bmatrix} 0 & -2a & 2c \\ 2a & 0 & -2b \\ -2c & 2b & 0 \\ \end{bmatrix}$

となる。

これらの計算結果から、

$(A^T-A)^T=-(A^T-A)$

が成り立つため、交代行列であることが分かった。

2.4. 交代行列が固有値$\lambda$を持つとき$-\lambda$の固有値も持つ

まず、行列を転置したときに固有値は変わらないことを考える。

固有方程式は$\mathrm{det}(A-\lambda E)=0$となるが、$\mathrm{det}(A^T-\lambda E)=0$としたところで、対角成分は変わらないのに加えて、行と列が入れ替わっただけなので、固有値は変化しない。

$A\boldsymbol{x}=\lambda \boldsymbol{x}$より、$A^T\boldsymbol{x}$について考えると、

$A^T\boldsymbol{x}=-A \boldsymbol{x}$

$=-\lambda \boldsymbol{x}$

となるため、$-\lambda$の固有値も持つ。

---

固有方程式$\mathrm{det}(A-\lambda E)=0$を用いると、

$\mathrm{det}(A-\lambda E)$

$=\begin{vmatrix} -\lambda &-1\\ 1 &-\lambda \\ \end{vmatrix}$

$=\lambda^2+1=0$

となるため、$\lambda=\pm i$となる。

そのため、交代行列が固有値$i$を持つとき$-i$の固有値も持つことがわかる。

3. 対称行列と交代行列の性質

正方行列は対称行列と交代行列の和で表すことができます。

$A$を正方行列とする。

$A=\dfrac{1}{2}A+\dfrac{1}{2}A$

$=\dfrac{1}{2}A+\dfrac{1}{2}A+\dfrac{1}{2}A^T-\dfrac{1}{2}A^T$

$=\dfrac{1}{2}(A+A^T)+\dfrac{1}{2}(A-A^T)$

$A+A^T$は対称行列、$A-A^T$は交代行列であるから、正方行列は対称行列と交代行列の和で表すことができるということが分かった。