複素数平面と極形式の性質・例題について

1. 複素数平面
複素数平面は、ガウス平面や複素平面とも呼ばれることがあります。
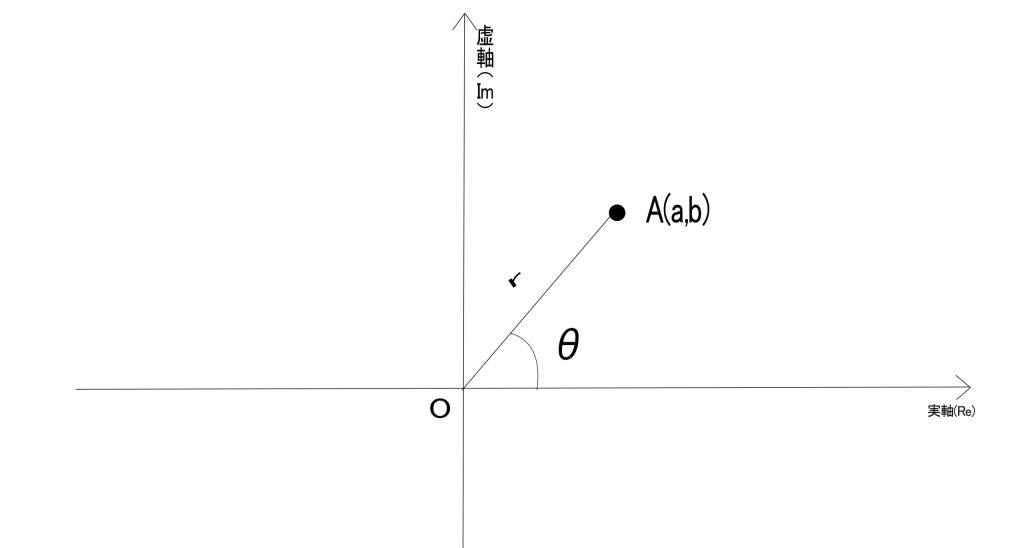
複素数 $z = a + bi$ は、$a$ が実数部分、$b$ が虚数部分で、$i$ は虚数単位を表しています。このとき、複素数 $z$ は座標平面上の点 $(a, b)$ に対応します。
具体的には、$x$ 軸が実数部分である実軸、$y$ 軸が虚数部分である虚軸を表しています。つまり、複素数平面では、複素数を2次元の座標として捉えることができ、実数部分 $a$ が $x$ 軸の値、虚数部分 $b$ が $y$ 軸の値になります。
例えば、複素数 $z = 3 + 4i$ であれば、平面上の点 $(3, 4)$ に対応し、実軸方向に 3、虚軸方向に 4 だけ離れた位置にあることがわかります。このように、複素数平面を使うことで、複素数を直感的に視覚化し、計算や解析がより容易になります。
2. 極形式
$$z=r(\cos\theta+i\sin\theta)$$
これを極形式と呼ぶ。
複素数 $z = a + bi$ を考えます。このとき、$r$ は原点から点 $(a, b)$ までの距離に相当します。すなわち、次のように定義されます。
\[ r = \sqrt{a^2 + b^2} \]
したがって、複素数 $z$ は極形式で次のように表されます。
\[ a + bi = \sqrt{a^2 + b^2} (\cos \theta + i \sin \theta) \]
ここで、偏角$\theta$ は複素数 $z$ が原点からなす角度を表し、次のような関係式が成り立ちます。
\[ \cos \theta = \frac{a}{\sqrt{a^2 + b^2}}, \quad \sin \theta = \frac{b}{\sqrt{a^2 + b^2}} \]
ただし、$a = 0$ かつ $b = 0$ の場合は除外します。以上の式から、$\cos \theta$ と $\sin \theta$ の絶対値がともに 1 以下であることを示す必要があります。
まず、$\cos \theta$ がこの条件を満たすかを確認しましょう。
2.1. $a > 0$ の場合
$a \neq 0$ で $a > 0$ のときを考えます。このとき、$\cos \theta$ は次のように計算されます。
\[ \cos \theta = \frac{a}{\sqrt{a^2 + b^2}} = \frac{1}{\sqrt{1 + \frac{b^2}{a^2}}} \]
ここで、$\frac{b^2}{a^2} \geq 0$ であるため、分母は 1 以上の値をとります。したがって、
\[ \cos \theta = \frac{1}{\sqrt{1 + \frac{b^2}{a^2}}} \leq 1 \]
このようにして、$|\cos \theta| \leq 1$ が成立することが確認できます。
2.2. $a = 0$ の場合
次に、$a = 0$ のときを考えます。この場合、$\cos \theta$ は次のようになります。
\[ \cos \theta = \frac{0}{\sqrt{0^2 + b^2}} = 0 \]
したがって、$|\cos \theta| = 0$ となり、条件 $|\cos \theta| \leq 1$ を満たします。
2.3. $a < 0$ の場合
最後に、$a \neq 0$ で $a < 0$ の場合を考えます。このとき、$\cos \theta$ は次のように計算されます。
\[ \cos \theta = \frac{a}{\sqrt{a^2 + b^2}} = -\frac{1}{\sqrt{1 + \frac{b^2}{a^2}}} \]
ここでも、$\frac{b^2}{a^2} \geq 0$ であるため、分母は 1 以上の値をとります。したがって、
\[ \cos \theta = -\frac{1}{\sqrt{1 + \frac{b^2}{a^2}}} \leq 1 \]
さらに、$\cos \theta = -\frac{1}{\sqrt{1 + \frac{b^2}{a^2}}} \geq -1$ であるため、
\[ |\cos \theta| \leq 1 \]
が成立します。
以上のように、$a$ の値にかかわらず、常に $|\cos \theta| \leq 1$ が成り立つことが確認されました。これにより、$\cos \theta$ が実際に $|\cos \theta| \leq 1$ の条件を満たしていることが示されました。
3. 極形式の例題
3.1. 例題 1: 複素数 \( z = 1 + i \) を極形式に変換
\( z \) の絶対値 \( r \) を求めます。 \[ r = |z| = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2} \]
偏角 \( \theta \) を求めます。$\sin\theta =\frac{\pi}{4},\cos\theta =\frac{\pi}{4}$より、偏角 \( \theta \) は次のようになります。
\[ \theta = \frac{\pi}{4} \]
極形式に変換します。
\[ z = r(\cos \theta + i \sin \theta) = \sqrt{2}\left(\cos \frac{\pi}{4} + i \sin \frac{\pi}{4}\right) \]
3.2. 例題 2: \( (1 + i)^2 \) の極形式への変換
\( (1 + i)^2 \) を展開します。
\[ (1 + i)^2 = (1 + i)(1 + i) \]
\[ = 1 \cdot 1 + 1 \cdot i + i \cdot 1 + i \cdot i \]
\[ 1 + i + i – 1 = 2i \]
ここで、複素数 \( 2i \) を極形式に直します。まず、絶対値 \( r \) を求めます: \[ r = |2i| = 2 \]
次に、偏角 \( \theta \) を求めます。複素数 \( 2i \) は虚軸上の正の方向にあるので、偏角は \( \frac{\pi}{2} \) です。
したがって、\( 2i \) の極形式は、
\[ 2i = 2\left(\cos \frac{\pi}{2} + i \sin \frac{\pi}{2}\right) \]