京都大学（理系）2025年度数学第1問解答解説

問題はご自身で探してください。

1. 問1（複素数）

複素数 \( z \) は絶対値が 2 なので、極形式で

\[ z = 2e^{i\theta} \quad (\theta \in [0, 2\pi)) \]

と表せます。このとき、逆数は

\[ \frac{1}{z} = \frac{1}{2e^{i\theta}} = \frac{1}{2} e^{-i\theta} \]

よって、式は以下のようになります：

\[ \left| z - \frac{i}{z} \right| = \left| 2e^{i\theta} - \frac{i}{2} e^{-i\theta} \right| \]

まず、オイラーの公式を使って、

\[ e^{i\theta} = \cos\theta + i\sin\theta,\quad e^{-i\theta} = \cos\theta - i\sin\theta \]

とすると：

\[ 2e^{i\theta} = 2\cos\theta + 2i\sin\theta \]

\[ \frac{i}{2} e^{-i\theta} = \frac{i}{2}(\cos\theta - i\sin\theta) = \frac{i\cos\theta}{2} + \frac{\sin\theta}{2} \]

したがって、

\[ z - \frac{i}{z} = 2\cos\theta + 2i\sin\theta - \left( \frac{\sin\theta}{2} + \frac{i\cos\theta}{2} \right) = \left(2\cos\theta - \frac{\sin\theta}{2} \right) + i\left(2\sin\theta - \frac{\cos\theta}{2} \right) \]

この複素数の絶対値は

\[ \left| z - \frac{i}{z} \right| = \sqrt{ \left(2\cos\theta - \frac{\sin\theta}{2} \right)^2 + \left(2\sin\theta - \frac{\cos\theta}{2} \right)^2 } \]

展開すると：

\[\begin{align*} & \sqrt{4\cos^2\theta - 2\cos\theta\sin\theta + \frac{\sin^2\theta}{4} + 4\sin^2\theta - 2\sin\theta\cos\theta + \frac{\cos^2\theta}{4}} \\ &= \sqrt{ \left(4\cos^2\theta + \frac{\cos^2\theta}{4}\right) + \left(4\sin^2\theta + \frac{\sin^2\theta}{4}\right) - 4\cos\theta\sin\theta } \\ &= \sqrt{ \frac{17}{4}(\cos^2\theta + \sin^2\theta) - 4\cos\theta\sin\theta } \\ &= \sqrt{ \frac{17}{4} - 4\cos\theta\sin\theta }\,. \end{align*}\]

２倍角の公式より、$\cos\theta\sin\theta = \frac{1}{2} \sin(2\theta)$なので：

\[ \left| z - \frac{i}{z} \right| = \sqrt{ \frac{17}{4} - 2\sin(2\theta) } \]

\(\sin(2\theta)\) の値域は \([-1, 1]\) なので：

• 最大値のとき：\(\sin(2\theta) = -1\)
  → \(\sqrt{\frac{17}{4} + 2} = \sqrt{\frac{25}{4}} = \frac{5}{2}\)
• 最小値のとき：\(\sin(2\theta) = 1\)
  → \(\sqrt{\frac{17}{4} - 2} = \sqrt{\frac{9}{4}} = \frac{3}{2}\)

2. 問2（積分）

2.1. (1) 分数の積分

分母が共通して \(x^2 + 1\) であることから、分子を項ごとに分けて次のように積分を分割できる。

\[ \frac{x\sqrt{x^2+1} + 2x^3 + 1}{x^2+1} = \frac{x\sqrt{x^2+1}}{x^2+1} + \frac{2x^3}{x^2+1} + \frac{1}{x^2+1} \]

したがって、元の積分は

\[ \int_0^{\sqrt{3}} \frac{x\sqrt{x^2+1}}{x^2+1}\,dx + \int_0^{\sqrt{3}} \frac{2x^3}{x^2+1}\,dx + \int_0^{\sqrt{3}} \frac{1}{x^2+1}\,dx \]

の3つの積分に分けられる。

最初の積分を考える。関数 \(\sqrt{x^2+1}\) の微分

\[ \left(\sqrt{x^2+1}\right)’ = \frac{x}{\sqrt{x^2+1}} \]

を利用して、

$$\begin{align*} \int_0^{\sqrt{3}} \frac{x\sqrt{x^2+1}}{x^2+1}\,dx &= \int_0^{\sqrt{3}} \frac{x}{\sqrt{x^2+1}}\,dx \\ &= \int_0^{\sqrt{3}} \left(\sqrt{x^2+1}\right)’\,dx \\ &= \left[\sqrt{x^2+1}\right]_0^{\sqrt{3}} \\ &= \sqrt{4} - \sqrt{1} \\ &= 2 - 1 \\ &= 1 \end{align*}$$

次に

\[ \int_0^{\sqrt{3}} \frac{2x^3}{x^2+1}\,dx \]

を計算する。分子の \(2x^3\) を工夫して、

\[ 2x^3 = 2x(x^2+1 - 1) = 2x(x^2+1) - 2x \]

と変形できるので、

\[ \frac{2x^3}{x^2+1} = 2x - \frac{2x}{x^2+1} \]

となる。したがって、積分は

\[ \int_0^{\sqrt{3}} \left(2x - \frac{2x}{x^2+1}\right) dx = \int_0^{\sqrt{3}} 2x\,dx - \int_0^{\sqrt{3}} \frac{2x}{x^2+1}\,dx \]

となる。前者は基本的な積分で、

\[ \int_0^{\sqrt{3}} 2x\,dx = \left[x^2\right]_0^{\sqrt{3}} = 3 \]

後者の積分は、分子が分母の導関数であるため、

\[ \int \frac{2x}{x^2+1}\,dx = \log(x^2 + 1) + C \]

より、定積分は

\[ \int_0^{\sqrt{3}} \frac{2x}{x^2+1}\,dx = \left[\log(x^2+1)\right]_0^{\sqrt{3}} = \log 4 - \log 1 = \log 4 \]

したがって、この部分の値は

\[ 3 - \log 4 \]

最後に

\[ \int_0^{\sqrt{3}} \frac{1}{x^2+1}\,dx \]

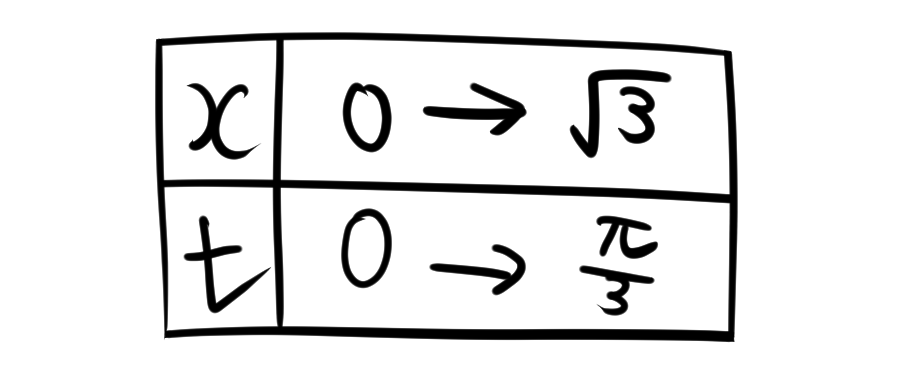
を計算する。\(x = \tan t\) と置けば、

積分区間は、\(x = 0\) のとき \(t = 0\)、\(x = \sqrt{3}\) のとき \(t = \frac{\pi}{3}\) なので、

\[ \begin{align*} &\int_0^{\sqrt{3}} \frac{1}{x^2+1}\,dx \\ &\int_0^{\sqrt{3}} \frac{1}{\tan^2 t+1}\,\frac{1}{cos^2 t} dt \\ &= \int_0^{\pi/3} dt\\ &= \frac{\pi}{3} \end{align*} \]

以上をすべて合計すると、

\[ 1 + (3 - \log 4) + \frac{\pi}{3} = 4 - \log 4 + \frac{\pi}{3} \]

したがって、与えられた積分の値は

\[ \boxed{4 - \log 4 + \dfrac{\pi}{3}} \]

2.2. (2) 三角関数の積分

半角の公式より

\[ 1 - \cos x = 2 \sin^2\left(\frac{x}{2}\right), \quad 1 + \cos x = 2 \cos^2\left(\frac{x}{2}\right) \]

これらを分数に代入すると、積分の中身は次のように変形されます。

\[ \sqrt{\frac{2 \sin^2\left(\frac{x}{2}\right)}{2 \cos^2\left(\frac{x}{2}\right)}} = \sqrt{\tan^2\left(\frac{x}{2}\right)} = \left|\tan\left(\frac{x}{2}\right)\right| \]

積分区間は \(x \in [0, \frac{\pi}{2}]\) なので、この区間では \(\tan\left(\frac{x}{2}\right)\) は常に正なので、絶対値を外すことができます。したがって積分は次のように書き換えられます。

\[ \begin{align*} \int_0^{\frac{\pi}{2}} \tan\left(\frac{x}{2}\right) dx &= \left[-2 \log \left| \cos\left(\frac{x}{2}\right) \right| \right]_0^{\frac{\pi}{2}} \\ &= -2 \log \left( \cos\left( \frac{\pi}{4} \right) \right) + 2 \log \left( \cos(0) \right) \\ &= -2 \log \left( \frac{\sqrt{2}}{2} \right) + 2 \log 1 \\ &= -2 \log \left( \frac{\sqrt{2}}{2} \right) \\ &= -2 \log \left( 2^{-1/2} \right) \\ &= -2 \cdot \left( -\frac{1}{2} \log 2 \right) \\ &= \log 2 \end{align*} \]

よって、積分の値は

\[ \boxed{\ln 2} \]