【ベクトル解析】ナブラ∇とラプラシアンの意味について

1. ナブラ∇
∇(ナブラ、あるいはデル)は、数学や物理学で使用される特別な記号で、多くの分野で役立つ概念です。この記号は、ベクトル演算の一種を表すもので、勾配、発散、回転といった計算に使われます。
1.1. ∇とベクトル
\[ \nabla = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right) \]
この形を見ると、∇は通常のベクトルと同じように \( x \) 軸、\( y \) 軸、\( z \) 軸方向の成分を持っていますが、それぞれの成分は「微分の操作」を意味しています。
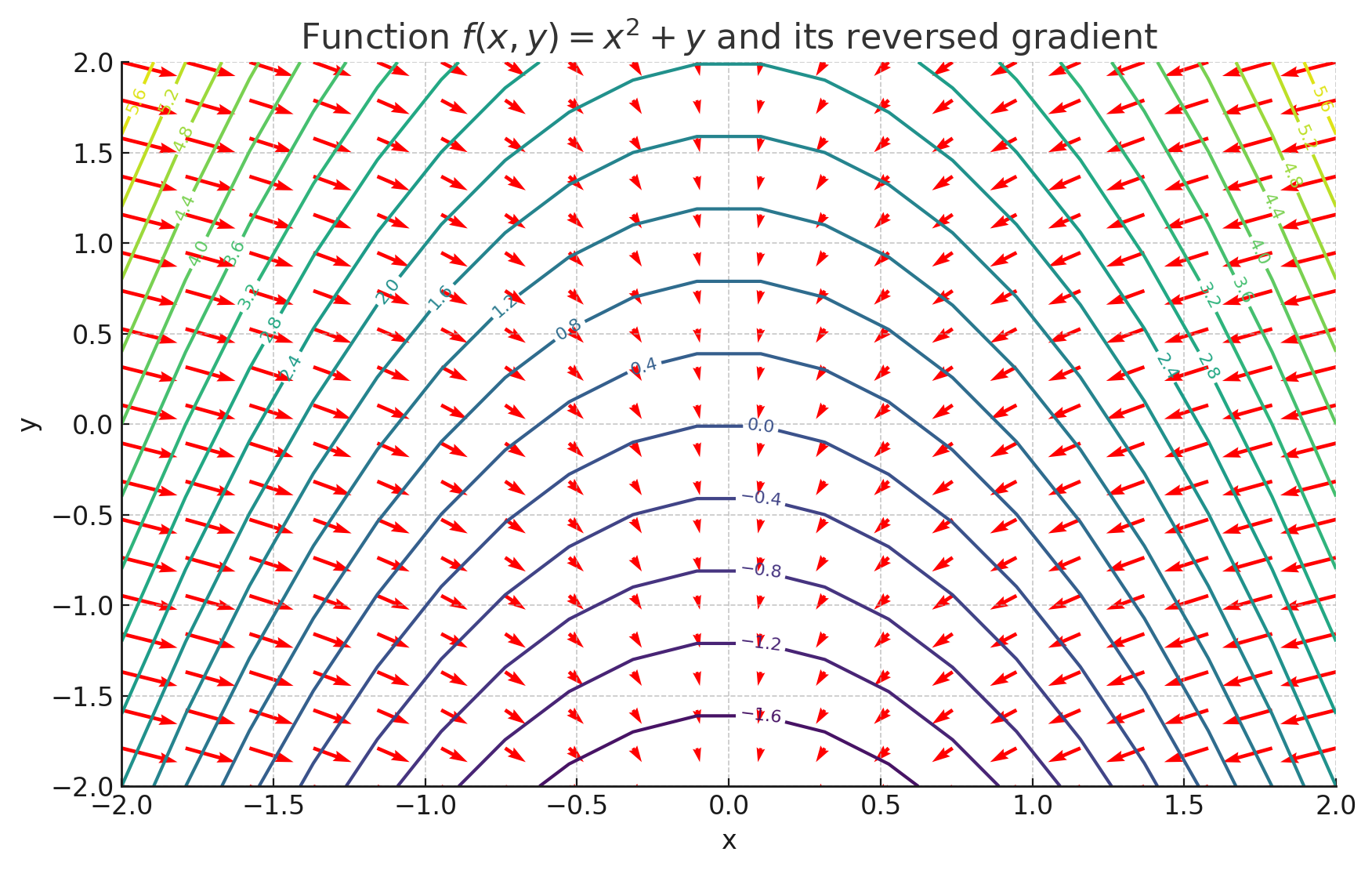
1.2. グラディエント(∇f)
スカラー場に対して∇を適用すると、勾配(グラディエント)と呼ばれるベクトルが得られます。
\[ \nabla f =\text{grad} \, f= \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right) \]
勾配は、特定の地点で値がどの方向に増加するかを示します。
1.3. ダイバージェンス(∇・F)
ベクトル場に対して∇を「・(ドット積)」とともに適用すると、その場がどれだけ「発散」しているかを示すスカラーが得られます。
\[ \nabla \cdot \mathbf{F}=\text{div} \, \mathbf F = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} \]
ダイバージェンスは、流れで言えば、ある地点で流体が「流れ出ている」か「流れ込んでいる」かを示します。
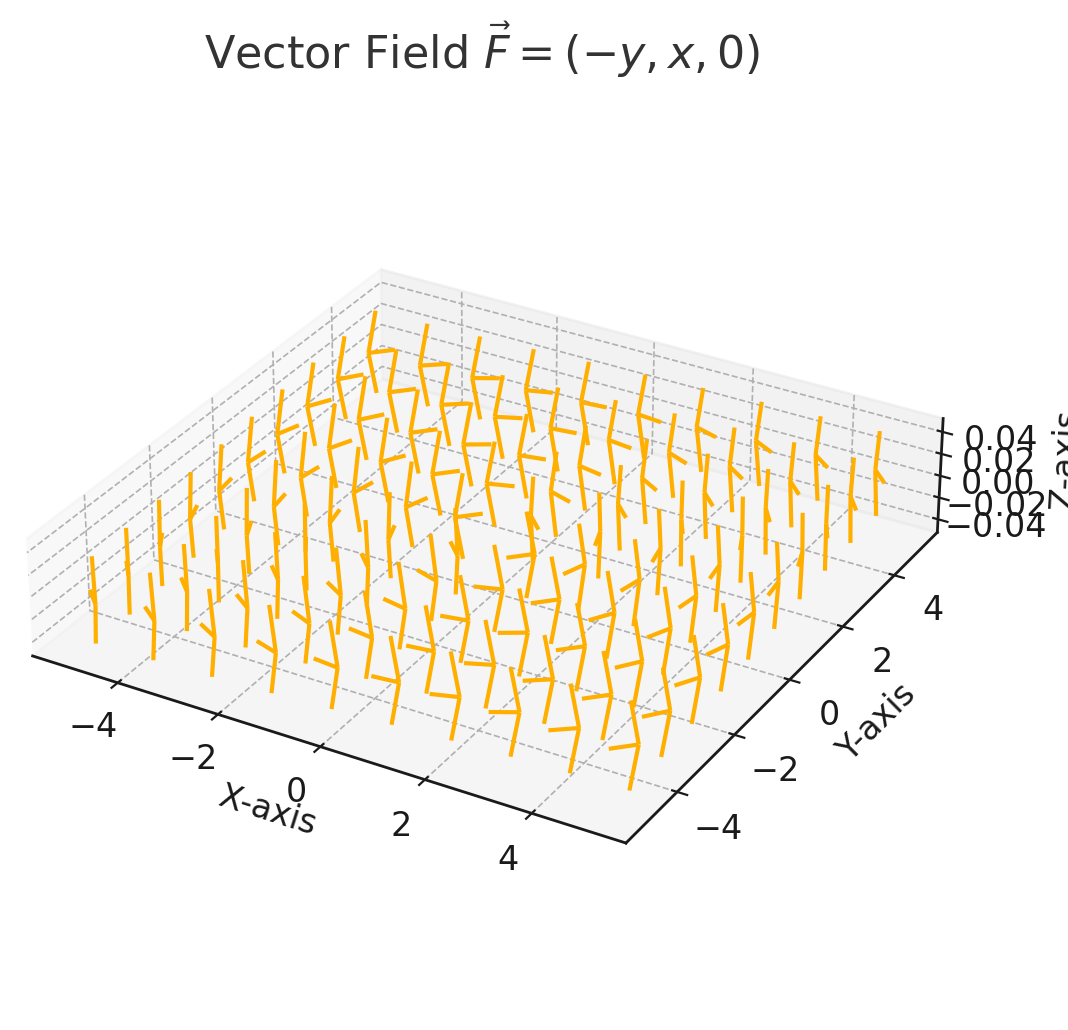
1.4. カール(∇×F)
ベクトル場に対して∇を「×(クロス積、外積)」とともに適用すると、その場の「回転」や「うねり」の強さを示すベクトルが得られます。
\[ \nabla \times \mathbf{F} =\text{rot} \, \mathbf F = \left( \frac{\partial F_z}{\partial y} – \frac{\partial F_y}{\partial z}, \frac{\partial F_x}{\partial z} – \frac{\partial F_z}{\partial x}, \frac{\partial F_y}{\partial x} – \frac{\partial F_x}{\partial y} \right) \]
回転は、特定の点でどの程度の回転があるかを示します。
2. ラプラス作用素
ラプラス作用素(Laplacian)は、数学や物理学において多くの応用を持つ微分演算子です。特に物理学での熱や波の伝播、電磁場の分布などを扱う際に重要です。ラプラス作用素は、関数のパラメーターの2階微分を合計したもので、多くの場合「$\nabla ^2$」や「$\Delta f$」と表記されます。
2.1. 2変数の場合
\[ \Delta f =\nabla ^2 f= \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} \]
この式では、$f$ の各変数 $x$ と $y$ に対して2階微分を行い、その結果を足し合わせています。
2.2. n変数の場合
\[ \Delta f =\nabla ^2 f= \frac{\partial^2 f}{\partial x_1^2} + \frac{\partial^2 f}{\partial x_2^2}+\cdots + \frac{\partial^2 f}{\partial x_n^2} \]
2.3. 微分演算子を利用した表現
$$\Delta f =\text{div} \, \text{grad} \, f $$
ラプラス作用素 \( \Delta f = \text{div} \, \text{grad} \, f \) を展開してみましょう。ここでは、勾配(grad)をまず計算し、それを発散(div)で再度適用することでラプラス作用素の展開を行います。まず、関数 \( f(x, y, z) \) に対して勾配 \(\text{grad} \, f\) を求めます。
$$ \text{grad} \, f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right) $$
次に、この勾配ベクトルに発散を適用します。発散は、勾配の各成分を再び微分し、それらを合計する操作です。したがって、ラプラス作用素は次のように展開されます。
$$ \Delta f = \text{div} \, \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right) = \frac{\partial}{\partial x} \left( \frac{\partial f}{\partial x} \right) + \frac{\partial}{\partial y} \left( \frac{\partial f}{\partial y} \right) + \frac{\partial}{\partial z} \left( \frac{\partial f}{\partial z} \right) $$
各成分の微分を計算して、最終的なラプラス作用素を次のように表せます。
$$ \Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2} $$
3. ラブラスの微分方程式
\[ \Delta f =0 \]
関数 は「調和関数」と呼ばれます。