ルジャンドルの定理の証明と具体例、例題について

はるか

ルジャンドルの定理って…階乗が素数で何回割り切れるか、を求める。

ふゅか

そうそう！例えば「10!が2で何回割れるか」とかね！

1. ルジャンドルの定理とは

1.1. 具体例

\( 10! \)を２で何回割ることができるか示す。

\[ \begin{align*} \sum_{k=1}^{\infty} \left\lfloor \frac{10}{2^k} \right\rfloor & = \left\lfloor \frac{10}{2} \right\rfloor + \left\lfloor \frac{10}{4} \right\rfloor + \left\lfloor \frac{10}{8} \right\rfloor \\ & = 5 + 2 + 1 \\ & = 8 \end{align*} \]

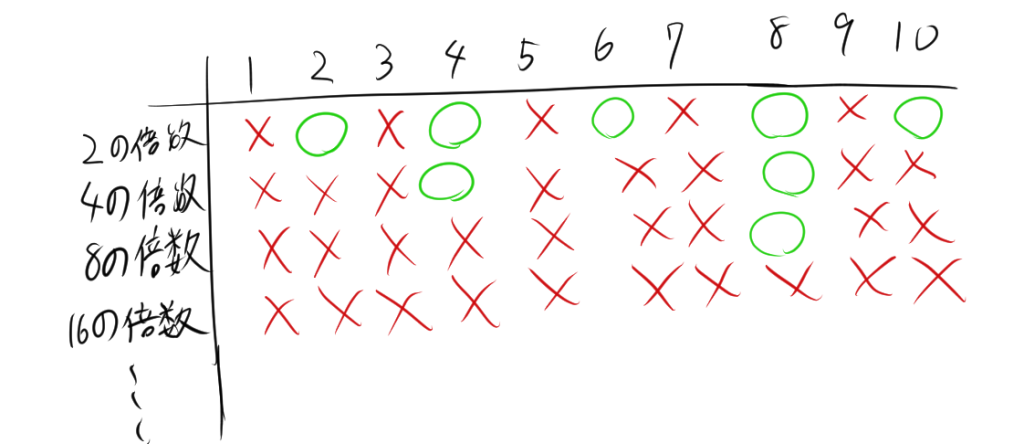
したがって、\( 10! \)は2で8回割ることができます。表にして可視化するとつぎのようになります。

1.2. 証明

1.2.1. \( p \) の倍数を数える

まず、\( n! \) は \( 1 \) から \( n \) までのすべての整数の積です。\( n! \) に含まれる \( p \) のべき乗の数を数えるために、\( 1 \) から \( n \) の間に \( p \) の倍数がいくつあるかを考えます。

整数 \( 1, 2, 3, \dots, n \) のうち、\( p \) の倍数は次のように数えられます。

\[ \left\lfloor \frac{n}{p} \right\rfloor \]

この数は、\( n! \) の中に含まれる \( p \) の1乗の数を表しています。

1.2.2. \( p^2 \) の倍数を数える

次に、\( n! \) の中に含まれる \( p^2 \) の倍数、すなわち \( p^2 \) の因子の数を考えます。\( p^2 \) の倍数は次のように数えられます。

\[ \left\lfloor \frac{n}{p^2} \right\rfloor \]

つまり、ここでは、pで２回割ることができる数を探しています。

はるか

すでに、pが１回割れる数として先ほど計算しているので、2回たさずに一回たせばいい。

1.2.3. 繰り返す

同様に、\( p^3 \) の倍数、\( p^4 \) の倍数、…をそれぞれ数えることができます。これを一般化すると、\( p^i \) の倍数の数は次のように表されます。

\[ \left\lfloor \frac{n}{p^i} \right\rfloor \]

1.2.4. 和の打ち切り

はるか

そうやって、p³、p⁴…も順番に数える。

ふゅか

でもね、永遠に続くわけじゃなくて、ある時点で終わるの。\( p^i \)がnより大きくなると、そこで打ち切り！

ただし、和は無限に続くわけではなく、\( p^i \) が \( n \) より大きくなると、\( \left\lfloor \frac{n}{p^i} \right\rfloor = 0 \) となり、それ以上加算する必要がなくなります。したがって、この和は有限回の項で打ち切られます。

以上のステップを通して、\( n! \) に含まれる素数 \( p \) で割ることができる回数kは次のように表すことができる。

\[ k = \sum_{i=1}^{\infty} \left\lfloor \frac{n}{p^i} \right\rfloor \]

2. 例題

\[ \left\lfloor \frac{100}{5} \right\rfloor + \left\lfloor \frac{100}{25} \right\rfloor = 20 + 4 = 24 \]

ルジャンドルの定理を用いることで、\( 100! \)は5で\( 24 \)回割り切れることが分かります。