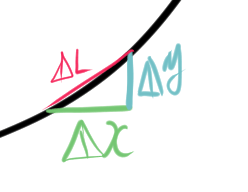曲線の長さを求める方法・y=f(x)・媒介変数表示・極方程式について

1. $y=f(x)$を用いた表現
$$L = \int_a^b \sqrt{1 + (f'(x))^2} \, dx$$
曲線の長さを求めるためには、まず曲線を小さな線分に分割し、それぞれの長さを近似的に求めてから、それらの長さを合計する方法をとります。
微小区間 $[x,x+\Delta x]$について考える。
微小な曲線の長さを$\Delta L$とすると、
$$\Delta L \fallingdotseq \sqrt{(\Delta x)^2+(\Delta y)^2}$$
したがって、
$$\Delta L \fallingdotseq \sqrt{(1+\left(\frac{\Delta y}{\Delta x}\right)^2}\Delta x$$
$$\frac{\Delta L}{\Delta x} \fallingdotseq \sqrt{(1+\left(\frac{\Delta y}{\Delta x}\right)^2}$$
となる。
ここで、$\Delta x$を限りなく0に近づけると、$\frac{\Delta y}{\Delta x}$は関数$f(x)$の導関数$f'(x)$となるので、
$$\frac{dL}{dx} = \sqrt{1 + (f'(x))^2}$$
よって、曲線の長さ$L$は次のようになる。
$$L = \int_a^b \frac{dL}{dx} \, dx = \int_a^b \sqrt{1 + (f'(x))^2} \, dx$$
1.1. y=f(x)の形の曲線を求める例題
$$y= x$$
この場合、導関数 \( y’ = 1 \) です。曲線の長さの公式に代入すると、
\[ L = \int_0^1 \sqrt{1 + (y’)^2} \, dx = \int_0^1 \sqrt{1 + 1^2} \, dx = \int_0^1 \sqrt{2} \, dx \]
\[ L = \sqrt{2} \times (1 – 0) = \sqrt{2} \]
2. 媒介変数による表現
$$L = \int_a^b \sqrt{\left(\frac{dx}{d\theta}\right)^2+\left(\frac{dy}{d\theta}\right)^2} \, d\theta$$
$x(\theta)、y(\theta)$は$\theta$で微分可能、$\frac{dx}{d\theta}.\frac{dy}{d\theta}$は連続であるとする。
媒介変数表示で積分の計算が成り立つことを示す。
\[ dx = x'(\theta) d\theta, \quad dy = y'(\theta) d\theta \]
これを距離の公式に代入して、
\[
dL = \sqrt{(dx)^2 + (dy)^2} = \sqrt{(x'(\theta) d\theta)^2 + (y'(\theta) d\theta)^2}
\]
ここで、\(d\theta\) を括り出して整理すると、
\[
dL = \sqrt{x'(\theta)^2 + y'(\theta)^2} \, d\theta
\]
ここで曲線の全長 \(L\) は、この微小距離 \(dL\) を \(\theta\) の範囲 \(a\) から \(b\) まで積分して求めます。
\[
L = \int_a^b \sqrt{\left(\frac{dx}{d\theta}\right)^2+\left(\frac{dy}{d\theta}\right)^2} \, d\theta
\]
3. 極方程式による表現
$$L = \int_a^b \sqrt{r^2+\left(\frac{dr}{d\theta}\right)^2} \, d\theta $$
極座標変換を行うため、$x=r\cos\theta,y=r\sin\theta$と置きます。$\theta$で微分すると次のようになります。
$$\frac{dx}{d\theta} = \frac{dr}{d\theta}\cos\theta -r\sin\theta$$
$$\frac{dy}{d\theta} = \frac{dr}{d\theta}\sin\theta + r\cos\theta$$
まず、\(\left(\dfrac{dx}{d\theta}\right)^2\) と \(\left(\dfrac{dy}{d\theta}\right)^2\) をそれぞれ計算します。
1. \(\dfrac{dx}{d\theta} = \dfrac{dr}{d\theta}\cos\theta – r\sin\theta\)
\[ \left(\dfrac{dx}{d\theta}\right)^2 = \left(\dfrac{dr}{d\theta}\cos\theta – r\sin\theta\right)^2 = \left(\dfrac{dr}{d\theta}\right)^2\cos^2\theta – 2r\dfrac{dr}{d\theta}\cos\theta\sin\theta + r^2\sin^2\theta \]
2. \(\dfrac{dy}{d\theta} = \dfrac{dr}{d\theta}\sin\theta + r\cos\theta\)
\[ \left(\dfrac{dy}{d\theta}\right)^2 = \left(\dfrac{dr}{d\theta}\sin\theta + r\cos\theta\right)^2 = \left(\dfrac{dr}{d\theta}\right)^2\sin^2\theta + 2r\dfrac{dr}{d\theta}\cos\theta\sin\theta + r^2\cos^2\theta \]
次に、これらを足し合わせます。
\[ \left(\dfrac{dx}{d\theta}\right)^2 + \left(\dfrac{dy}{d\theta}\right)^2 = \left(\dfrac{dr}{d\theta}\right)^2(\cos^2\theta + \sin^2\theta) + r^2(\sin^2\theta + \cos^2\theta) \]
ここで、\(\cos^2\theta + \sin^2\theta = 1\) なので、
\[ \left(\dfrac{dx}{d\theta}\right)^2 + \left(\dfrac{dy}{d\theta}\right)^2 = \left(\dfrac{dr}{d\theta}\right)^2 + r^2 \]
したがって、媒介変数表示の曲線の長さより、曲線Lの長さは次のようになります。
$$L = \int_a^b \sqrt{r^2+\left(\frac{dr}{d\theta}\right)^2} \, d\theta $$
4. 曲線の長さを求める例題
4.1. \( y = f(x) \) の例題
曲線の長さ \( L \) は次の公式で与えられます。
\[ L = \int_{a}^{b} \sqrt{1 + \left( \frac{dy}{dx} \right)^2} \, dx \]
まず、関数 \( y = x^2 \) の導関数 \( \frac{dy}{dx} \) を求めます。
\[ \frac{dy}{dx} = 2x \]
次に、媒介変数表示の長さの公式に代入します。
\[ L = \int_0^1 \sqrt{1 + (2x)^2} \, dx = \int_0^1 \sqrt{1 + 4x^2} \, dx \]
この積分を計算していきましょう。
まず、次の積分を考えます。
\[ \int_0^1 \sqrt{1 + 4x^2} \, dx \]
\[ = 2\int_0^1 \sqrt{x^2 + \frac{1}{4}} \, dx \]
ここで、部分積分を利用して計算を進めます。計算結果は次のようになります。
\[ = 2 \cdot \frac{1}{2} \left[ x\sqrt{x^2 + \frac{1}{4}} + \frac{1}{4} \log\left(x + \sqrt{x^2 + \frac{1}{4}}\right) \right]_0^1 \]
これをさらに整理して、定積分の結果を求めると次のようになります。
\[ = \sqrt{\frac{5}{4}} + \frac{1}{4} \log\left(1 + \sqrt{\frac{5}{4}}\right) – \frac{1}{4} \log \frac{1}{2} \]
さらに簡潔にすると、
\[ = \frac{\sqrt{5}}{2} + \frac{1}{4} \log\left(1 + \frac{\sqrt{5}}{2}\right) + \frac{1}{4} \log 2 \]
\[ = \frac{\sqrt{5}}{2} + \frac{1}{4} \log(2 + \sqrt{5}) \]
したがって、曲線の長さ \(L\) は以下の通りです。
\[ L = \frac{\sqrt{5}}{2} + \frac{1}{4} \log(2 + \sqrt{5}) \]
4.2. 媒介変数表示の例題
曲線の長さ \( L \) は次の公式で与えられます。
\[ L = \int_{t_1}^{t_2} \sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2} \, dt \]
まず、各導関数を求めます。
\[ \frac{dx}{dt} = -\sin t, \quad \frac{dy}{dt} = \cos t \]
したがって、長さの公式は次のようになります。
\[ L = \int_0^{\frac{\pi}{2}} \sqrt{(-\sin t)^2 + (\cos t)^2} \, dt = \int_0^{\frac{\pi}{2}} \sqrt{\sin^2 t + \cos^2 t} \, dt = \int_0^{\frac{\pi}{2}} 1 \, dt \]
積分の結果は
\[ L = \frac{\pi}{2} \]
4.3. 極方程式の例題
曲線の長さ \( L \) は次の公式で与えられます。
\[ L = \int_{\theta_1}^{\theta_2} \sqrt{r^2 + \left( \frac{dr}{d\theta} \right)^2} \, d\theta \]
まず、\( r = 2\sin \theta \) の導関数 \( \frac{dr}{d\theta} \) を求めます。
\[ \frac{dr}{d\theta} = 2\cos \theta \]
したがって、長さの公式は次のようになります。
\[ L = \int_0^{\pi} \sqrt{(2\sin \theta)^2 + (2\cos \theta)^2} \, d\theta = \int_0^{\pi} \sqrt{4\sin^2 \theta + 4\cos^2 \theta} \, d\theta = \int_0^{\pi} \sqrt{4} \, d\theta = \int_0^{\pi} 2 \, d\theta \]
積分の結果は
\[ L = 2\pi \]