一次方程式ax + b = 0の解き方と一次関数との関係、3つの例題について

はるか

一次方程式は$ax + b = 0$の形。

ふゅか

うん！一見簡単に見えるけど、ちゃんと移項とか割り算をしっかり理解することが大事だよね！

1. 一次方程式

ここで、$a$ と $b$ は定数で、$a\neq 0$、$x$ は未知数です。

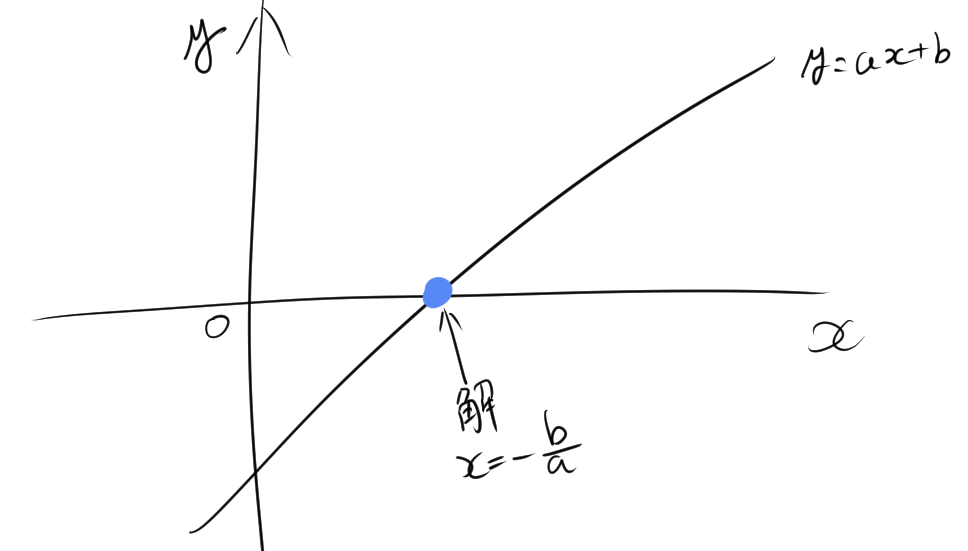
1.1. 一次方程式と一次関数の関係

一次方程式の解は、一次関数がy=0のときのxの値になります。

2. 一次方程式を解く手順

一次方程式を解く手順は以下の通りです。

2.1. 移項

$x$ の項を一方の辺に集め、定数をもう一方に移項します。例えば、次の方程式の場合。

\[ 2x + 3 = 7 \]

まず、$3$ を移項します。これには、両辺から $3$ を引きます。

\[ 2x = 4 \]

2.2. $x$ の係数で両辺を割る

次に、$x$ の係数  で両辺を割ります。この場合、両辺を $2$ で割ります。

\[ x = 2 \]

これで解が得られました。

3. 例題

3.1. 例題 1

$-5$ を右辺に移項します（両辺に $5$ を足します）\[ 3x = 15 \]

両辺を $3$ で割ります \[ x = 5 \]

したがって、解は $x = 5$ です。

3.2. 例題 2

$8$ を右辺に移項します（両辺から $8$ を引きます） \[ 4x = -8 \]

両辺を $4$ で割ります \[ x = -2 \]

したがって、解は $x = -2$ です。

3.3. 例題 3

$3$ を右辺に移項します（両辺から $3$ を引きます） \[ -5x = -10 \]

両辺を $-5$ で割ります \[ x = 2 \]

したがって、解は $x = 2$ です。