一次不等式と数直線による可視化、例題ついて

1. 一次不等式と数直線

不等式の解を視覚的に示すときに数直線を使います。例えば、\( x > 2 \) の場合、2 より大きい数の範囲を数直線上に描くことで、解の範囲を視覚的に表現できます。

2. 数直線

数直線とは、数の位置関係を視覚的に表すための直線のことです。通常は水平に描かれ、直線上の点が数の位置に対応します。数直線は、数の大小関係や範囲を理解するのに役立ちます。

2.1. 数直線の基本的な特徴

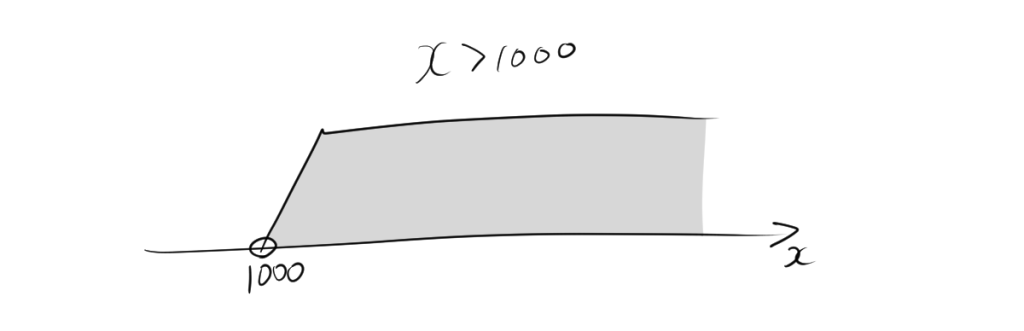
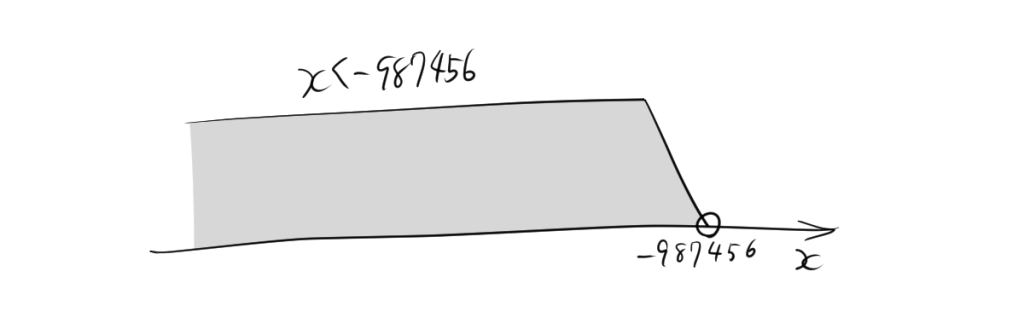
2.2. 不等号にイコールを含まない場合

不等号にイコールを含まない場合の数直線は次のように書かれます。

$x>1000$の場合

$x<-987456$の場合

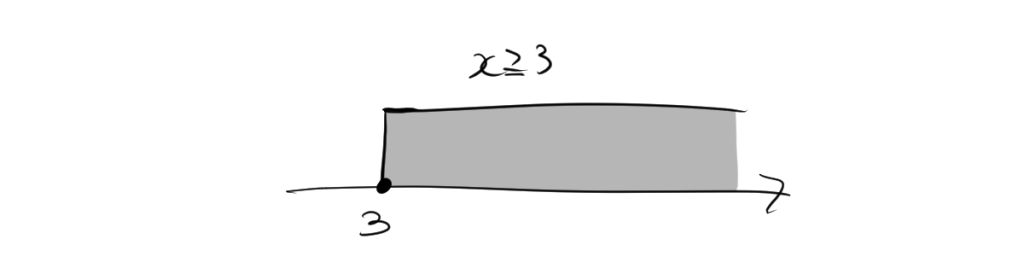
2.3. 不等号にイコールを含む場合

不等号にイコールを含む場合の数直線は次のように書かれます。

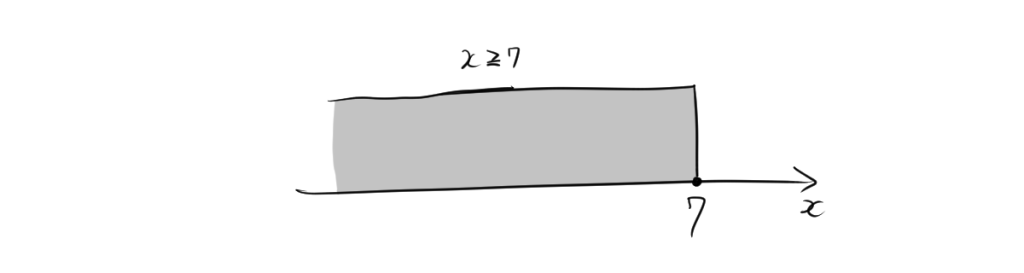
$x\geqq 3$の場合

$x\leqq 7$の場合

3. 例題

3.1. 不等式を解く

まず、不等式を通常の方程式のように扱い、x の値を求めます。

\[ 2x – 5 > 3 \]

この不等式を解くために、以下の手順に従います。

5を移項すると（両辺に 5 を足します）。

\[ 2x > 8 \]

両辺を 2 で割ります。

\[ x > 4 \]

これで、x は 4 より大きいという不等式が得られました。

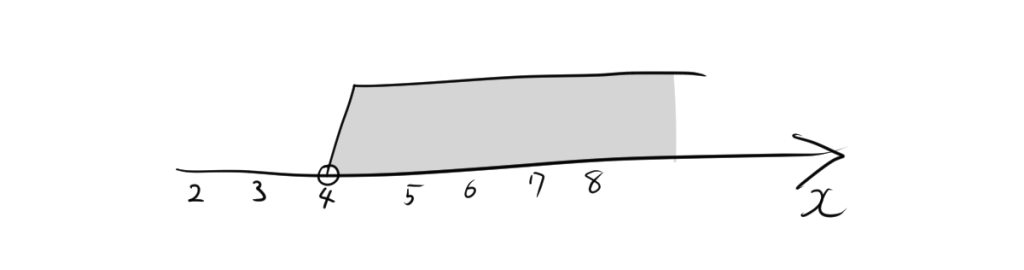
3.2. 数直線を描く

次に、数直線を描きます。数直線上に重要な点（この場合は 4）を示し、その周りにいくつかの数を配置します。

• 点 4 の位置に 白丸をつけます（これが 4 を含まないことを示します）。

この数直線上で、求めた範囲 \(x > 4\) を表現します。

3.3. 解の確認

最後に、いくつかの具体的な解が正しいか確認しましょう。

• \(x = 5\) の場合：数直線より右側に存在するため、不等式の範囲内に含まれる。
• \(x = 3\) の場合：数直線より左側に存在するため、不等式の範囲内に含まれない。

4. どうのような場合に使うのか？

数直線は、複数の不等式や連立不等式の解を視覚的に示す場合に非常に役立ちます。特に、不等式が複数あり、それらの解がどう重なり合うか、どの範囲が共通しているのかを確認するために用いると効果的です。以下は、数直線を使う具体的な場合について説明します。

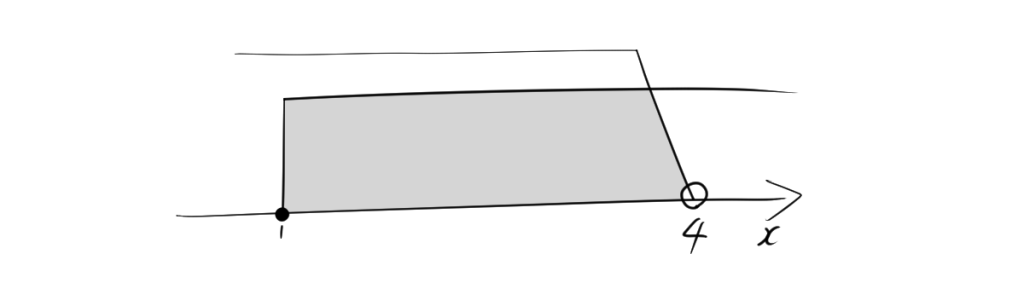
例えば、次の不等式を考えてみましょう。

\[ x \geqq 1 \quad \text{かつ} \quad x < 4 \]

この場合、数直線を使ってそれぞれの不等式の解を描き、その重なり合う部分が最終的な解となります。