【図形と方程式】軌跡と点の集合、3つの例題について

1. 軌跡
軌跡とは、特定の条件を満たしながら動く点の集合のことを指します。言い換えると、ある条件下で可能なすべての点の場所を集めたものです。
1.1. 軌跡の求め方
動いている点(動点)の座標を \( X \) と \( Y \) とします。
2. 条件に基づいて式を作成する
与えられた条件をもとに、\( X \) と \( Y \) を使って方程式を立てます。これにより、動点が満たすべき関係を明確にします。
3. 定義域や除外点に注意する
定義域(\( X \) や \( Y \) が取り得る値の範囲)や除外すべき点に注意してください。例えば、分母がゼロになる点や平方根の中が負になる点は除外します。
4. 図形と一緒に方程式を示す
最終的に、$(X,Y)$を$(x,y)$に置き換えて、求めた方程式とそれに対応する図形を一緒に示します。
2. 例題
2.1. 例題1:動点と円
動点の座標を \( P(X, Y) \) とします。まず、\( A(0, 0) \) と動点 \( P(X, Y) \) の距離 \( AP^2 \) は以下のように表せます。
\[ AP^2 = X^2 + Y^2 \]
次に、点 \( B(12, 12) \) との距離 \( BP \) は以下のように表せます。
\[ BP^2 = (X – 12)^2 + (Y – 12)^2 \]
この2つの結果を \( AP^2 + BP^2 = 144 \) に代入します。
\[ X^2 + Y^2 + (X – 12)^2 + (Y – 12)^2 = 288 \]
展開すると、
\[ X^2 + Y^2 + (X^2 – 24X + 144) + (Y^2 – 24Y + 144) = 288 \]
これを簡単にすると、
\begin{align*}
2X^2 + 2Y^2 – 24X – 24Y + 288 &= 288\\
2X^2 + 2Y^2 – 24X – 24Y &= 0 \\
X^2 + Y^2 – 12X – 12Y&= 0
\end{align*}
したがって、
\[ (X – 6)^2 + (Y – 6)^2 = 72 \]
動点 \( P\) の軌跡は、中心 \( (6, 6) \)、半径 \( 6\sqrt{2} \) の円を表します。また、求める軌跡は
\[ (x – 6)^2 + (y – 6)^2 = 72 \]
2.2. 例題2:動点と中点
まず、点 \( A(1, 0) \) と点 \( Q(x, y) \) の中点 \( P(X,Y) \) の座標を計算します。中点の公式より、点 \( P \) の座標は次のように表されます。
\[ \left( X, Y \right) = \left( \frac{x + 1}{2}, \frac{y}{2} \right) \]
次に、点 \( Q(x, y) \) が円 \( x^2 + y^2 = 1 \) 上にあるという条件を使います。この条件により、\( x \) と \( y \) は次の式を満たします。
\[ x^2 + y^2 = 1 \]
ここで、
\[ x = 2X – 1, \quad y = 2Y\]
円の方程式 \( x^2 + y^2 = 1 \) に代入します。
\[ (2X – 1)^2 + (2Y)^2 = 1 \]
両辺を4であると、
\[ (X- \frac{1}{2})^2 +Y^2 = \frac{1}{4} \]
中心が \( \left( \frac{1}{2}, 0 \right) \)、半径が \( \frac{1}{2} \) の円の方程式です。また、点 \( A(1, 0) \) と点 \( Q(1, 0) \) の場合は、線分の中点ではないので、除外する必要があります。したがって、点 \( P \) の軌跡は、中心 \( \left( \frac{1}{2}, 0 \right) \)、半径 \( \frac{1}{2} \) の円です。ただし、$(1,0)$を除く。
2.3. 例題3:動点と重心
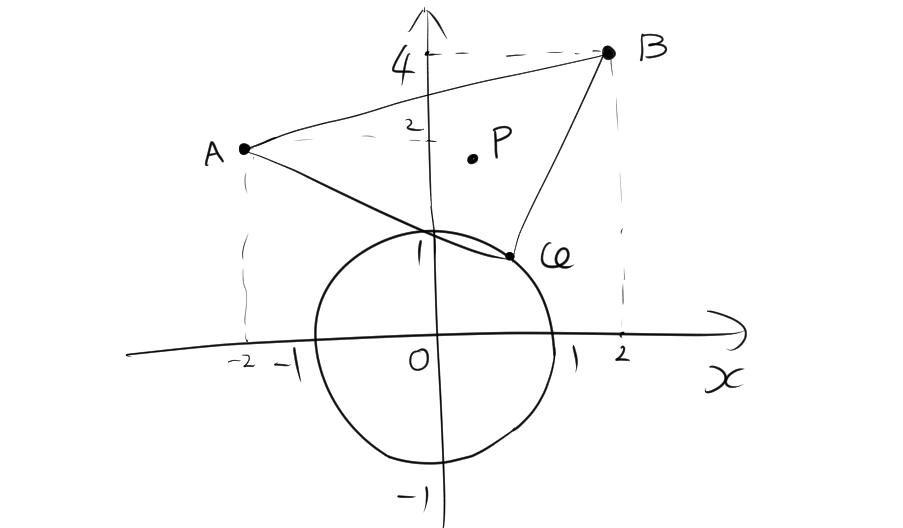
$\triangle ABQ$の重心の軌跡を求めなさい。
この問題は、点 \( A(-2,2) \)、点 \( B(2,4) \)、および円 \( x^2 + y^2 = 1 \) 上の点 \( Q(x_Q, y_Q) \) を頂点とする三角形 \( \triangle ABQ \) の重心の軌跡を求めるものです。
まず、重心 \( P(x_P, y_P) \) の座標は、三角形の3つの頂点の座標の平均として求められます。
\[
x_P = \frac{-2 + 2 + x_Q}{3} = \frac{x_Q}{3}
\]
\[
y_P = \frac{2 + 4 + y_Q}{3} = \frac{6 + y_Q}{3}
\]
これにより、重心 \( P(x_P, y_P) \) の座標は次のようになります。
\[ x_P = \frac{x_Q}{3}, \quad y_P = \frac{6 + y_Q}{3} \]
次に、点 \( Q \) が円 \( x^2 + y^2 = 1 \) 上にあるため、次の条件を満たします。
\[ x_Q^2 + y_Q^2 = 1 \]
この \( x_Q \) と \( y_Q \) を用いて、重心の軌跡を導きます。まず、\( x_Q = 3x_P \) 、\( y_Q = 3y_P – 6 \) と変形できます。これを上の式に代入します。
\[ 9x_P^2 + (3y_P – 6)^2 = 1 \]
\[ 9x_P^2 + 9(y_P – 2)^2 = 1 \]
両辺を9で割ります。
\[ x_P^2 + (y_P – 2)^2 = \frac{1}{9} \]
したがって、重心 \( P(x_P, y_P) \) の軌跡は、中心が \( (0, 2) \)、半径が \( \frac{1}{3} \) の円となります。