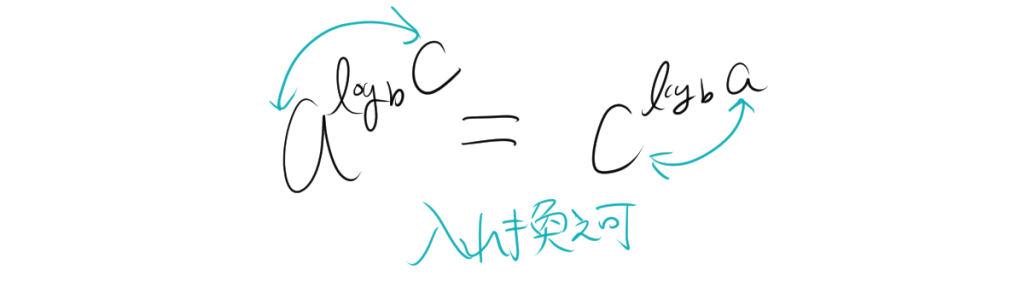【時間短縮】よく使われる対数の公式の計算例と証明について

- 1. 対数でよく使われる公式
- 2. 公式の証明
- 2.1. \( a^{\log_b c} = c^{\log_b a} \)の証明
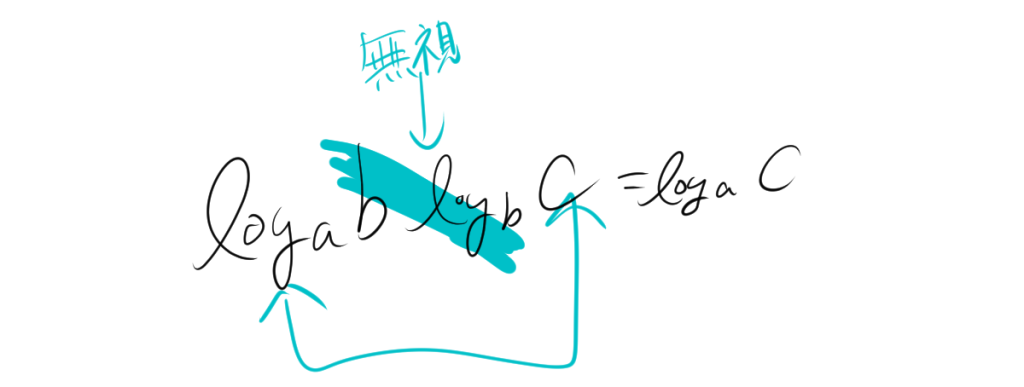
- 2.2. \( (\log_a b)(\log_b c) = \log_a c \)の証明
- 2.3. \( \log_{a^n} b = \dfrac{1}{n} \log_a b \)の証明
- 2.4. \( \log_a b = \dfrac{1}{\log_b a} \)の証明
- 3. 計算例
- 3.1. 例1:$a^{\log_b c} = c^{\log_b a}$
- 3.2. 例2:$(\log_a b)(\log_b c) = \log_a c$
- 3.3. 例3:$\log_{a^n} b = \frac{1}{n} \log_a b$
- 3.4. 例4:$\log_a b = \frac{1}{\log_b a}$
1. 対数でよく使われる公式
対数では、時間短縮のために次の公式が利用されることがある。
$$ \begin{align*}a^{\log_b c} &= c^{\log_b a} \\ (\log_a b)(\log_b c) &= \log_a c \\ \log_{a^n} b &= \frac{1}{n} \log_a b \\ \log_a b &= \frac{1}{\log_b a} \end{align*}$$
2. 公式の証明
2.1. \( a^{\log_b c} = c^{\log_b a} \)の証明
$(\log_b c)(\log_b a)$の積の順序を変えた等式
$$(\log_b c)(\log_b a) = (\log_b a)(\log_b c)$$
が成り立つ。対数の性質より、
$$(\log_b a^{\log_b c}) = (\log_b c^{\log_b a})$$
真数が等しいので、
$$a^{\log_b c}=c^{\log_b a}$$
2.2. \( (\log_a b)(\log_b c) = \log_a c \)の証明
対数の底の変換公式を使います。
$$ \log_b c = \dfrac{\log_a c}{\log_a b} $$
したがって、
\[ (\log_a b)(\log_b c) = (\log_a b) \left( \dfrac{\log_a c}{\log_a b} \right) = \log_a c \]
2.3. \( \log_{a^n} b = \dfrac{1}{n} \log_a b \)の証明
対数の底の変換公式を使います。
\[ \log_{a^n} b = \dfrac{\log_a b}{\log_a a^n}=\frac{1}{n}\log_a b \]
2.4. \( \log_a b = \dfrac{1}{\log_b a} \)の証明
底の変換公式を用いて変形します。
\[ \log_a b = \frac{\log_b b}{\log_b a} = \frac{1}{\log_b a} \]
3. 計算例
3.1. 例1:$a^{\log_b c} = c^{\log_b a}$
\[ 2^{\log_4 8} = 8^{\log_4 2} \]
まずは各対数を求めます。
- \(\log_4 8 = \frac{\log 8}{\log 4} = \frac{3 \log 2}{2 \log 2} = \frac{3}{2}\)
- \(\log_4 2 = \frac{\log 2}{\log 4} = \frac{\log 2}{2 \log 2} = \frac{1}{2}\)
それぞれ代入して計算します。
\[ 2^{\frac{3}{2}} = \sqrt{2^3} = \sqrt{8} = 2\sqrt{2} \]
\[ 8^{\frac{1}{2}} = \sqrt{8} = 2\sqrt{2} \]
両辺が等しいことがわかります。
3.2. 例2:$(\log_a b)(\log_b c) = \log_a c$
\[ (\log_2 8)(\log_8 64) = \log_2 64 \]
まずは各対数を求めます。
- \(\log_2 8 = 3\)
- \(\log_8 64 = \frac{\log 64}{\log 8} = \frac{6 \log 2}{3 \log 2} = 2\)
- \(\log_2 64 = 6\)
左辺
\[ (\log_2 8)(\log_8 64) = 3 \times 2 = 6 \]
右辺
\[ \log_2 64 = 6 \]
両辺が等しいことが確認できます。
3.3. 例3:$\log_{a^n} b = \frac{1}{n} \log_a b$
\[ \log_{3^2} 9 = \frac{1}{2} \log_3 9 \]
まずは各対数を求めます。
- \(\log_3 9 = 2\)
左辺
\[ \log_9 9 = 1 \]
右辺
\[ \frac{1}{2} \times 2 = 1 \]
両辺が等しいことがわかります。
3.4. 例4:$\log_a b = \frac{1}{\log_b a}$
\[ \log_2 8 = \frac{1}{\log_8 2} \]
まずは各対数を求めます。
- \(\log_2 8 = 3\)
- \(\log_8 2 = \frac{1}{3}\)
右辺
\[ \frac{1}{\log_8 2} = \frac{1}{\frac{1}{3}} = 3 \]
両辺が等しいことが確認できます。