対数不等式とは？解き方や2つの例題について
1. 対数不等式とは？
たとえば、「\(\log_a x > b\)」や「\(\log_a (x^2 + 1) \leq 3\)」といった形が対数不等式にあたります。対数方程式とは異なり、不等式です。
2. 対数不等式の基本的な解き方
対数不等式を解くには、まず対数の基本的な性質を理解しておくことが大切です。特に次のポイントを覚えておくと、不等式を解く際に役立ちます。$\log_a x$のとき、
底が \(0 < a < 1\)
したがって、真数が$x_1>x_2$のとき、
$$\log_a{x_1} < \log_a{x_2}$$
底が \(a>1\)
したがって、真数が$x_1>x_2$のとき、
$$\log_a{x_1} > \log_a{x_2}$$
このように、指数不等式と同様に、不等号が変化します。したがって、基本的な解き方をまとめると
- 変数の範囲を確認。
- 底を揃える。
- 必要であれば、置換。
- 真数を比較。底によって符号が変わる。
3. 例題
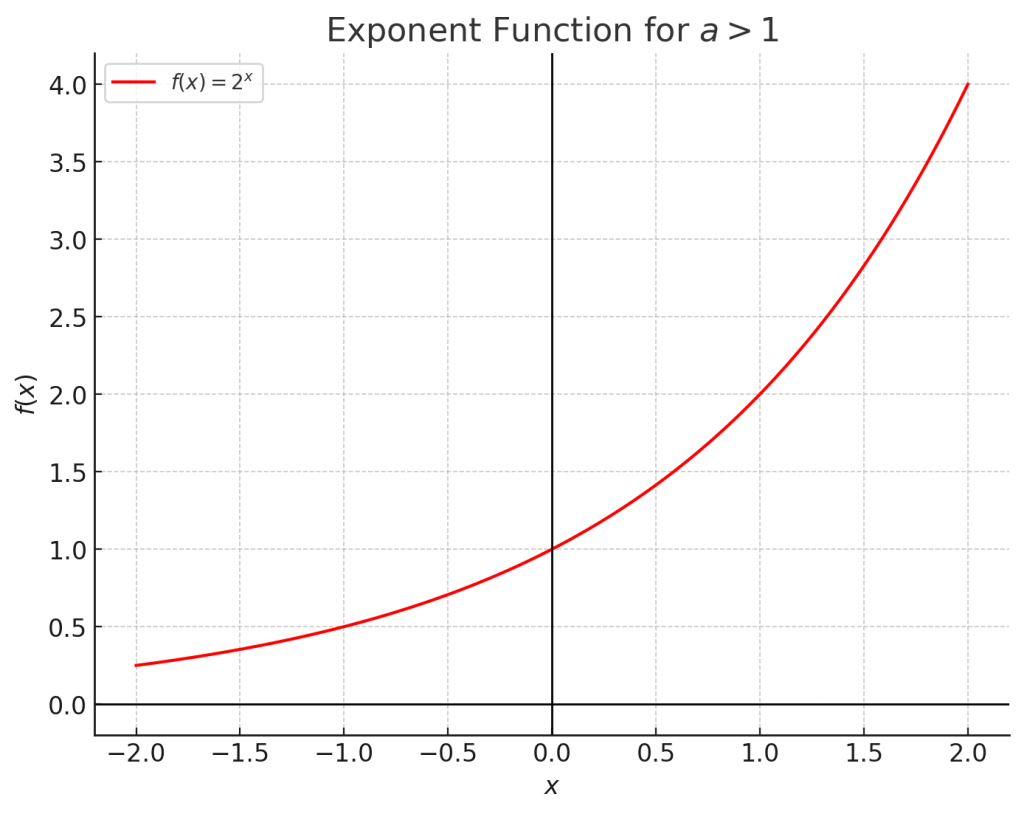
3.1. 例題1：底が1より大きい場合
\[ \log_2 (2x + 3) > 2\log_2 x \]
真数条件より、$2x+3>0,x>0$となるので、$x>0$となる。
与えられた式を変形すると
$$\log_2 (2x + 3) >\log_2 x^2$$
したがって、底が等しいので、真数で比較すると、
\[ \begin{align*} &2x + 3 > x^2 \\ &x^2 – 2x – 3 < 0 \\ &(x – 3)(x + 1) < 0 \end{align*} \]
不等式の範囲は
$$-1<x<3$$
真数条件$x>0$より、
$$0<x<3$$
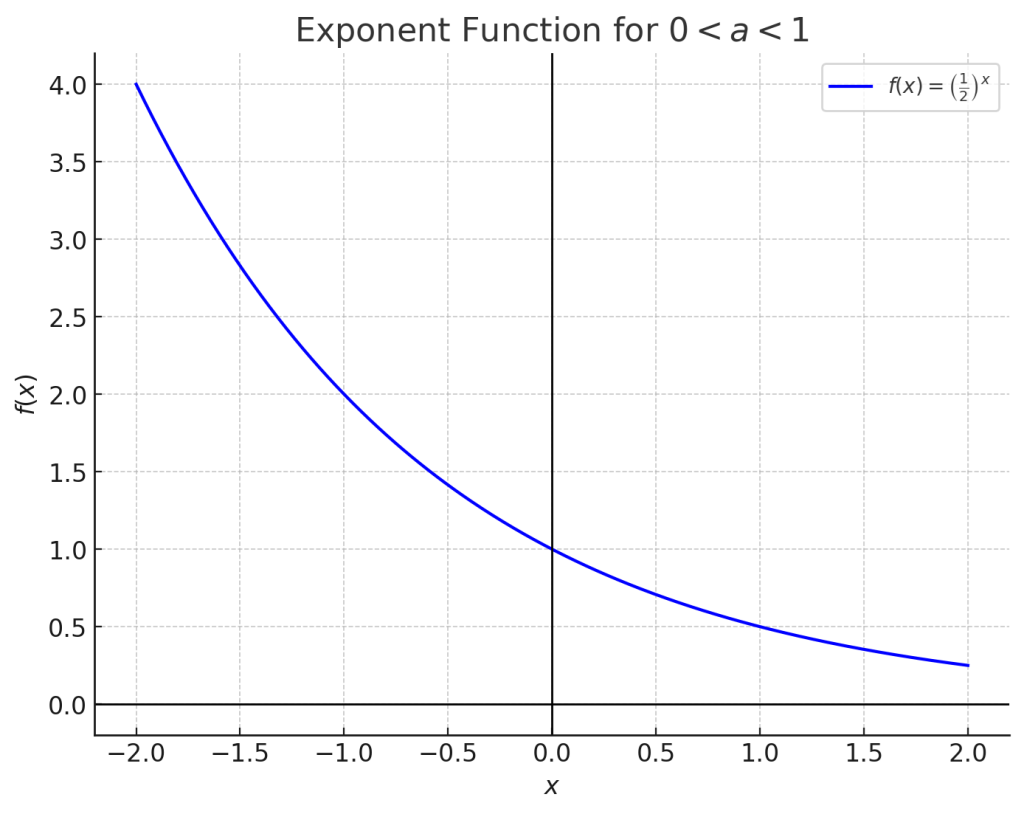
3.2. 例2：底が0より大きく1より小さい場合
\[ \log_{\frac{1}{2}} (x – 1) \leq (\log_{\frac{1}{2}} (x – 1))^2 \]
この不等式を解くためには、まず変数を置き換えて見通しを良くしましょう。
\[ t = \log_{\frac{1}{2}} (x – 1) \]
このとき、不等式は次のようになります。
\[ t \leq t^2 \]
まず、この不等式を整理します。
\[ t^2 – t \geq 0 \]
因数分解すると、
\[ t(t – 1) \geq 0 \]
\(t\) の範囲で、\(t(t – 1) \geq 0\) が成り立つのは \(t \leq 0\) または \(t \geq 1\) です。
次に、元の変数 \(x\) に戻します。
- \(t = \log_{\frac{1}{2}} (x – 1) \leq 0\) のとき\[ \log_{\frac{1}{2}} (x – 1) \leq 0 \]ここで、不等式を満たすためには、\(x – 1 \geq 1\)、すなわち \(x \geq 2\) となります。
- \(t = \log_{\frac{1}{2}} (x – 1) \geq 1\) のとき\[ \log_{\frac{1}{2}} (x – 1) \geq 1 \]不等式を満たすためには、\(x – 1 \leq \frac{1}{2}\)、すなわち \(x \leq \frac{3}{2}\) となります。
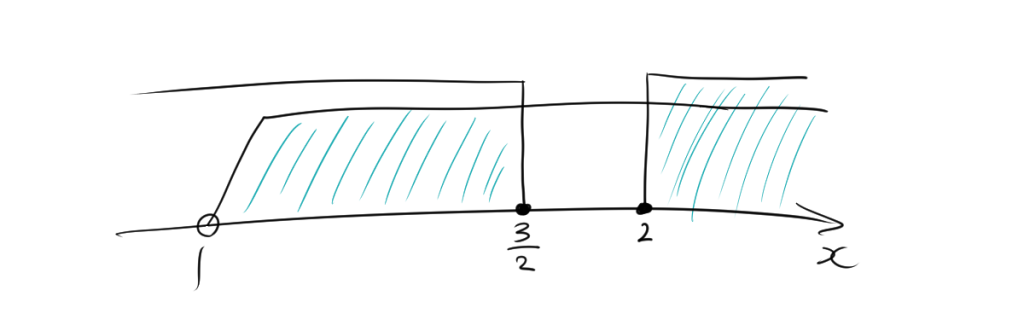
また、真数条件より、$x>1$であるので、
\[ 1 < x \leq \frac{3}{2} かつ x>2\]
