対数関数とは?対数の意味と性質、例題について

1. 対数関数とは
\[ y = \log_a x \]
ここで、\( y=\log_a(x) \) は、「\( a \) を底としてどのような数を乗じれば \( x \) になるのか」を意味します。言い換えると、対数関数は、次の等式に基づきます。
\[ a^y = x \]
xのことを真数と呼び、真数xと底aには条件があります。
- 真数 \( x \) は正の数でなければならない: 対数関数の定義上、真数 \( x \) は常に \( x > 0 \) である必要があります。これは真数条件とも呼ばれます。
- 底 \( a \) も条件付き: 底 \( b \) も \( b > 0 \) かつ \( b \neq 1 \) でなければならず、負の数や 1 では対数が定義されません。
よく使われる底 \( a \) には、次の2つがあります。
- 自然対数(\( \log_e \)): \( e \) はネイピア数(約2.718)で、自然対数は科学や工学でよく使われます。通常、記号としては単に \( \log x \) と表されます。
- 常用対数(\( \log_{10} \)): 底が10の対数で、通常の計算や日常的なスケール(音の強さや地震のマグニチュードなど)で使われます。
2. 対数関数の基本的な性質
2.1. 真数条件
\( y=\log_a(x) \) は、次のように表すことができる。
\[ a^y = x \]
したがって、指数関数$a^y$は常に正であるので、真数$x$も常に正である。
2.2. $\log_a 1$
$1=a^0 $であるので、対数をとると
$$\log _a 1=\log _a a^0 =0$$
2.3. 積の対数
\[ \log_a(x) = p \quad \text{および} \quad \log_a(y) = q \] と置くと、
\[ a^p = x \quad \text{および} \quad a^q = y \]
が成り立ちます。指数法則より、
\[ xy = a^p \cdot a^q = a^{p+q} \]
となります。対数をとると、
\[ \log_a(xy) = \log_a(a^{p+q}) = p + q \]
です。したがって、
\[ \log_a(xy) = \log_a(x) + \log_a(y) \]
2.4. 商の対数
\[ \log_a\left(\frac{x}{y}\right) = \log_a(x) – \log_a(y) \]
\[ \log_a(x) = p \quad \text{および} \quad \log_a(y) = q \]
と置くと、
\[ a^p = x \quad \text{および} \quad a^q = y \]
が成り立ちます。
\[ \frac{x}{y} = \frac{a^p}{a^q} \]
となります。指数法則により、
\[ \frac{a^p}{a^q} = a^{p-q} \]
です。対数をとると
\[ \log_a\left(\frac{x}{y}\right) = \log_a\left(a^{p-q}\right) = p – q \]
です。したがって、
\[ \log_a\left(\frac{x}{y}\right) = \log_a(x) – \log_a(y) \]
2.5. 冪乗(累乗)の対数
\[ \log_a(x) = p \]
と置くと、
\[ a^p = x \]
が成り立ちます。与えられた式の左辺 \(\log_a(x^n)\) を考えます。ここで、\(x^n\) を \(a^p\) で表すと、
\[
x^n = (a^p)^n = a^{pn}
\]
となります。対数をとると、
\[ \log_a(x^n) = \log_a(a^{pn}) = pn \]
です。したがって、
\[ \log_a(x^n) = n \log_a(x) \]
3. 対数関数のグラフ
対数関数は底 \(a\) の値によってグラフの形が異なります。
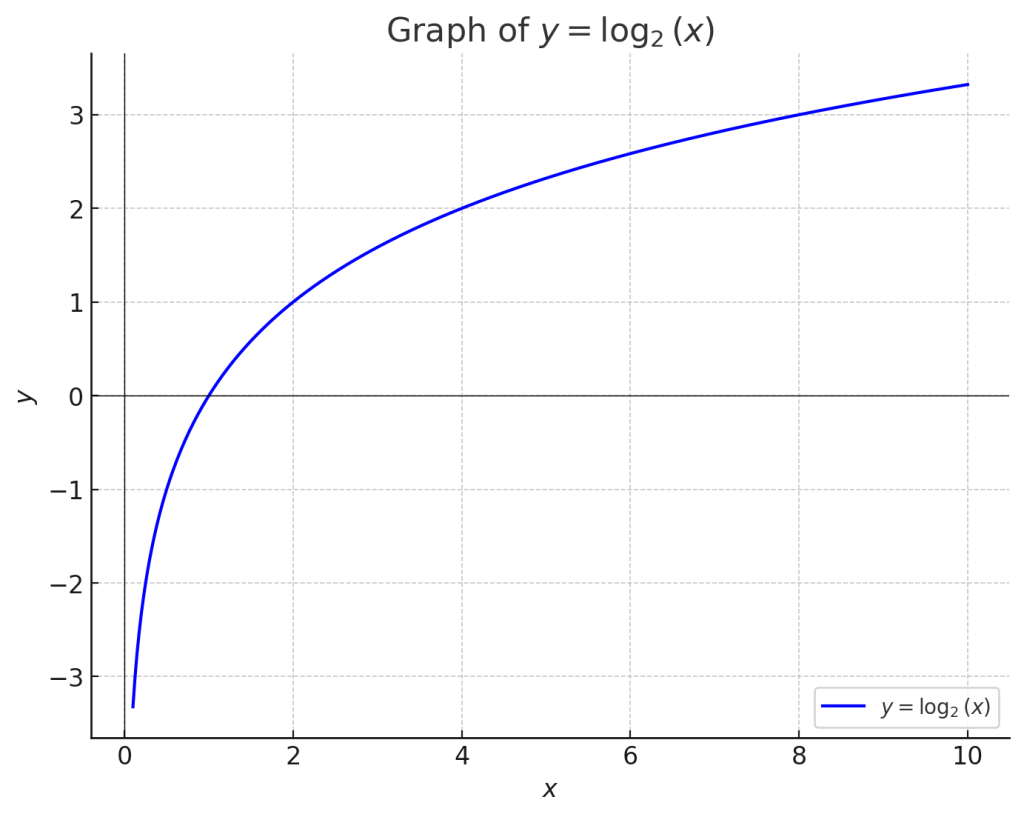
3.1. a>1の場合
底が 2 の対数関数のグラフは、\(x\) が 1 より大きいときに右上がりで増加し、\(0 < x < 1\) の範囲で急激に下がります。
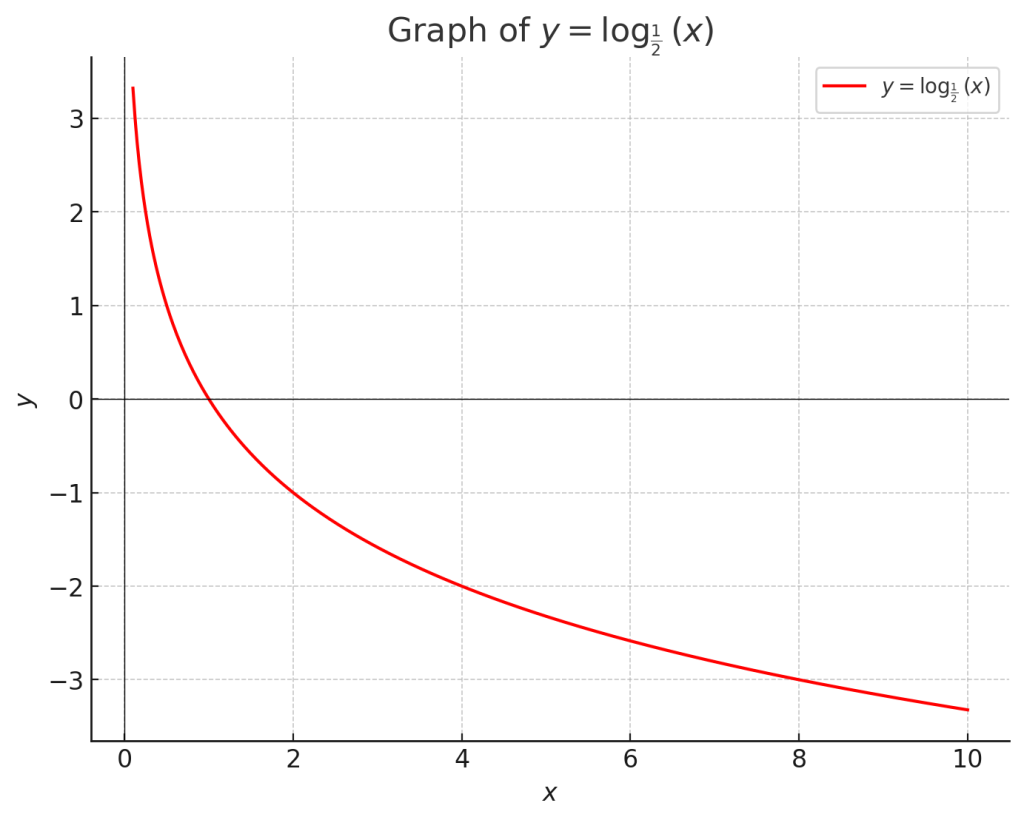
3.2. 0<a<1の場合
底が \( \frac{1}{2} \) の場合、グラフは右下がりとなり、x が増えるにつれて減少します。
3.3. 特徴のまとめ
- 定義域: \(x > 0\) で定義されています。対数関数は正の数にのみ適用できます。
- 増減:
- \(a > 1\) の場合、グラフは右上がり(単調増加)です。たとえば、\(y = \log_2(x)\)。
- \(0 < a < 1\) の場合、グラフは右下がり(単調減少)です。たとえば、\(y = \log_{\frac{1}{2}}(x)\)。
- x 軸との交点: \(x = 1\) のとき、\(y = \log_a(1) = 0\) です。したがって、すべての対数関数は点 \((1, 0)\) を通ります。
4. 対数関数の計算問題
4.1. 問題 1
次の式を計算しなさい。
\[ \log_2 32 \]
\( 32 = 2^5 \) なので
\[ \log_2 32 = 5 \]
4.2. 問題 2
次の式を計算しなさい。
\[ \log_5 25 \]
\( 25 = 5^2 \) なので、
\[ \log_5 25 = 2 \]
4.3. 問題 3
次の式を計算しなさい。
\[ \log_{10} 1000 \]
\( 1000 = 10^3 \) なので、
\[ \log_{10} 1000 = 3 \]
4.4. 問題 4
次の式を計算しなさい。
\[ \log_7 49 + \log_7 7 \]
\[ \log_7 49 + \log_7 7 = \log_7(49\times 7) = 3 \]
4.5. 問題 5
次の式を計算しなさい。
\[ \log_4 64 – \log_4 16 \]
\[ \log_4 64 – \log_4 16 = log_4 \left(\frac{64}{16} \right) =log_4 4= 1 \]
4.6. 問題 6
次の式を計算しなさい。
\[ \log_9 81 + \log_9 27 \]
\[ \log_9 81 + \log_9 27 = 2 + \frac{3}{2} = \frac{7}{2}\]