【論理回路】AND回路とNAND回路・NOR回路による構成について

はるか

AND回路はすべての入力が1でないと出力が1にならない。

ふゅか

入力のどれかが0だと出力も0になるの。だから、全ての条件が揃わないと結果が出ないみたいな感じね！

1. AND回路とは

AND回路（論理積）は、論理演算の一つで、2つ以上の入力がすべて真（1）である場合にのみ出力が真（1）になるゲートです。入力のいずれかが偽（0）であれば、出力は偽（0）になります。

1.1. 真理値表

ANDゲートの2入力の場合の真理値表は以下の通りです。

1.2. 論理関数の表記

ふゅか

論理関数の表記は「Y = A・B」みたいに書く！

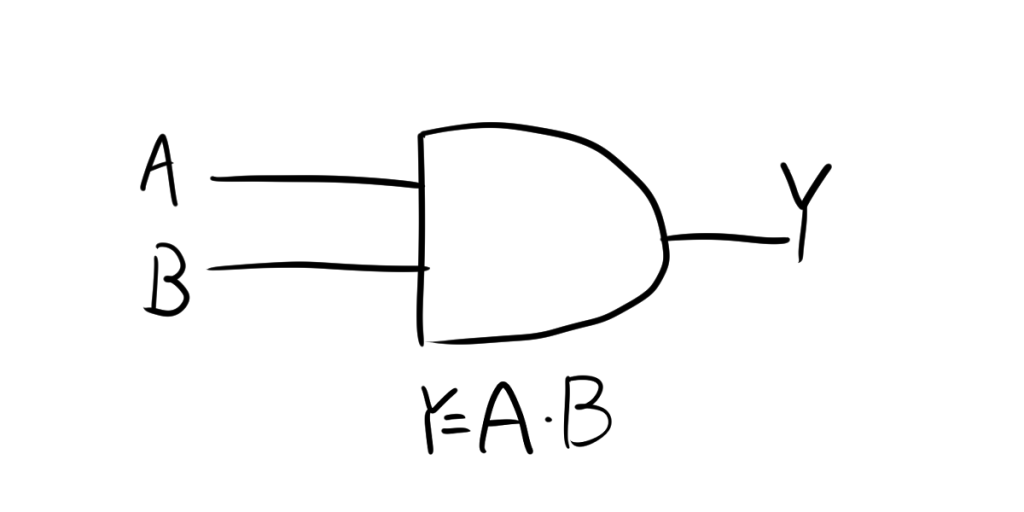
1.3. MIL記号

ANDゲートは、MIL記号で次のように表されます。

1.4. 動作の説明

• 入力Aと入力Bが共に1（真）の場合: 出力は1になります。
• 入力Aまたは入力Bのどちらか、または両方が0（偽）の場合: 出力は0になります。

2. NAND回路でAND回路を表す

ふゅか

そして、AND回路をNAND回路で表す方法もあるのよね！これ、ちょっとトリッキーだけど面白い！

はるか

そうだね。NANDだけで表現できる。

AND回路をNAND回路で表現する方法について、2つのNANDゲートを使った実装手順を説明します。まず、AND回路は以下の式で表されます。

$$Y=A\cdot B$$

しかし、このAND回路をNANDゲートだけで実現するためには、二重否定を利用します。

\[ Y = \overline{\overline{A \cdot B}} \]

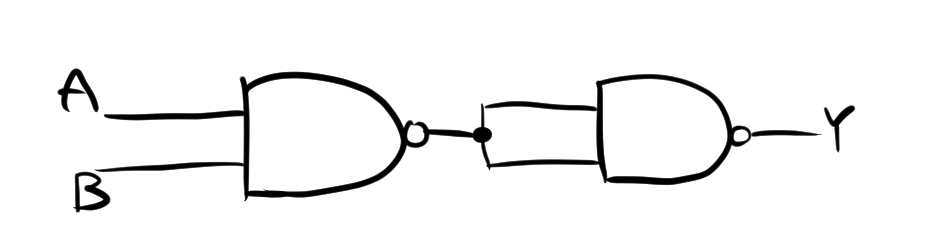
この論理式を回路図にすると、以下のようになります。

このように、NANDゲートを2つ使うことでAND回路を表現することが可能です。NANDゲートはどんな論理回路も実現できるゲートであるため、完全系と呼ばれます。

3. NOR回路でAND回路を表す

ANDゲートの基本的な論理式は以下の通りです。

$$Y = A \cdot B$$

この論理式をNORゲートだけで表現する方法を見ていきましょう。NORゲートは「否定論理和」を実現するゲートであり、出力が1となるのは、すべての入力が0のときだけです。まずは、ANDゲートの論理式を2重否定を使って書き換えます。

$$Y = (\overline{\overline{A}}) \cdot (\overline{\overline{B}})$$

ここで、$A=A+A$、$B=B+B$より、

$$Y=(\overline{ \overline{A+A }})\cdot (\overline {  \overline {B+B}})$$

したがって、

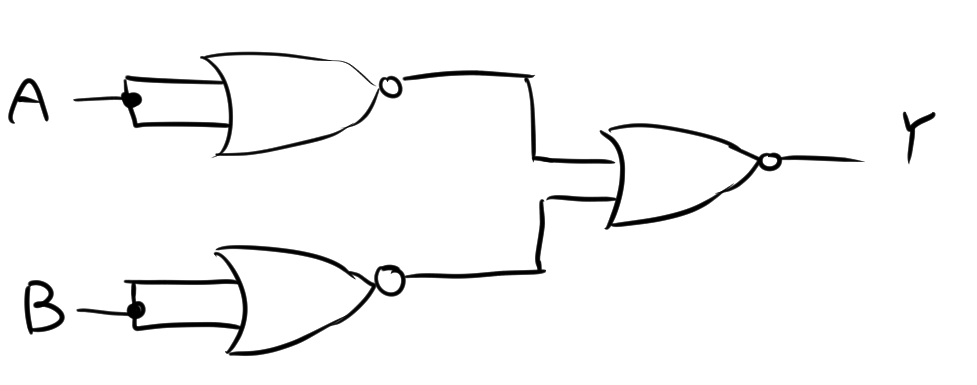
$$Y = \overline{(\overline{A + A}) + (\overline{B + B})}$$

この論式式を図にすると、以下のようになります。