NAND回路と論理式・回路の構成について

1. NAND回路
NAND回路は、デジタル回路の基本的な論理ゲートの一つで、名前の通り「NOT AND」の略です。ANDゲートの出力を否定したものがNANDゲートです。つまり、ANDゲートの出力が1であれば、NANDゲートの出力は0となり、ANDゲートの出力が0であれば、NANDゲートの出力は1となります。
1.1. 真理値表
NANDゲートの真理値表は次の通りです。
| 入力A | 入力B | 出力 (Y) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
1.2. 論理関数の表記
$$Y=\overline{A\cdot B} = \overline A + \overline B$$
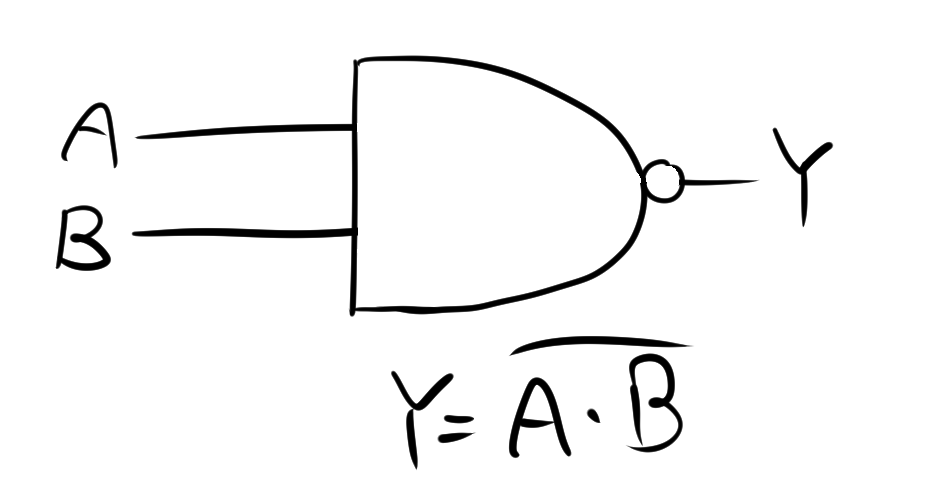
1.3. MIL記号
NANDは、MIL記号で次のように表されます。
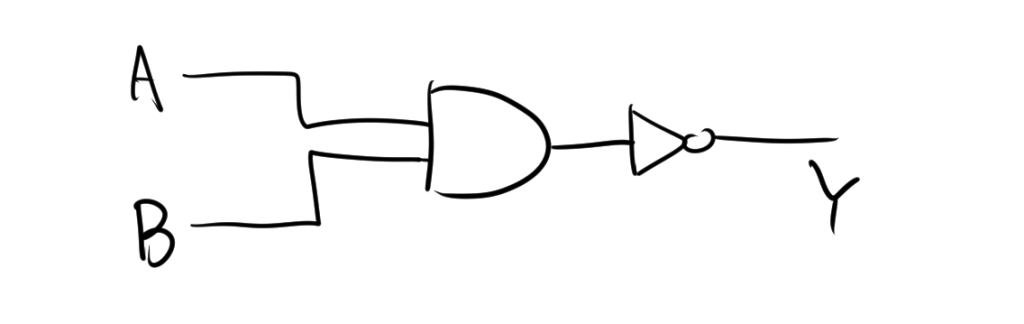
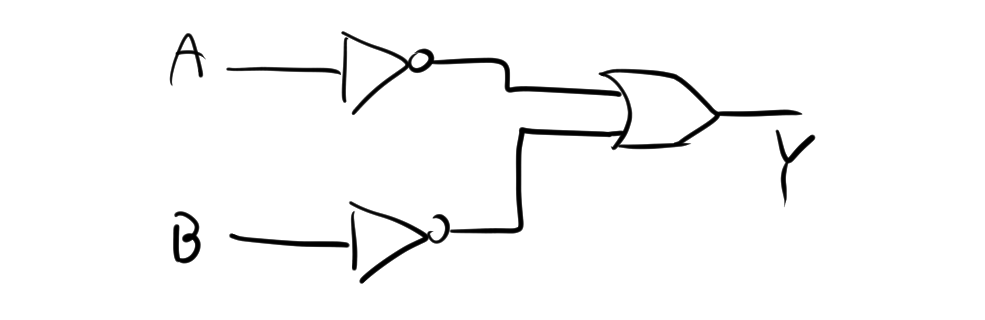
1.4. 回路図
$Y=\overline{A\cdot B} $より、NANDゲートをANDとNOTで構成すると次のような回路になります。
一方で、$Y= \overline A + \overline B$より、NANDゲートをNOTとORで構成すると次のような回路になります。
1.5. NANDゲートの特性
NANDゲートは完全系とも呼ばれ、組み合わせによって他の全ての基本的な論理ゲート(AND、OR、NOT、NOR、XOR、XNOR)を構成することができます。これにより、デジタル回路をNANDゲートだけで構築することも可能です。
2. NANDによる回路の構成
2.1. NOT
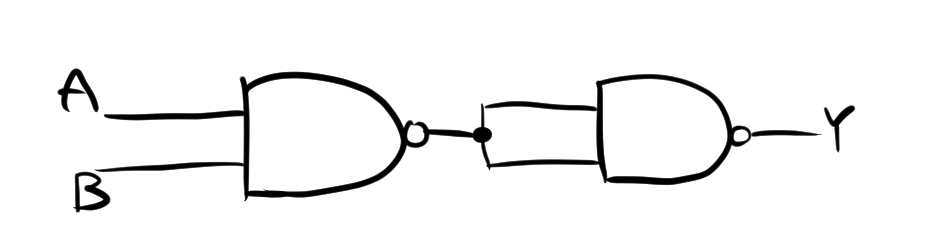
NOTの論理式$Y=\overline{A}$より、
$$Y=\overline {A\cdot A}$$
したがって、回路を書くと次のようになります。
2.2. AND
AND回路は以下の式で表されます。
$$Y=A\cdot B$$
\[ Y = \overline{\overline{A \cdot B}} \]
したがって、回路を書くと次のようになります。
2.3. OR
OR回路の基本的な論理式は次のように表されます。
$$Y = A + B$$
$$Y = (\overline{\overline{A}}) + (\overline{\overline{B}})$$
$$Y = \overline{(\overline{A}) \cdot (\overline{B})}$$
$$Y = \overline{(\overline{A \cdot A}) \cdot (\overline{B \cdot B})}$$
したがって、回路を書くと次のようになります。
2.4. NOR
NOR回路の基本的な論理式は次のように表されます。
$$Y =\overline{ A + B}=\overline A \cdot \overline B = \overline{\overline{\overline A \cdot \overline B}}$$
したがって、回路を書くと次のようになります。
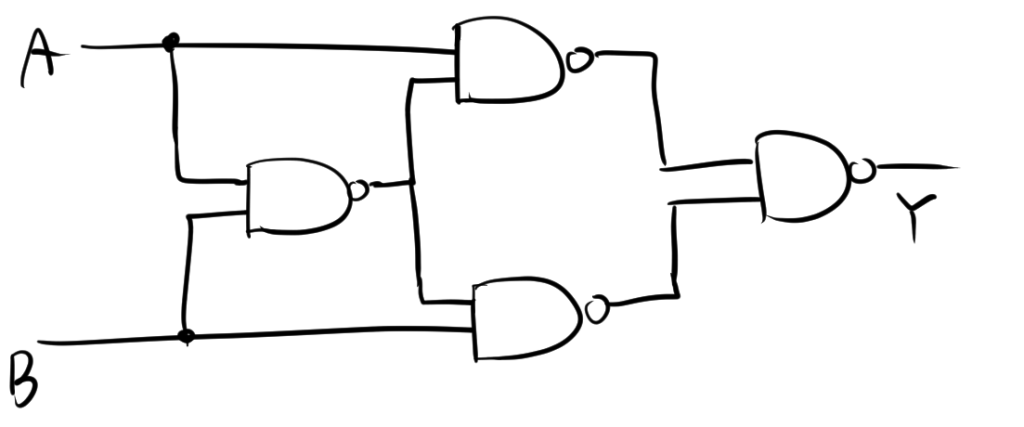
2.5. XOR
XOR回路の基本的な論理式は次のように表されます。
\[ Y = A \cdot \overline{B} + \overline{A} \cdot B \]
\[ =A\cdot\overline A+ A \cdot \overline{B} + \overline{A} \cdot B +B\cdot \overline B \]
\[ = A \cdot (\overline{A} + \overline{B}) + (\overline{A} + \overline{B}) \cdot B \]
\[ = A \cdot \overline {A\cdot B} + B\cdot\overline {A\cdot B} \]
$$=\overline{\overline{A \cdot \overline {A\cdot B} + B\cdot \overline {A\cdot B}}}$$
$$=\overline{\overline{A \cdot \overline {A\cdot B} }\cdot \overline{ B\cdot \overline {A\cdot B}}}$$
したがって、回路を書くと次のようになります。