【論理回路】OR回路とNAND回路・NOR回路による構成について

はるか

OR回路が今回のテーマ。

ふゅか

OR回路は、少なくとも1つの入力が1なら出力が1になるよね♪

1. OR回路とは

OR回路は、論理回路の基本的なゲートの一つで、入力される複数の信号のうち少なくとも一つが”1″（真）であれば、出力を”1″とする回路です。

1.1. ORゲートの基本特性

1.2. 真理値表

2入力のORゲートの真理値表は以下の通りです。

はるか

両方が0のときだけ出力が0。他は全部1になる。

1.3. 論理関数の表記

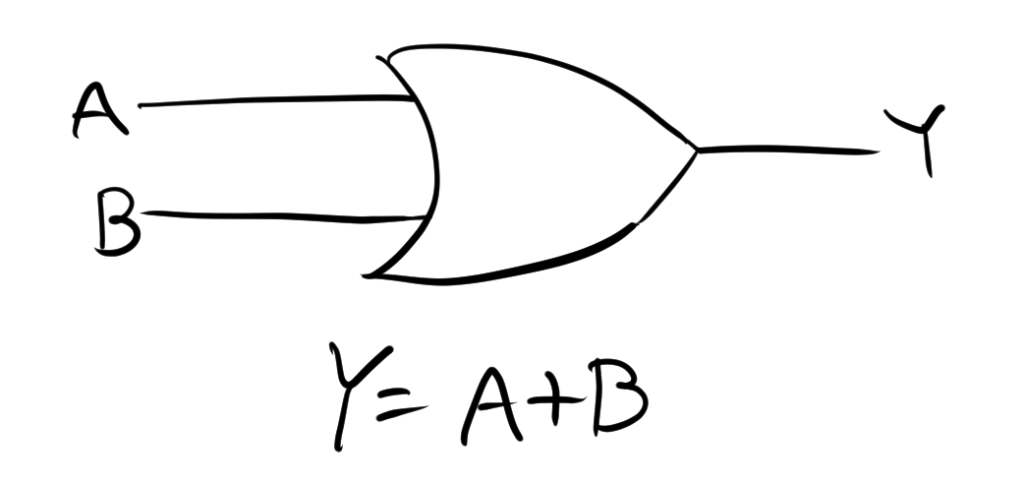
1.4. MIL記号

ORゲートは、MIL記号で次のように表されます。

2. NAND回路による構成

ふゅか

次にNANDゲートを使ってOR回路を構成してみよう！

はるか

二重否定を使う。

NANDゲートを使用してOR回路を構成する方法を説明します。OR回路の基本的な論理式は次のように表されます。

$$Y = A + B$$

ここで、二重否定を利用すると、

$$Y = (\overline{\overline{A}}) + (\overline{\overline{B}})$$

これをさらに簡略化します。

$$Y = \overline{(\overline{A}) \cdot (\overline{B})}$$

ここで、$A=A\cdot A,B=B\cdot B$より、

$$Y = \overline{(\overline{A \cdot A}) \cdot (\overline{B \cdot B})}$$

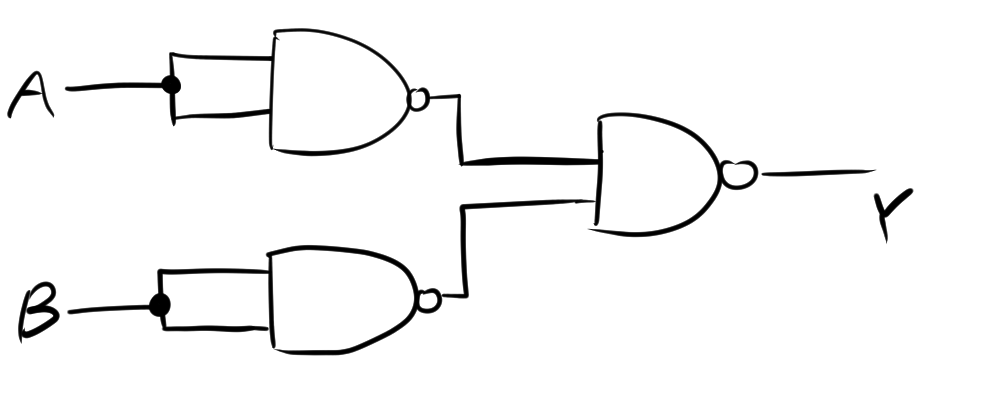
これにより、NANDゲートを使ったOR回路を次の図で確認できます。

3. NOR回路による構成

次に、NORゲートを使用してOR回路を構成する方法を見ていきましょう。OR回路の論理式は次のようになります。

$$Y = A + B$$

二重否定より、

$$Y = \overline{\overline{A + B}}$$

ここで、$\overline{A + B} = \overline{A + B} + \overline{A + B}$より、

$$Y = \overline{(\overline{A + B}) + (\overline{A + B})}$$

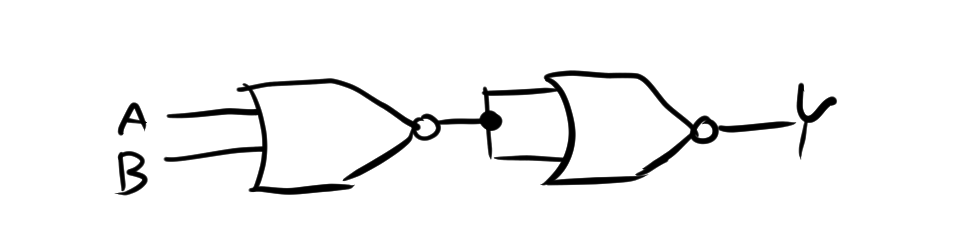
NORゲートだけを使用してOR回路を以下の図で確認することができます。