【論理回路】XOR回路とNAND回路・NOR回路による構成について

1. XOR回路とは
XOR回路は、2つの入力信号に対して出力信号を生成する基本的な論理ゲートの一種です。XOR回路の特性は、2つの入力が異なるときにのみ出力が1になり、同じであるときには出力が0になるというものです。
- XORは排他的論理和と呼ばれる。
- XORはExclusive orの略。
- XOR回路は、加算器の設計で使われます。
1.1. XOR回路の真理値表
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
この真理値表からわかるように、入力Aと入力Bが異なるときだけ出力が1になります。
1.2. XORの論理式
$$Y= A \oplus B=A \cdot\overline B +\overline A \cdot B $$
次に、出力Yの否定である負論理$\overline{Y}$を考えてみます。この場合、次のような論理式が得られます。
$$\overline{Y} =\overline{A}\cdot \overline{B}+ A\cdot B$$
この式は、AとBが同じ場合に出力が0となるANDゲートの否定を表現しています。さらに、この式を否定することで元のXORゲートの論理式に戻すことができます。
$$Y = \overline{\overline{A}\cdot \overline{B} + A\cdot B}$$
1.3. MIL記号
XORは、MIL記号で次のように表されます。
1.4. 回路図
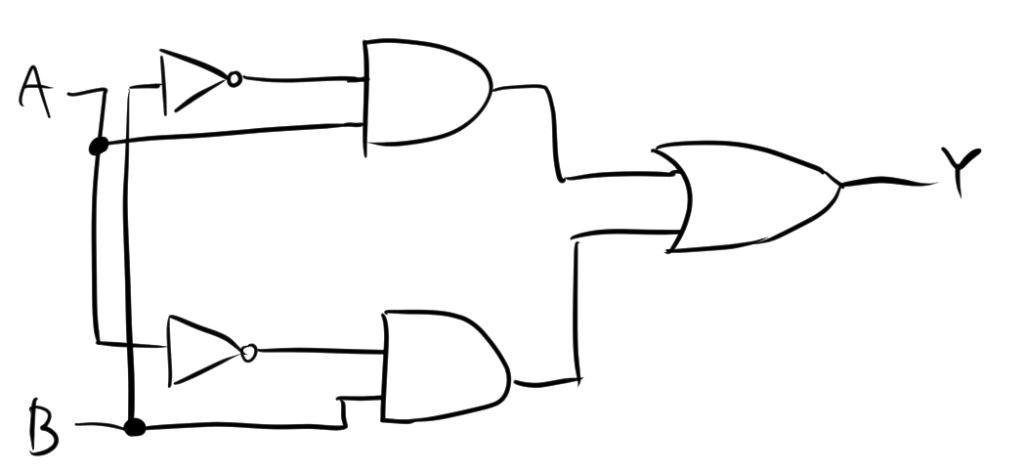
$Y= A \cdot\overline{B} +\overline A \cdot B $より、XORゲートをNOT回路とAND回路、OR回路で表すと次のようになります。
この場合、使用している素子の数は5個になります。
一方で、$Y = \overline{\overline{A}\cdot \overline{B} + A\cdot B}$より、NOT回路とAND回路、OR回路を利用して論理回路を構成すると次のようになります。
2. NANDによる構成
まず、以下の論理式について考えます。
\[ Y = A \cdot \overline{B} + \overline{A} \cdot B \]
この式は、AとBのXORを表しています。次に、この式を二重否定してみましょう。
\[ Y = \overline{\overline{A \cdot \overline{B} + \overline{A} \cdot B}} \]
二重否定の法則により、この式は元の式と同じであることがわかります。ただし、否定の位置を変えることで異なる回路構成を考えることができます。
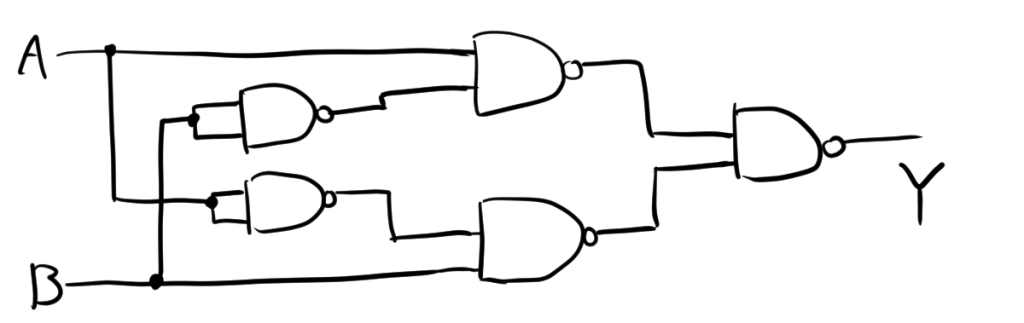
\[ Y = \overline{\overline{A \cdot \overline{B}} \cdot \overline{\overline{A} \cdot B}} \]
回路図を書くと次のようになります。
2.1. 素子を減らす
\[ Y = A \cdot \overline{B} + \overline{A} \cdot B \]
\[ =A\cdot\overline A+ A \cdot \overline{B} + \overline{A} \cdot B +B\cdot \overline B \]
\[ = A \cdot (\overline{A} + \overline{B}) + (\overline{A} + \overline{B}) \cdot B \]
\[ = A \cdot \overline {A\cdot B} + B\cdot\overline {A\cdot B} \]
二重否定をすると、
$$=\overline{\overline{A \cdot \overline {A\cdot B} + B\cdot \overline {A\cdot B}}}$$
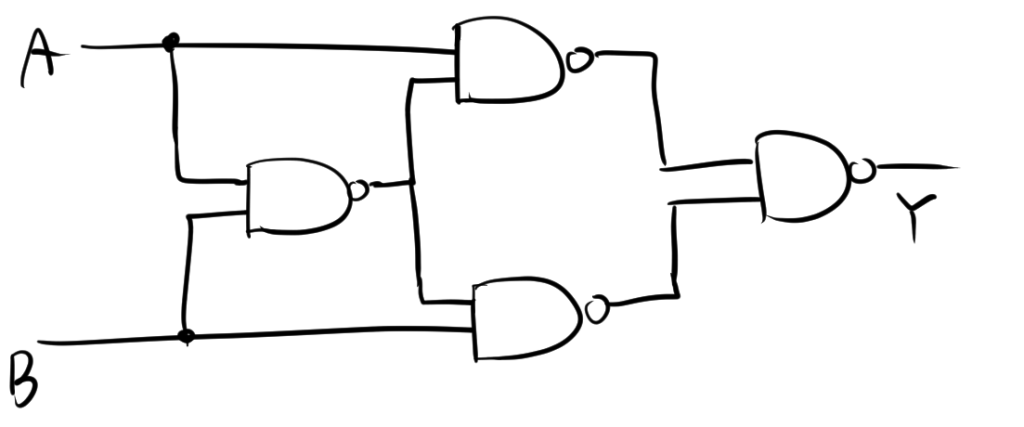
$$=\overline{\overline{A \cdot \overline {A\cdot B} }\cdot \overline{ B\cdot \overline {A\cdot B}}}$$
この回路の構成を回路図で表すと、以下のようにNANDゲートを4つに減らすことができます。
3. NORによる構成
まず、XORの出力Yは次のようになります。
\[ Y = \overline{\overline{A \cdot B} + A\cdot B} \]
$\overline{A + B} = \overline{A \cdot B} $より、次のように変形します。
\[ Y = \overline{\overline{A + B} + A\cdot B} \]
さらに、ABの部分も二重否定をすると次のようになります。
\[ Y = \overline{\overline{A + B} + \overline{\overline{A\cdot B}}} \]
\[ Y = \overline{\overline{A + B} + \overline{\overline{A} + \overline{B}}} \]
$A=A+A,B=B+B$より、
\[ Y = \overline{\overline{A + B} + \overline{\overline{A+A} + \overline{B+B}}} \]
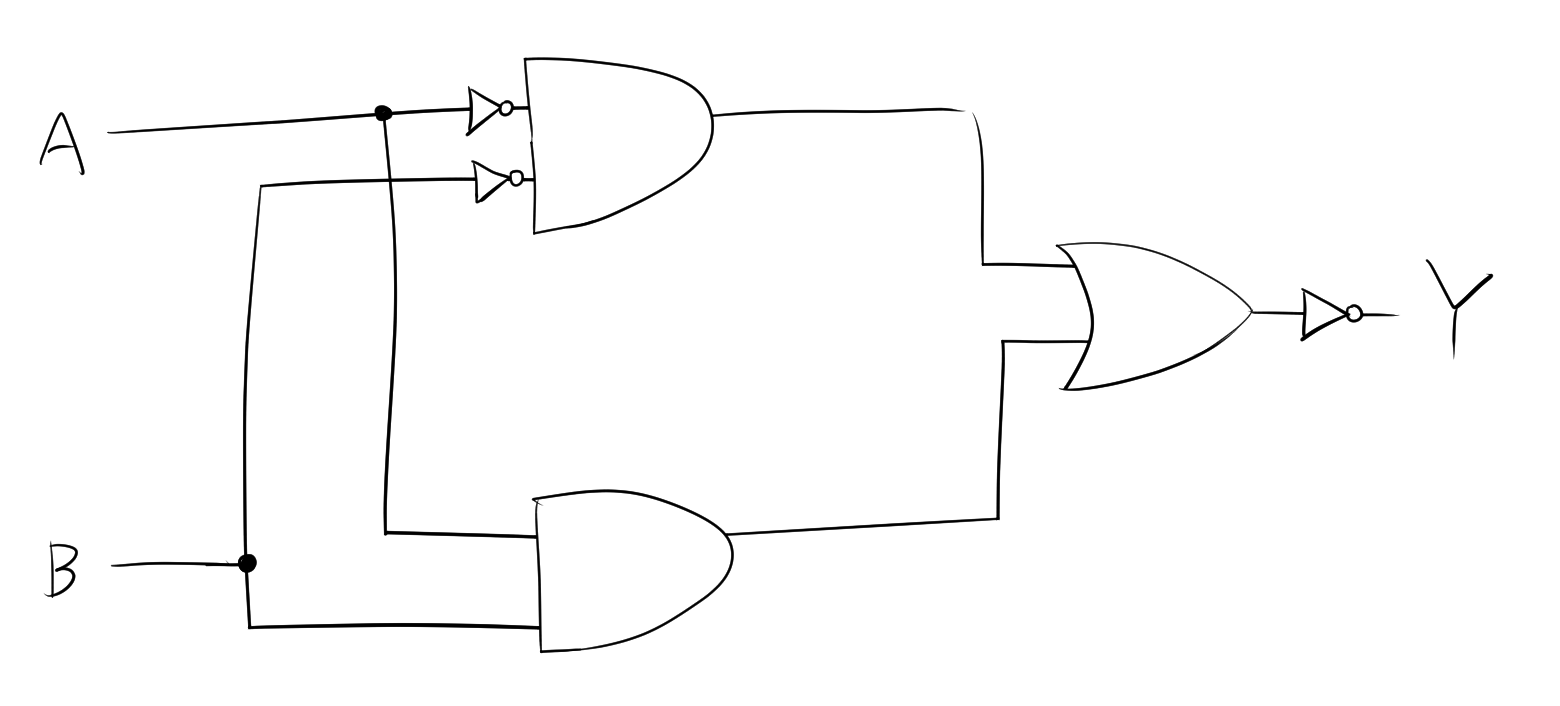
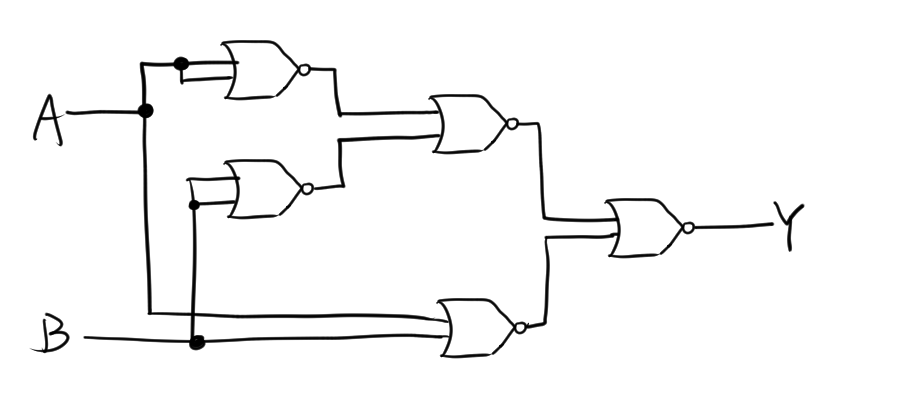
この論理式に基づいて回路図を描くと、次のようになります。