【図解】数学的帰納法とそのパターン、イメージ、例題について

1. 数学的帰納法

数学的帰納法は、数列や数式、命題が「すべての自然数」に対して成り立つことを証明するための強力な方法です。この方法は、自然数 \( n \) に対して一般的な性質が成立するかどうかを証明する際に使われ、特に数列の性質や公式の証明によく登場します。

1.1. 数学的帰納法の基本パターン

1.2. 数学的帰納法の直感的なイメージ

ドミノ倒しで数学的帰納法を考えてみましょう。ドミノは大量に並んでいるとします。仮に、n=1（一番左端にある）のドミノが倒れるとします。

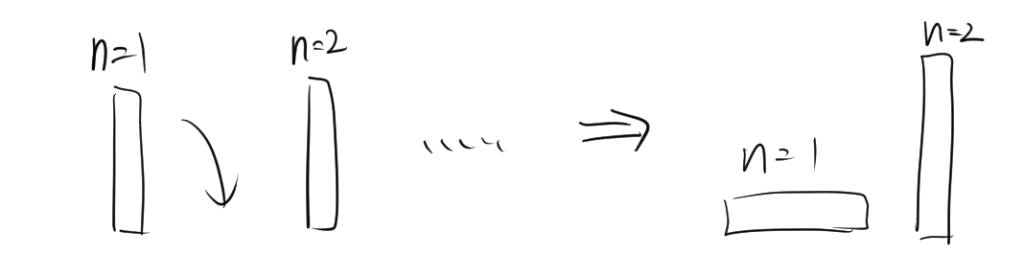図のように、n=1のドミノが倒れたとしても、n=2は倒れません。もしかしたら、倒れるかもしれませんが、必ずすべてのドミノが倒れるとは限りません。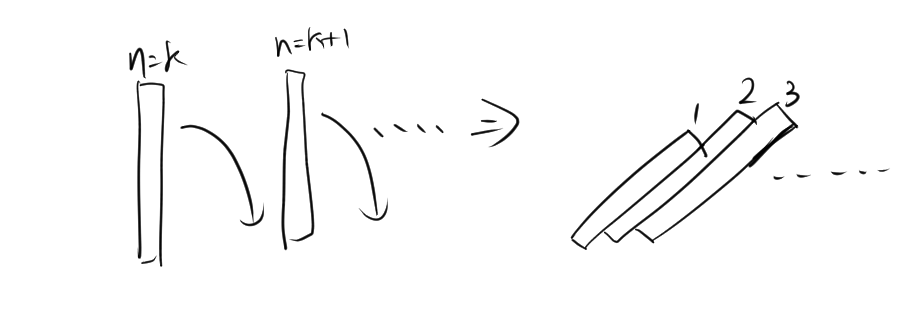では、仮にあるkが倒れるときに、k+1が倒れるとすると、n=1（一番左端にある）のドミノが倒れるので、n=2のドミノが倒れます。同様に、

• n=2のドミノが倒れると、n=3のドミノが倒れる
• n=3のドミノが倒れると、n=4のドミノが倒れる

これがずっと続くため、すべてのドミノが倒れるということが言えます。この考え方が、数学的帰納法の基本的なイメージです。

1.3. 具体例

ここで、例を使って数学的帰納法を見てみましょう。

\( n = 1 \) の場合、左辺は \( 1 \) で、右辺は \( \frac{1(1+1)}{2} = 1 \) です。よって、命題は成り立ちます。

\( n = k \) のときに命題が成り立つと仮定します。つまり、

\[ 1 + 2 + 3 + \dots + k = \frac{k(k+1)}{2} \]

この仮定を使って、\( n = k+1 \) の場合に命題が成り立つことを示します。左辺に \( k+1 \) を加えると、

\[ 1 + 2 + 3 + \dots + k + (k+1) = \frac{k(k+1)}{2} + (k+1) \]

これを整理すると、

\[ = \frac{k(k+1)}{2} + \frac{2(k+1)}{2} = \frac{(k+1)(k+2)}{2} \]

となり、右辺が \( \frac{(k+1)(k+2)}{2} \) であることが示されました。つまり、\( n = k+1 \) の場合にも命題が成り立つことが証明されました。したがって、数学的帰納法により、この数式はすべての自然数 \( n \) に対して成り立つことが示されました。

2. 数学的帰納法の例題

2.1. 例題1:平方和

まず、\( n = 1 \) の場合を確認します。

左辺： \[ 1^2 = 1 \]

右辺： \[ \frac{1(1+1)(2 \times 1 + 1)}{6} = \frac{1 \times 2 \times 3}{6} = 1 \]

よって、\( n = 1 \) の場合、等式は成り立っています。

$n= k $に対して、次の等式が成り立つと仮定します。

\[ 1^2 + 2^2 + 3^2 + \cdots + k^2 = \frac{k(k+1)(2k+1)}{6} \]

\( n = k+1 \) の場合、仮定より、

\[ 1^2 + 2^2 + \cdots + k^2 + (k+1)^2 = \frac{k(k+1)(2k+1)}{6} + (k+1)^2 \]

次に、右辺を共通因数 \( (k+1) \) でまとめます。

\[ = \frac{k(k+1)(2k+1)}{6} + \frac{6(k+1)^2}{6} \]

\[ = \frac{(k+1)\left(k(2k+1) + 6(k+1)\right)}{6} \]

これを展開すると、

\[ = \frac{(k+1)(2k^2 + k + 6k + 6)}{6} = \frac{(k+1)(2k^2 + 7k + 6)}{6} \]

これは次のように因数分解できます。

\[ \begin{align*}&= \frac{(k+1)(k+2)(2k+3)}{6} \\ &= \frac{(k+1)\{(k+1)+1\}\{2(k+1)+1\}}{6} \end{align*}\]

よって、\( n = k+1 \) の場合でも等式が成り立つことが示されました。

数学的帰納法により次の等式が成り立つことが証明されました。

\[ 1^2 + 2^2 + 3^2 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6} \]

2.2. 例題2：不等式

\( f(n) \) を次のように定義します。

\[ f(n) = 2^n – n^2 \]

まず、\( n = 5 \) の場合の不等式を確認します。

\[ 2^5 = 32, \quad 5^2 = 25 \]

したがって、$f(5)$は

$$f(5)=32-25=7\geq 0$$

よって、 \( n = 5 \) では不等式が成り立っています。

次に、ある \( n = k \) に対して、次の仮定が成り立つとします。

\[ f(k) = 2^k – k^2 > 0 \]

次に、\( n = k + 1 \) のとき、まず、\( f(k+1) \) を計算します。

\[\begin{align*} f(k+1) &= 2^{k+1} – (k+1)^2 \\ &= 2 \cdot 2^k – (k^2 + 2k + 1) \\ &= 2 \cdot 2^k – 2k^2 + k^2-2k-1 \\ &= 2( \cdot 2^k – k^2 )+ k^2-2k-1 \\ &= 2f(k)+ k^2-2k-1 \end{align*} \]

仮定より、 \( f(k) = 2^k – k^2 > 0 \)

\[\begin{align*} f(k+1)  &= 2f(k)+ k^2-2k-1 \\ &> k^2-2k-1 \\ &= (k-1)^2-2 \end{align*} \]

したがって、平方完成の形から二次関数を評価すると次のような図になる。

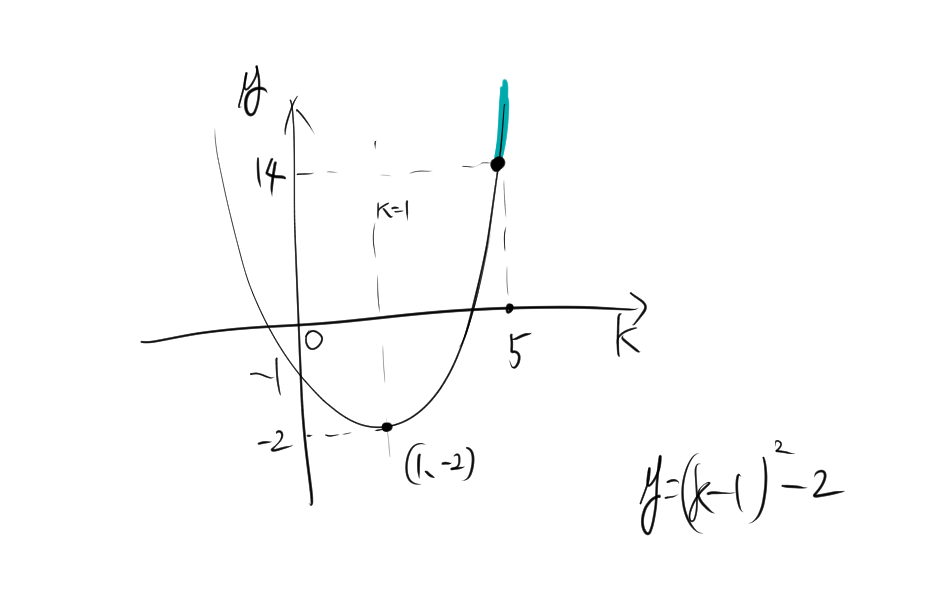$k\geq 5$であるので、青色の範囲の部分になるため、$ (k-1)^2-2$の最小値はk=5のときであるので、

\[\begin{align*} f(k+1)  &>(k-1)^2-2 \\ &\geq 4^2-2 =14>0 \end{align*} \]

\( f(k+1) > 0 \) が成り立つことが示されました。$n=k+1$の場合においても成り立つ。したがって、数学的帰納法により、 \( n \geq 5 \) のすべての場合において、

\[\begin{align*} f(n)&>0 \end{align*}\]

が成り立つことが証明されました。したがって、

\[\begin{align*} & 2^n – n^2 >0\\ &\therefore  2^n > n^2 \end{align*}\]

2.3. 例題3：指数関数の余り

まず、\( n = 1 \) の場合を確認します。

\[ 7^1 – 2^1 = 7 – 2 = 5 \]

よって、5で割り切れます。

\( n=k \) に対して、次の仮定が成り立つとします。

\[ 7^k – 2^k \text{ は 5 で割り切れる} \]

つまり、

\[ 7^k – 2^k = 5m \quad \text{(ある整数 \( m \) が存在する)} \]

次に \( n = k+1 \) の場合、

\[ \begin{align*}7^{k+1} – 2^{k+1} &= 7 \cdot 7^k – 2 \cdot 2^k \\ &= 7(7^k – 2^k) + (7 \cdot 2^k – 2 \cdot 2^k) \\ &= 7(7^k – 2^k) + (5 \cdot 2^k) \end{align*}\]

ここで、より \( 7^k – 2^k = 5m \) なので、

\[ = 7 \cdot 5m + 5 \cdot 2^k = 5(7m + 2^k) \]

よって、\( 7^{k+1} – 2^{k+1} \) は 5 で割り切れることが示されました。$n=k+1$の場合においても成り立つ。数学的帰納法により、任意の自然数 \( n \) に対して、

\[ 7^n – 2^n \text{ は 5 で割り切れる} \]

が成り立つことが証明されました。

捕捉になりますが、この問題は合同式を利用すると簡単に解くことができます。

$7^n \equiv 2^n \pmod 5$より、

$$7^n-5^n \equiv 2^n-2^n \equiv 0\pmod 5$$

このことから、5で割り切れます。

3. 数学的帰納法のバリエーション

数学的帰納法には、いくつかのバリエーションがあります。

3.1. 二つの項を仮定

まず、n=1とn=2の場合が成り立つことを確認します。次に、n=kとn=k+1の場合が成り立つと仮定します。そして、その仮定に基づいてn=k+2の場合にも成り立つことを証明します。

3.2. n<kが成り立つと仮定

通常の数学的帰納法では \( n = k \) の場合を仮定しますが、\( n = 1, 2, \dots, k \) のすべての場合が成り立つことを仮定します。このあと、n=k+1が成り立つことを示します。

3.3. 不等式のパターン

不等式を数学的帰納法で証明する際のポイントは、まず差を考え、それを用いて不等号を示す方法です。具体的には、次のような不等式が与えられたとしましょう。

$$g(n) > h(n)$$

このとき、両辺の差 \( f_n = g(n) – h(n) \) を定義します。数学的帰納法における一般的な流れとして、まず \( n = 1 \) のときに \( f_1 > 0 \) が成り立つことを確認します。次に、ある \( n = k \) のときに \( f_k > 0 \) が成り立つと仮定し、この仮定のもとで \( f_{k+1} > 0 \) が成立することを示します。

差をとらなくても証明はできますが、私はこのやり方が好きです。

3.4. 無限降下法

通常の数学的帰納法では、\( n = 1 \) から \( n = k \) へと進むのに対し、無限降下法では、大きい値から小さい値へと証明を行います。