MDPの定義・具体例・状態価値関数・方策・練習問題について

1. MDPとは
MDPはMarkov Decision Processの略です。マルコフ決定過程と呼ばれます。
1.1. MDPの定義
- 状態 (State, \(S\)): エージェントが現在いる環境の状況を表します。
- 行動 (Action, \(A\)): エージェントが取ることができる選択肢や行動を表します。
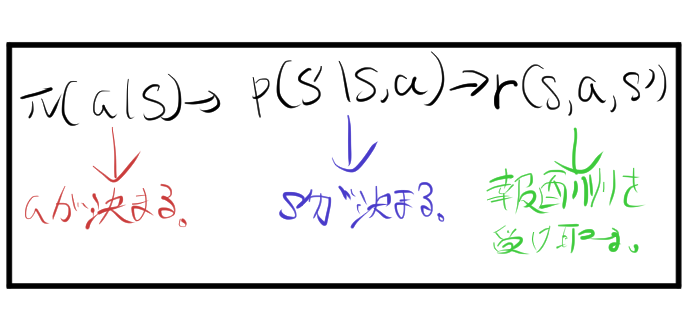
- 遷移確率 (Transition Probability, \(P(s’ | s, a)\)): ある状態 \(s\) で行動 \(a\) を取ったときに、次の状態 \(s’\) に遷移する確率を示します。これがマルコフ性の特徴で、次の状態は現在の状態と行動のみに依存します。
- 報酬 (Reward, \(R\)): 状態 \(s\) で行動 \(a\) を取り$s’$に遷移したとき、得られる報酬を表します。報酬関数を用いて計算される。
MDPの遷移は次のような時系列データとなります。ここで \( t \) は時刻を表します。
\[ S_0, A_0, R_1,S_1, A_1, R_2, S_2, A_2, \dots \]
- \( S_t \): 時刻 \( t \) での状態
- \( A_t \): 時刻 \( t \) で選択された行動
- \( R_{t} \): 時刻 \( t \) で得られた報酬
エージェントと環境の関係を図にすると、次のようになります。
1.2. マルコフ性
マルコフ性とは、確率過程において、現在の状態が次の状態に影響を与えるのに、過去の状態が直接的な役割を果たさないという性質を指します。
\[ P(s_{t+1} | s_t, s_{t-1}, \dots, s_0) = P(s_{t+1} | s_t) \]
この式は、次の状態 \( s_{t+1} \) が現在の状態 \( s_t \) のみに依存し、それ以前の状態 \( s_{t-1}, s_{t-2}, \dots \) には依存しないことを意味します。
MDPにおいて、各状態での決定がマルコフ性に従います。つまり、将来の状態や報酬に影響を与えるのは現在の状態と現在の行動だけで、過去の状態や行動は影響しません。
1.3. 報酬関数
報酬関数 \( R(s, a, s’) \) とは、マルコフ決定過程 (MDP: Markov Decision Process) における報酬の定義方法の一つで、特定の状態 \( s \) で特定の行動 \( a \) を取った後、次の状態 \( s’ \) に遷移したときに得られる報酬を表しています。
具体的な例を用いると、次のようになります。
- \( R(s_0, a_0, s_0) = 2 \): 状態 \( s_0 \) で行動 \( a_0 \) を取り、その結果も再び状態 \( s_0 \) に戻ったときにエージェントは報酬として 2 を受け取ります。
- \( R(s_1, a_1, s_0) = 4 \): 状態 \( s_1 \) で行動 \( a_1 \) を取り、次の状態が \( s_0 \) に遷移した場合、報酬として 4 が得られます。
2. エージェントの方策について
方策とは、エージェントが各状態でどの行動を選択するかを決定するルールまたは戦略のことです。方策には主に2種類があります。確率的方策と決定論的方策です。基本的に確率的方策が使用されます。
2.1. 確率的方策
確率的方策では、エージェントがある状態 \( s \) にいるときに、各行動 \( a \) を特定の確率で選択します。この方策は、状態と行動のペアに対する確率分布として表されます。つまり、状態 \( s \) における行動 \( a \) をとる条件付き確率を \( \pi(a|s) \) として表します。
例えば、ある状態 \( s \) で、エージェントが行動 \( a_1 \) を取る確率が 0.7、行動 \( a_2 \) を取る確率が 0.3 である場合、方策は次のように表されます。
\[ \pi(a_1|s) = 0.7, \quad \pi(a_2|s) = 0.3 \]
方策 \( \pi \) に関して表にすると次のようになる。
| 状態 \( s \) | 行動 \( a_1 \) | 行動 \( a_2 \) |
|---|---|---|
| \( s \) | 0.7 | 0.3 |
2.2. 決定論的方策
決定論的方策では、エージェントがある状態 \( s \) にいるときに、常に同じ行動 \( a \) を選択します。つまり、この方策では、状態 \( s \) が与えられたときに、エージェントの行動が一意に決まります。この場合、方策は関数として表されます。
\[ \pi(s) = a \]
例えば、ある状態 \( s \) で、エージェントが常に行動 \( a_1 \) を選択する場合、方策は次のように表されます。
\[ \pi(s) = a_1 \]
3. 状態価値関数
3.1. 収益とは
\[ G_t = \sum_{k=0}^{\infty} \gamma^k R_{t+k} \]
ここで、
- \( G_t \) は、時刻 \( t \) での収益(累積報酬)です。
- \( R_{t+k} \) は、時刻 \( t+k \) に得られる報酬です。
- \( \gamma \) は割引率(0から1の間の値)で、将来の報酬に対する重みを表します。
3.2. 状態価値関数とは
$$v_{\pi}(s)=\mathbb{E}[G_t|S_t=s,\pi]$$
また、次のように書かれることもある。
$$v_{\pi}(s)=\mathbb{E}_{\pi}[G_t|S_t=s]$$
4. MDPの目標
マルコフ決定過程(MDP)において、エージェントの目標は、ある方策 \( \pi \) に従って行動を選択し、累積報酬(収益)を最大化することです。つまり、収益を最大化する方策を見つけるということです。
4.1. 最適な方策の発見
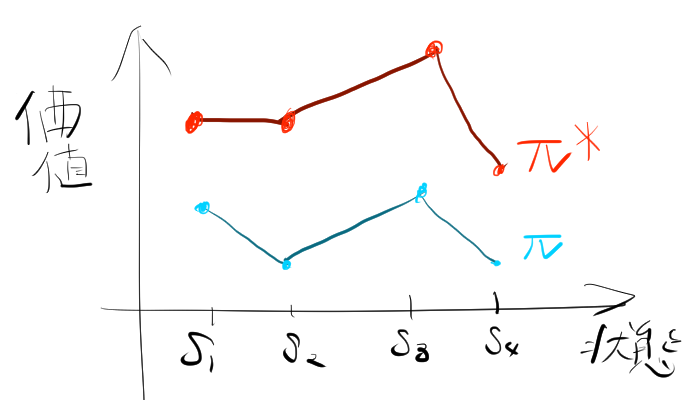
エージェントは、すべての状態 \( s \) に対して、最も高い価値をもたらす方策 \( \pi^* \) を見つけることを目指します。最適な方策 \( \pi^* \) は、すべての可能な方策の中で、状態価値関数 \( v_{\pi}(s) \) が最大となる方策です。これを次のように表します。
\[ \pi^* = \arg\max_{\pi} v_{\pi}(s) \]
この最適方策により、エージェントはどの状態にいても、可能な限り最高の累積報酬を得ることができます。
5. 練習問題
5.1. 練習問題1: 確率的方策に関連する問題
- 状態 \( s_0 \) で行動 \( a_0 \) を取る確率は \( \pi(a_0|s_0) = 0.4 \)
- 状態 \( s_0 \) で行動 \( a_1 \) を取る確率は \( \pi(a_1|s_0) = 0.6 \)
- 状態 \( s_1 \) で行動 \( a_0 \) を取る確率は \( \pi(a_0|s_1) = 0.7 \)
- 状態 \( s_1 \) で行動 \( a_1 \) を取る確率は \( \pi(a_1|s_1) = 0.3 \)
- 状態 \( s_0 \) において、エージェントが行動 \( a_0 \) を連続して2回取る確率を求めなさい。
- 状態 \( s_1 \) において、エージェントが行動 \( a_1 \) を1回取った後、状態 \( s_0 \) に遷移し、次に行動 \( a_1 \) を取る確率を求めなさい。
マルコフ性に注意して計算する。
状態 \( s_0 \) において、エージェントが行動 \( a_0 \) を連続して2回取る確率状態 \( s_0 \) において、エージェントが行動 \( a_0 \) を取る確率は \( \pi(a_0|s_0) = 0.4 \) です。したがって、2回連続で行動 \( a_0 \) を取る確率は次のように計算されます。\[ \text{確率} = \pi(a_0|s_0) \times \pi(a_0|s_0) = 0.4 \times 0.4 = 0.16 \]
状態 \( s_1 \) において、エージェントが行動 \( a_1 \) を1回取った後、状態 \( s_0 \) に遷移し、次に行動 \( a_1 \) を取る確率まず、状態 \( s_1 \) において行動 \( a_1 \) を取る確率は \( \pi(a_1|s_1) = 0.3 \) です。その後、状態 \( s_0 \) に遷移し、次に行動 \( a_1 \) を取る確率は \( \pi(a_1|s_0) = 0.6 \) です。したがって、全体の確率は次のように計算されます。\( a_1 \)0
5.2. 練習問題2: 決定論的方策と状態価値関数
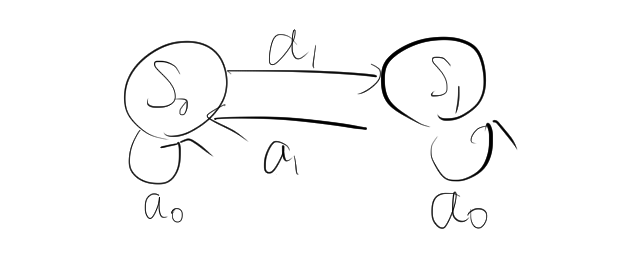
- \( f(s_0, a_0) = s_0 \)
- \( f(s_1, a_0) = s_1 \)
- \( f(s_0, a_1) = s_1 \)
- \( f(s_1, a_1) = s_0 \)
ここで、状態 \( s_0 \) と \( s_1 \) が存在し、エージェントは行動 \( a_0 \) または \( a_1 \) を選択できます。報酬 \( R(s, a) \) は次のように与えられます。
- \( R(s_0, a_0,s_0) = 2 \)
- \( R(s_0, a_1,s_1) = 3 \)
- \( R(s_1, a_0,s_1) = 1 \)
- \( R(s_1, a_1,s_0) = 4 \)
エージェントが次の方策に従う場合、8通りの状態価値関数 \( v_{\pi}(s) \) を求めなさい。
- 方策 \( \pi_1 \): 状態 \( s_0 \) では常に \( a_0 \) を選択し、状態 \( s_1 \) では常に \( a_0 \) を選択する。
- 方策 \( \pi_2 \): 状態 \( s_0 \) では常に \( a_1 \) を選択し、状態 \( s_1 \) では常に \( a_1 \) を選択する。
- 方策 \( \pi_3 \): 状態 \( s_0 \) では常に \( a_0 \) を選択し、状態 \( s_1 \) では常に \( a_1 \) を選択する。
- 方策 \( \pi_4 \): 状態 \( s_0 \) では常に \( a_1 \) を選択し、状態 \( s_1 \) では常に \( a_0 \) を選択する。
割引率は \( \gamma = 0.9 \) とします。
各方策に従って、状態価値関数 \( v_{\pi}(s) \) を計算します。決定論的方策であるため、収益は確率的にふるまわない。したがって、収益を直接計算することで、状態価値関数を計算することができる。
5.2.1. 方策 \( \pi_1 \)
状態 \( s_0 \) では常に \( a_0 \) を選択し、状態 \( s_1 \) では常に \( a_0 \) を選択する。
| 状態 \( s \) | 行動 \( a \) | 次の状態 \( s’ \) | 報酬 \( R(s, a, s’) \) |
|---|---|---|---|
| \( s_0 \) | \( a_0 \) | \( s_0 \) | 2 |
| \( s_1 \) | \( a_0 \) | \( s_1 \) | 1 |
1. 状態 \( s_0 \) の場合:
\[ G_t = R(s_0, a_0,s_0) + \gamma \cdot R(s_0, a_0,s_0) + \gamma^2 \cdot R(s_0, a_0,s_0) + \dots \] \[ G_t = 2 + 0.9 \times 2 + 0.9^2 \times 2 + \dots \]
この無限等比級数を計算します。初項が 2、等比率が \( 0.9 \) です。
\[ G_t = \frac{2}{1 – 0.9} = \frac{2}{0.1} = 20 \]
したがって、
\[ v_{\pi_1}(s_0) = 20 \]
2. 状態 \( s_1 \) の場合:
\[ G_t = R(s_1, a_0,s_1) + \gamma \cdot R(s_1, a_0,s_1) + \gamma^2 \cdot R(s_1, a_0,s_1) + \dots \] \[ G_t = 1 + 0.9 \times 1 + 0.9^2 \times 1 + \dots \]
同様に、初項が 1、等比率が \( 0.9 \) です。
\[ G_t = \frac{1}{1 – 0.9} = \frac{1}{0.1} = 10 \]
したがって、
\[ v_{\pi_1}(s_1) = 10 \]
5.2.2. 方策 \( \pi_2 \)
状態 \( s_0 \) では常に \( a_1 \) を選択し、状態 \( s_1 \) では常に \( a_1 \) を選択する。
| 状態 \( s \) | 行動 \( a \) | 次の状態 \( s’ \) | 報酬 \( R(s, a, s’) \) |
|---|---|---|---|
| \( s_0 \) | \( a_1 \) | \( s_1 \) | 3 |
| \( s_1 \) | \( a_1 \) | \( s_0 \) | 4 |
1. 状態 \( s_0 \) の場合:
\[ G_t = R(s_0, a_1,s_1) + \gamma \cdot R(s_1, a_1,s_0) + \gamma^2 \cdot R(s_0, a_1,s_1) + \dots \]
状態 \( s_0 \) で行動 \( a_1 \) を選択すると、次に状態 \( s_1 \) へ遷移し、その後また行動 \( a_1 \) を選択すると、再び状態 \( s_0 \) に戻ります。これを考慮すると、次のように計算できます。
\[ G_t = 3 + 0.9 \times 4 + 0.9^2 \times 3 + 0.9^3 \times 4 + \dots \]
この級数を2つの無限等比級数に分けて計算します。
まず、奇数項の和を計算すると、
\[ G_t^{(1)} = 3 + 0.9^2 \times 3 + 0.9^4 \times 3 + \dots = 3 \times \frac{1}{1 – 0.9^2} = \frac{3}{1 – 0.81} = \frac{3}{0.19} \approx 15.79 \]
次に、偶数項の和を計算すると、
\[ G_t^{(2)} = 0.9 \times 4 + 0.9^3 \times 4 + 0.9^5 \times 4 + \dots = 4 \times \frac{0.9}{1 – 0.9^2} = 4 \times \frac{0.9}{0.19} \approx 18.95 \]
したがって、全体の和は、
\[ G_t = G_t^{(1)} + G_t^{(2)} \approx 15.79 + 18.95 \approx 34.74 \]
したがって、
\[ v_{\pi_2}(s_0) \approx 34.74 \]
2. 状態 \( s_1 \) の場合:
\[ G_t = R(s_1, a_1) + \gamma \cdot R(s_0, a_1) + \gamma^2 \cdot R(s_1, a_1) + \dots \]
状態 \( s_1 \) で行動 \( a_1 \) を選択すると、次に状態 \( s_0 \) へ遷移し、その後また行動 \( a_1 \) を選択すると、再び状態 \( s_1 \) に戻ります。これを考慮すると、次のように計算できます。
\[ G_t = 4 + 0.9 \times 3 + 0.9^2 \times 4 + 0.9^3 \times 3 + \dots \]
この無限級数を2つの無限等比級数に分けて計算します。
まず、偶数項の和を計算すると、
\[ G_t^{(2)} = 4 + 0.9^2 \times 4 + 0.9^4 \times 4 + \dots = 4 \times \frac{1}{1 – 0.9^2} \approx 21.05 \]
次に、奇数項の和を計算すると、
\[ G_t^{(1)} = 0.9 \times 3 + 0.9^3 \times 3 + 0.9^5 \times 3 + \dots = 3 \times \frac{0.9}{1 – 0.9^2} \approx 14.21 \]
したがって、全体の和は、
\[ G_t = G_t^{(2)} + G_t^{(1)} \approx 21.05 + 14.21 \approx 35.26 \]
したがって、
\[ v_{\pi_2}(s_1) \approx 35.26 \]
5.2.3. 方策 \( \pi_3 \)
状態 \( s_0 \) では常に \( a_0 \) を選択し、状態 \( s_1 \) では常に \( a_1 \) を選択する。
| 状態 \( s \) | 行動 \( a \) | 次の状態 \( s’ \) | 報酬 \( R(s, a, s’) \) |
|---|---|---|---|
| \( s_0 \) | \( a_0 \) | \( s_0 \) | 2 |
| \( s_1 \) | \( a_1 \) | \( s_0 \) | 4 |
1. 状態 \( s_0 \) の場合:
\[ G_t = R(s_0, a_0,s_0) + \gamma \cdot R(s_1, a_1,s_0) + \gamma^2 \cdot R(s_0, a_0,s_0) + \dots \]
状態 \( s_0 \) で行動 \( a_0 \) を選択すると、次に状態 \( s_0 \) に留まり、そこから状態 \( s_1 \) へ遷移し、その後再び \( s_0 \) へ遷移します。したがって、次のように計算します。
\[ G_t = 2 + 0.9 \times 4 + 0.9^2 \times 2 + 0.9^3 \times 4 + \dots \]
まず、奇数項の和を計算すると、
\[ G_t^{(1)} = 2 + 0.9^2 \times 2 + 0.9^4 \times 2 + \dots = 2 \times \frac{1}{1 – 0.9^2} \approx 10.53 \]
次に、偶数項の和を計算すると、
\[ G_t^{(2)} = 0.9 \times 4 + 0.9^3 \times 4 + 0.9^5 \times 4 + \dots = 4 \times \frac{0.9}{1 – 0.9^2} \approx 18.95 \]
したがって、全体の和は、
\[ G_t = G_t^{(1)} + G_t^{(2)} \approx 10.53 + 18.95 \approx 29.48 \]
したがって、
\[ v_{\pi_3}(s_0) \approx 29.48 \]
2. 状態 \( s_1 \) の場合:
\[ G_t = R(s_1, a_1) + \gamma \cdot R(s_0, a_0) + \gamma^2 \cdot R(s_1, a_1) + \dots \]
状態 \( s_1 \) で行動 \( a_1 \) を選択すると、次に状態 \( s_0 \) へ遷移し、その後再び状態 \( s_1 \) へ遷移します。これを
考慮して次のように計算します。
\[ G_t = 4 + 0.9 \times 2 + 0.9^2 \times 4 + 0.9^3 \times 2 + \dots \]
まず、偶数項の和を計算すると、
\[ G_t^{(2)} = 4 + 0.9^2 \times 4 + 0.9^4 \times 4 + \dots = 4 \times \frac{1}{1 – 0.9^2} \approx 21.05 \]
次に、奇数項の和を計算すると、
\[ G_t^{(1)} = 0.9 \times 2 + 0.9^3 \times 2 + 0.9^5 \times 2 + \dots = 2 \times \frac{0.9}{1 – 0.9^2} \approx 9.48 \]
したがって、全体の和は、
\[ G_t = G_t^{(2)} + G_t^{(1)} \approx 21.05 + 9.48 \approx 30.53 \]
したがって、
\[ v_{\pi_3}(s_1) \approx 30.53 \]
5.2.4. 方策 \( \pi_4 \)
状態 \( s_0 \) では常に \( a_1 \) を選択し、状態 \( s_1 \) では常に \( a_0 \) を選択する。
| 状態 \( s \) | 行動 \( a \) | 次の状態 \( s’ \) | 報酬 \( R(s, a, s’) \) |
|---|---|---|---|
| \( s_0 \) | \( a_1 \) | \( s_1 \) | 3 |
| \( s_1 \) | \( a_0 \) | \( s_1 \) | 1 |
1. 状態 \( s_0 \) の場合:
\[ G_t = R(s_0, a_1,s_1) + \gamma \cdot R(s_1, a_0,s_1) + \gamma^2 \cdot R(s_0, a_1,s_1) + \dots \]
状態 \( s_0 \) で行動 \( a_1 \) を選択すると、次に状態 \( s_1 \) へ遷移し、その後状態 \( s_0 \) へ戻ります。これを考慮すると、次のように計算できます。
\[ G_t = 3 + 0.9 \times 1 + 0.9^2 \times 3 + 0.9^3 \times 1 + \dots \]
まず、奇数項の和を計算すると、
\[ G_t^{(1)} = 3 + 0.9^2 \times 3 + 0.9^4 \times 3 + \dots = 3 \times \frac{1}{1 – 0.9^2} \approx 15.79 \]
次に、偶数項の和を計算すると、
\[ G_t^{(2)} = 0.9 \times 1 + 0.9^3 \times 1 + 0.9^5 \times 1 + \dots = 1 \times \frac{0.9}{1 – 0.9^2} \approx 4.74 \]
したがって、全体の和は、
\[ G_t = G_t^{(1)} + G_t^{(2)} \approx 15.79 + 4.74 \approx 20.53 \]
そのため、正しい結果は
\[ v_{\pi_4}(s_0) \approx 20.53 \]
2. 状態 \( s_1 \) の場合:
\[ G_t = R(s_1, a_0,s_1) + \gamma \cdot R(s_1, a_0,s_1) + \gamma^2 \cdot R(s_1, a_0,s_1) + \dots \] \[ G_t = 1 + 0.9 \times 1 + 0.9^2 \times 1 + \dots \]
この無限等比級数を計算します。初項が 1、等比率が \( 0.9 \) です。
\[ G_t = \frac{1}{1 – 0.9} = \frac{1}{0.1} = 10 \]
したがって、
\[ v_{\pi_4}(s_1) = 10 \]
方策ごとの状態価値関数をまとめると次のようになります。
- 方策 \( \pi_1 \)
- \( v_{\pi_1}(s_0) = 20 \)
- \( v_{\pi_1}(s_1) = 10 \)
- 方策 \( \pi_2 \)
- \( v_{\pi_2}(s_0) \approx 34.74 \)
- \( v_{\pi_2}(s_1) \approx 35.26 \)
- 方策 \( \pi_3 \)
- \( v_{\pi_3}(s_0) \approx 29.48 \)
- \( v_{\pi_3}(s_1) \approx 30.53 \)
- 方策 \( \pi_4 \)
- \( v_{\pi_4}(s_0) \approx 20.53 \)
- \( v_{\pi_4}(s_1) = 10 \)




.png.webp)