平均値の定理の証明、イメージと具体例について

はるか

平均値の定理は、関数が区間内で連続で微分可能なら、その区間内に平均変化率と接線の傾きが一致する点が存在する。

ふゅか

そうそう！例えば、関数 \( f(x) = x^2 \) で区間 \([1, 3]\) を考えると、その中で瞬間の変化率が平均変化率と一致する点が見つかるのよ！

1. 平均値の定理

平均値の定理は、ある関数がある区間で連続かつその内部で微分可能である場合、その区間のどこかに関数の平均変化率とその瞬間の変化率が一致する点が存在することを示しています。

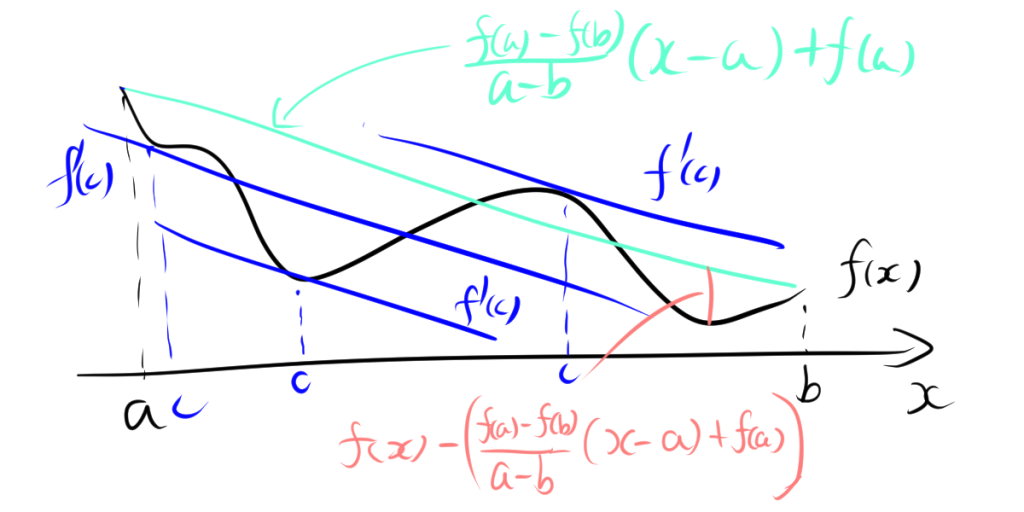
1.1. 直感的なイメージ

平均値の定理の直感的な意味は、曲線 \( y = f(x) \) 上の2点 \((a, f(a))\) と \((b, f(b))\) を結ぶ直線の傾きが、曲線上のどこかでその瞬間の接線の傾きに一致するということです。

1.2. 具体例

例えば、関数 \( f(x) = x^2 \) を区間 \([1, 3]\) で考えます。この関数は連続で、すべての実数において微分可能です。平均値の定理を適用すると、次のようになります。

1. \( f(1) = 1^2 = 1 \)
2. \( f(3) = 3^2 = 9 \)
3. 平均変化率は \(\frac{f(3) – f(1)}{3 – 1} = \frac{9 – 1}{2} = 4\)

したがって、区間 \((1, 3)\) のどこかに、\( f'(c) = 2c \) が 4 になるような点 \( c \) が存在します。この場合、\( 2c = 4 \) ですから、\( c = 2 \) となります。したがって、\( c = 2 \) で接線の傾きと平均変化率が一致します。

2. 証明

平均値の定理の証明は、ロルの定理を利用して行います。

2.1. ロルの定理

はるか

ロルの定理は、ある関数が閉区間で連続で開区間で微分可能で、両端の値が同じなら、その間に微分係数がゼロになる点があるってこと。

ふゅか

ロルの定理を使って、平均値の定理の証明を行うの。新しい関数 \( g(x) \) を定義して、$g(x)$がロルの定理を満たすか調べるわ！

2.2. 平均値の定理の証明

関数 \( f(x) \) が閉区間 \([a, b]\) で連続であり、開区間 \((a, b)\) で微分可能であるとします。まず、新しい関数 \( g(x) \) を次のように定義します。

\[g(x) = f(x) – \frac{f(b) – f(a)}{b – a} \cdot (x – a)\]

この関数 \( g(x) \) の性質を調べてみましょう。

関数 \( f(x) \) は \([a, b]\) で連続で、\((a, b)\) で微分可能なので、\( g(x) \) も同様に \([a, b]\) で連続で、\((a, b)\) で微分可能です。

\( g(a) \) と \( g(b) \) を計算します。

\[g(a) = f(a) – \frac{f(b) – f(a)}{b – a} \cdot (a – a) = f(a)\]

\[g(b) = f(b) – \frac{f(b) – f(a)}{b – a} \cdot (b – a) = f(b) – (f(b) – f(a)) = f(a)\]

よって、\( g(a) = g(b) \) です。

ロルの定理により、\( g'(x) = 0 \) となる点 \( c \) （\( a < c < b \)）が存在します。

\( g'(x) \) を求めると、

\[g'(x) = f'(x) – \frac{f(b) – f(a)}{b – a}\]

これが 0 になる点 \( c \) が存在するので、

\[f'(c) – \frac{f(b) – f(a)}{b – a} = 0\]

したがって、

\[f'(c) = \frac{f(b) – f(a)}{b – a}\]

これで、平均値の定理の証明が完了しました。