マージソート
1. マージソートの動作のイメージ図
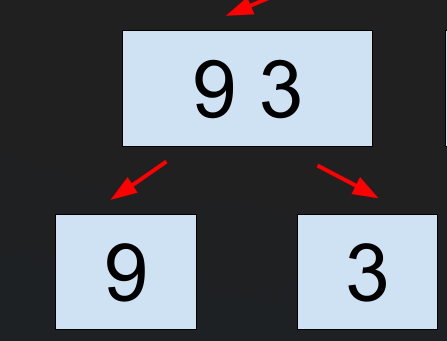
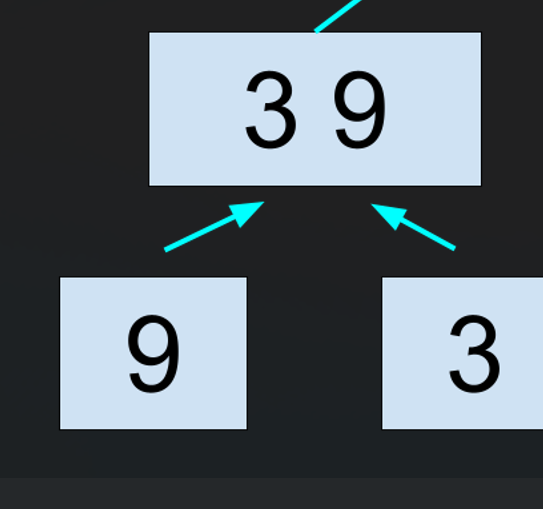
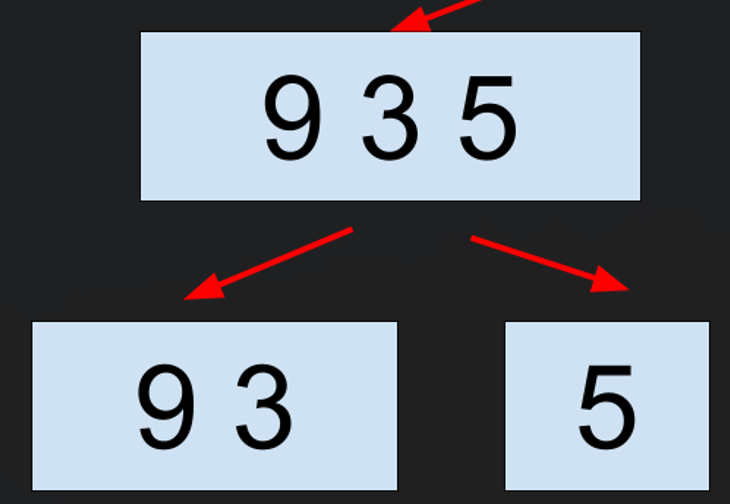
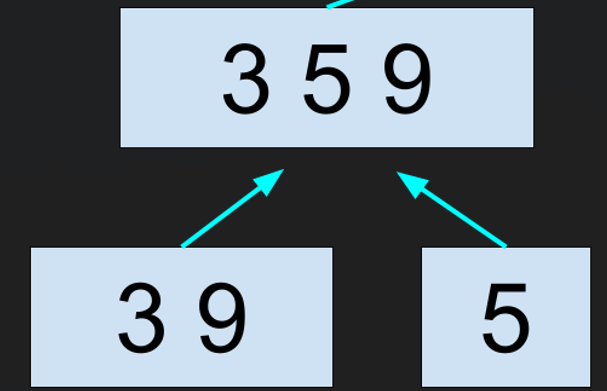
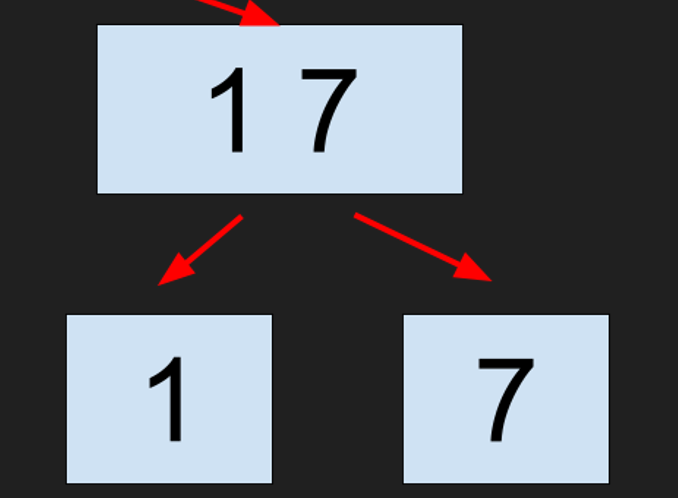
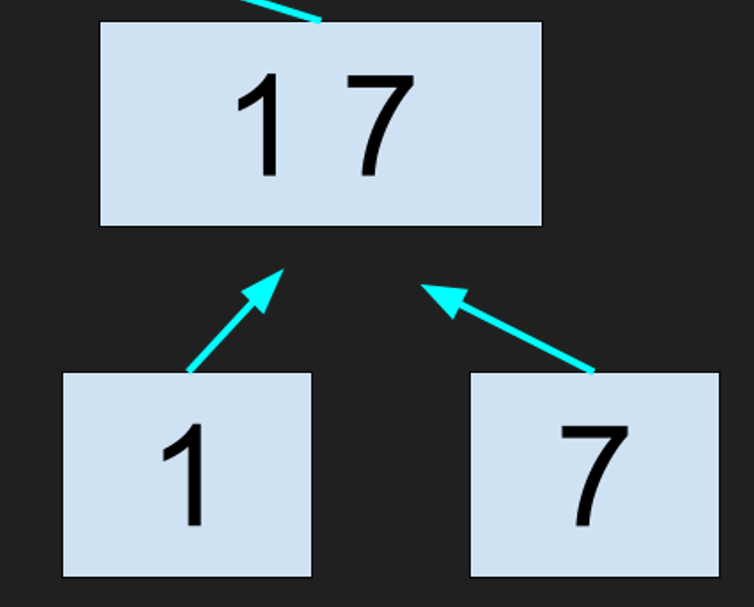
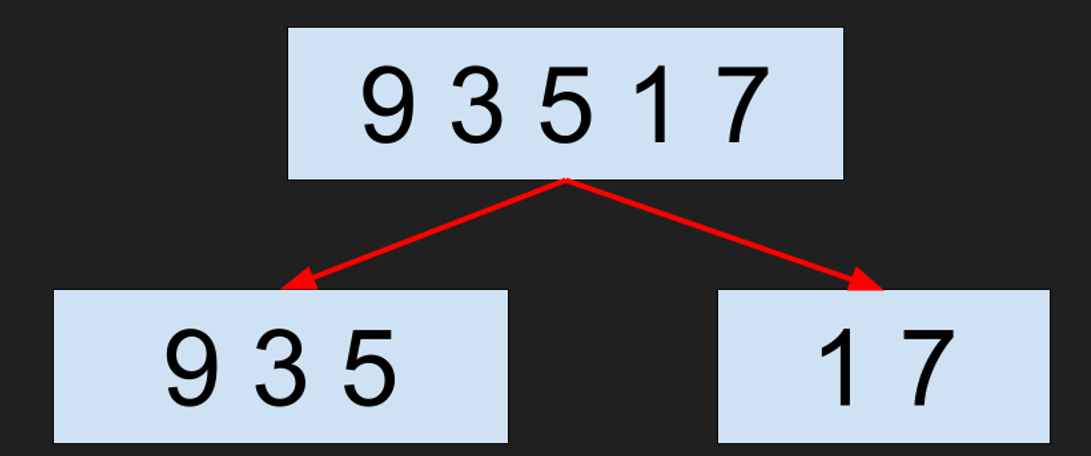
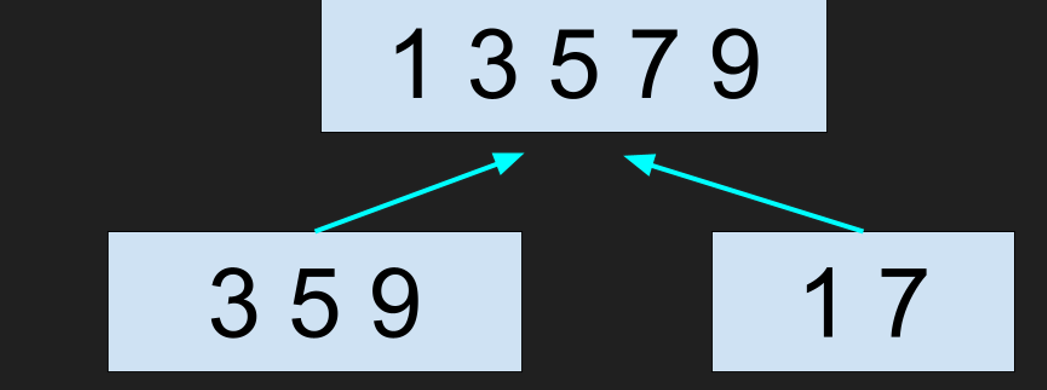
大まかなマージソートの動作のイメージ図は次のようになります。
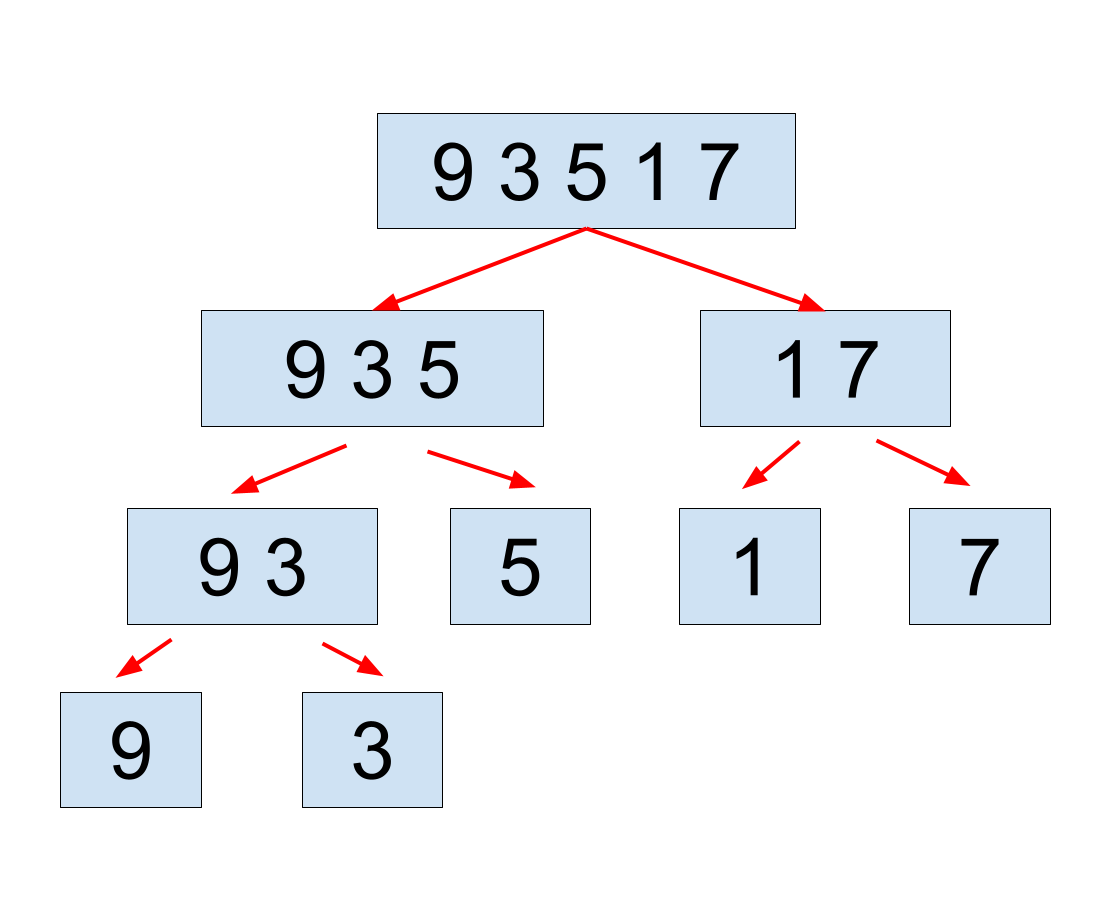
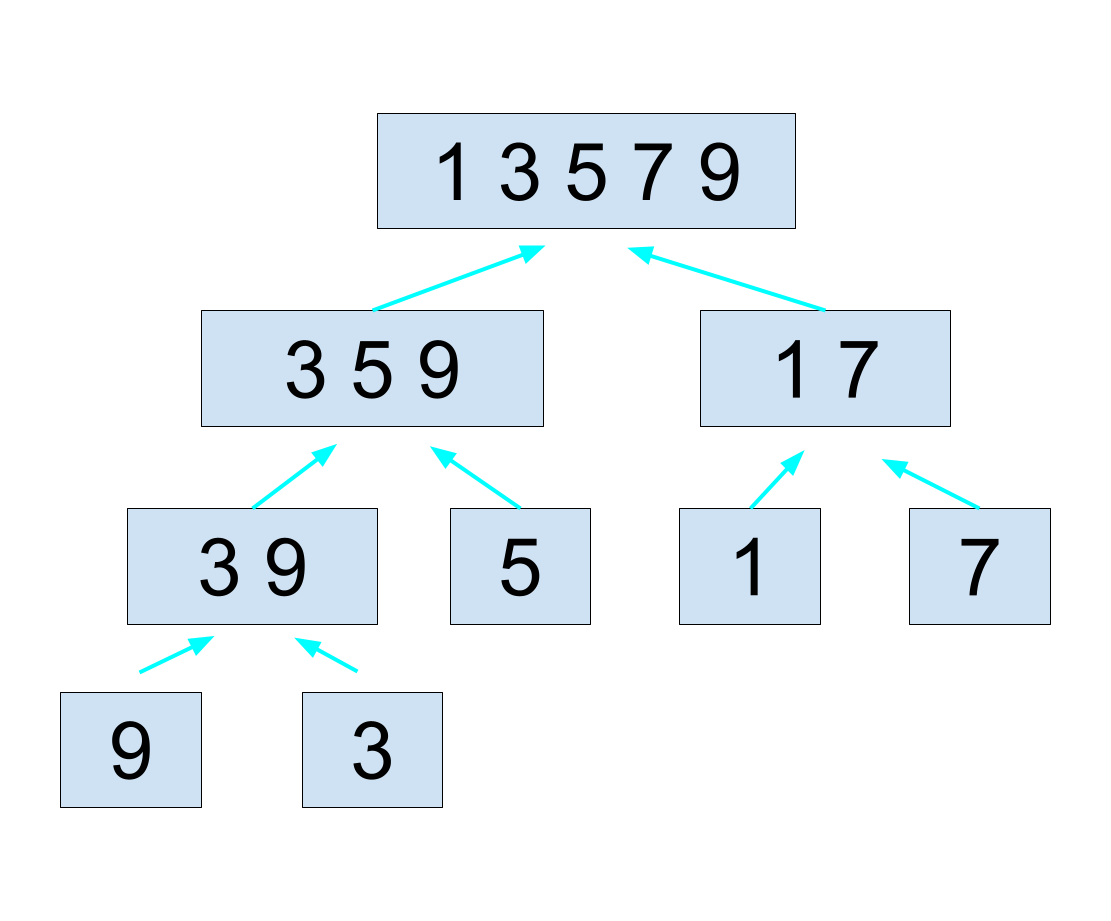
ただし、一気に全部分割しているのではなく、再帰的に分割されます。
2. マージソートのプログラム
def merge(A, p, q, r):
print(f"merge(A,{p},{q},{r})")
n1 = q - p + 1
n2 = r - q
L = [0] * n1
R = [0] * n2
for i in range(n1):
L[i] = A[p + i]
for j in range(n2):
R[j] = A[q + j + 1]
L.append(float('inf'))
R.append(float('inf'))
i = 0
j = 0
for k in range(p, r + 1):
if L[i] <= R[j]:
A[k] = L[i]
i += 1
else:
A[k] = R[j]
j += 1
def merge_sort(A, p, r):
if p < r:
q = (p + r) // 2
merge_sort(A, p, q)
merge_sort(A, q + 1, r)
merge(A, p, q, r)
A = [9,3,5,1,7]
print(A)
merge_sort(A, 0, len(A) - 1)
print(A)
2.1. merge_sort関数
merge_sort 関数はリスト A を再帰的に分割していく役割を持っています。具体的には、リストの中間点 q を見つけ、それを境にリストを分け、それぞれに対してさらに merge_sort を適用します。最終的には分割されたリストが十分小さくなった時点(配列の長さが1以下)で、merge 関数によってソートしながら結合されます。
2.2. merge関数
merge 関数は、merge_sort から分割されたリストを受け取り(実際はリストとその添え字を受け取る)、それらをソートしながら一つのリストに結合する役割を果たします。この関数では、二つの配列 L (左のリスト) と R (右のリスト) を使用し、それぞれに対して番兵として無限大の値 float('inf') を配列の末尾に追加します。インデックス i と j をそれぞれ L と R の先頭に置き、小さい方の要素から順に元の配列 A にコピーしていきます。
3. 実際に動作を確認する。
3.1. merge(A,0,0,1)
初期条件として、L=[9,$\infty$],R=[3,$\infty$]、(i,j)=(0,0)、kの値は0≤k≤1となります。
[1]k=0、(i,j)=(0,0)の場合
L[0]>R[0]となるので、L[i] <= R[j]はfalseである。
したがって、A[0]=R[0]=3、j=1となる。(else節)
[2]k=1、(i,j)=(0,1)の場合
L[0]<R[1]となるので、L[i] <= R[j]はtrueである。
したがって、A[1]=L[0]=9、i=1となる。(if節)
したがって、Aの0から1は[3,9]となり図のようになる。
3.2. merge(A,0,1,2)
merge(A,0,0,1)により、左の[9,3]の部分は[3,9]になっている。
初期条件として、L=[3,9,$\infty$],R=[5,$\infty$]、(i,j)=(0,0)、kの値は0≤k≤2となります。
[1]k=0、(i,j)=(0,0)の場合
L[0]<R[0]となるので、L[i] <= R[j]はtrueである。
したがって、A[0]=L[0]=3、i=1となる。(if節)
[2]k=1、(i,j)=(1,0)の場合
L[1]>R[0]となるので、L[i] <= R[j]はfalseである。
したがって、A[1]=R[0]=5、j=1となる。(else節)
[3]k=2、(i,j)=(1,1)の場合
L[1]<R[1]となるので、L[i] <= R[j]はtrueである。
したがって、A[2]=L[1]=9、i=2となる。(if節)
したがって、Aの0から2は[3,5,9]となり図のようになる。
3.3. merge(A,3,3,4)
初期条件として、L=[1,$\infty$],R=[7,$\infty$]、(i,j)=(0,0)、kの値は3≤k≤4となります。
[1]k=3、(i,j)=(0,0)の場合
L[0]<R[0]となるので、L[i] <= R[j]はtrueである。
したがって、A[3]=L[0]=1、i=1となる。(if節)
[2]k=4、(i,j)=(1,0)の場合
L[1]>R[0]となるので、L[i] <= R[j]はfalseである。
したがって、A[4]=L[0]=7、j=1となる。(else節)
3.4. merge(A,0,2,4)
初期条件として、L=[3,5,9$\infty$],R=[1,7,$\infty$]、(i,j)=(0,0)、kの値は0≤k≤4となります。
[1]k=0、(i,j)=(0,0)の場合
L[0]>R[0]となるので、L[i] <= R[j]はfalseである。
したがって、A[0]=R[0]=1、j=1となる。(else節)
[2]k=1、(i,j)=(0,1)の場合
L[0]<R[1]となるので、L[i] <= R[j]はtrueである。
したがって、A[1]=L[0]=3、i=1となる。(if節)
[3]k=2、(i,j)=(1,1)の場合
L[1]<R[1]となるので、L[i] <= R[j]はtrueである。
したがって、A[2]=L[1]=5、i=2となる。(if節)
[4]k=3、(i,j)=(2,1)の場合
L[2]>R[1]となるので、L[i] <= R[j]はfalseである。
したがって、A[3]=R[1]=7、j=2となる。(else節)
[5]k=4、(i,j)=(2,2)の場合
L[2]<R[2]となるので、L[i] <= R[j]はtrueである。
したがって、A[2]=L[2]=9、i=3となる。(if節)
したがってA=[1,3,5,7,9]となる。