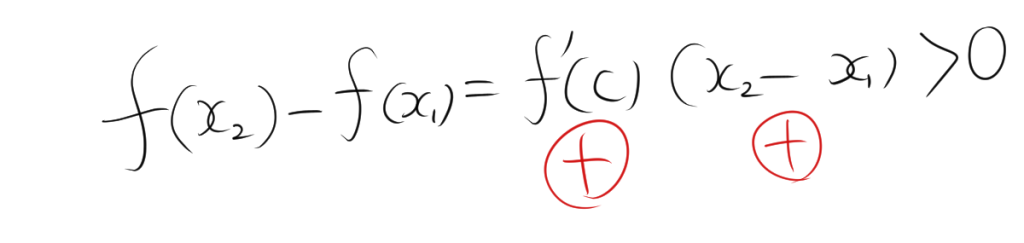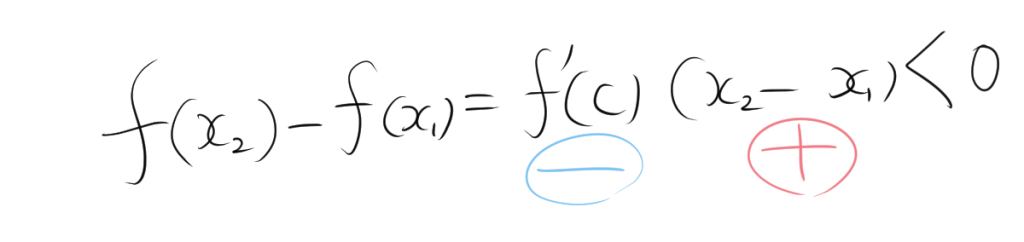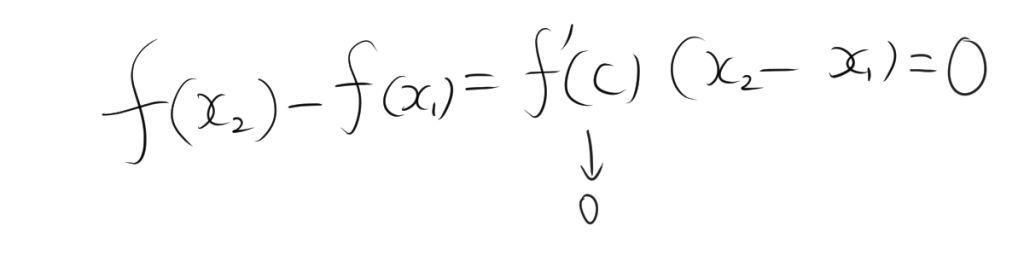単調増加と単調減少の意味と性質、判定について

はるか

単調増加…要は、値がずっと増えていく関数のこと。

ふゅか

そうね、\( f(x) = x^2 \) のように、区間 \( x \geq 0 \) では確かにずっと増加していくものね♪

はるか

うん。例えば、\( f(1) = 1^2 = 1 \)、\( f(2) = 2^2 = 4 \)、\( f(3) = 3^2 = 9 \)。確かに増加してる。

1. 単調増加

単調増加は、ある関数が「常に値が増加している」状態を指します。より正確には、任意の \( x_1 < x_2 \) に対して、関数 \( f(x) \) の値が \( f(x_1) \leq f(x_2) \) となる場合です。

1.1. 例

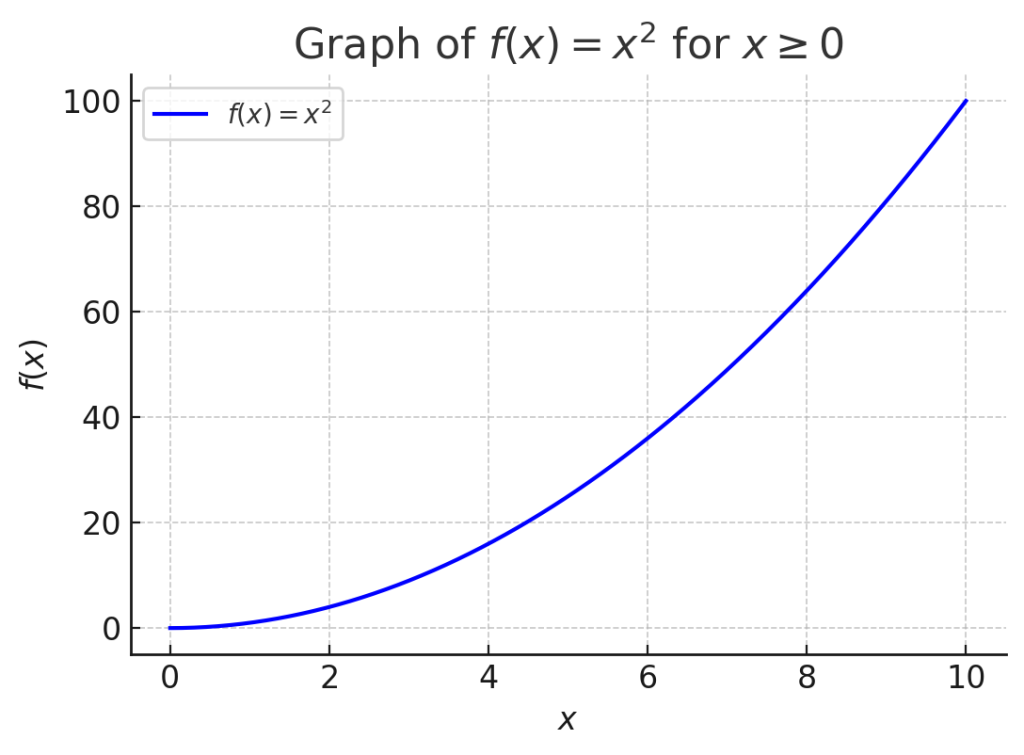
関数 \( f(x) = x^2 \) を考えましょう。この関数は、区間 \( x \geq 0 \) では単調増加です。つまり、\( x \) が増えると \( f(x) \) も増加します。

具体的に数値を見てみると、

• \( f(1) = 1^2 = 1 \)
• \( f(2) = 2^2 = 4 \)
• \( f(3) = 3^2 = 9 \)

このように、\( x \) の値が大きくなるにつれて、\( f(x) \) の値も大きくなります。

2. 単調減少

ふゅか

単調減少って、値がずっと減っていく関数のことよね。例えば、\( f(x) = -x \)！

はるか

そう。\( f(1) = -1 \)、\( f(2) = -2 \)、\( f(3) = -3 \)。値が小さくなってる。

ふゅか

\( x \) が増えると、\( f(x) \) は減るってことね。グラフを見るともっと分かりやすいかも！

単調減少は、関数が「常に値が減少している」状態です。任意の \( x_1 < x_2 \) に対して、\( f(x_1) \geq f(x_2) \) となる場合、その関数は単調減少関数と呼ばれます。

2.1. 例

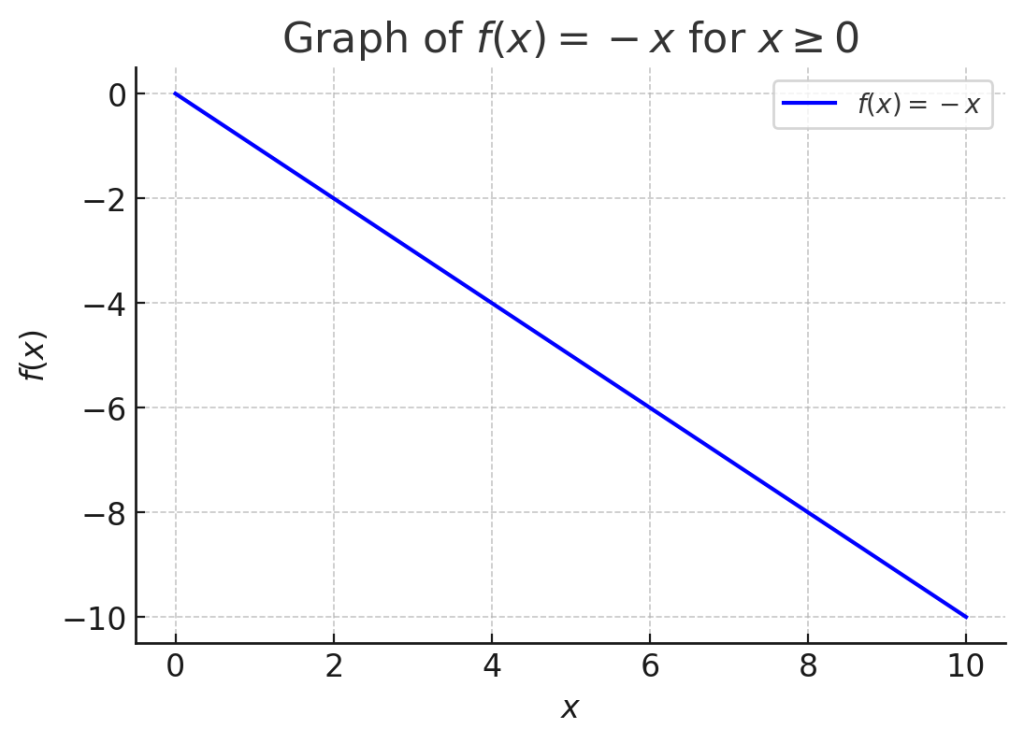
関数 \( f(x) = -x \) を考えます。この関数は、任意の \( x \) に対して単調減少です。つまり、\( x \) が増えると \( f(x) \) の値が減少します。

例えば、

• \( f(1) = -1 \)
• \( f(2) = -2 \)
• \( f(3) = -3 \)

このように、\( x \) が大きくなると、\( f(x) \) の値が減少していくのが確認できます。

3. 単調増加と単調減少における広義と狭義の意味

3.1. 単調増加の広義と狭義

\( f(x) = 2 \) という定数関数は、広義単調増加です。なぜなら、任意の \( x_1 < x_2 \) に対して \( f(x_1) = f(x_2) = 2 \) であり、増加または一定であるからです。

関数 \( f(x) = x + 1 \) は狭義単調増加です。任意の \( x_1 < x_2 \) に対して、必ず \( f(x_1) < f(x_2) \) となります。

はるか

広義の単調増加は、増えるか一定でいい。狭義だと、必ず増加。

ふゅか

そうね！\( f(x) = 2 \) は広義単調増加だけど、狭義にはならないってことね♪

3.2. 単調減少の広義と狭義

\( f(x) = -1 \) という定数関数は広義単調減少です。どの \( x_1 < x_2 \) においても \( f(x_1) = f(x_2) = -1 \) であり、値が減少もしくは一定であるためです。

関数 \( f(x) = -x \) は狭義の単調減少です。任意の \( x_1 < x_2 \) に対して、\( f(x_1) > f(x_2) \) が成立します。

4. 単調増加、減少と微分

微分を行うことで、単調増加と単調減少を判断することができます。

はるか

なんで、微分？？？？

ふゅか

実は、平均値の定理がかかわってくるから、微分がでてくるのよ！

4.1. \( f'(x) > 0 \) の場合 (単調増加の証明)

ある区間 \( I \) で \( f'(x) > 0 \) が常に成り立つと仮定します。任意の \( x_1, x_2 \in I \) に対して、\( x_1 < x_2 \) ならば、平均値の定理より、ある \( c \in (x_1, x_2) \) が存在して次の関係が成り立ちます。

\[ f(x_2) – f(x_1) = f'(c)(x_2 – x_1) \]

ここで、\( f'(c) > 0 \) 、$x_2-x_1>0$なので、\( f(x_2) – f(x_1) > 0 \)、つまり \( f(x_2) > f(x_1) \) です。よって、\( f(x) \) は \( I \) で単調増加します。

4.2. \( f'(x) < 0 \) の場合 (単調減少の証明)

同様に、ある区間 \( I \) で \( f'(x) < 0 \) が常に成り立つと仮定します。任意の \( x_1, x_2 \in I \) に対して、平均値の定理より、\( x_1 < x_2 \) であるとき、ある \( c \in (x_1, x_2) \) が存在して次の関係が成り立ちます。

\[ f(x_2) – f(x_1) = f'(c)(x_2 – x_1) \]

ここで、\( f'(c) < 0 \) 、$x_2-x_1>0$なので、\( f(x_2) – f(x_1) < 0 \)、つまり \( f(x_2) < f(x_1) \) です。したがって、\( f(x) \) は \( I \) で単調減少であることが証明されます。

4.3. \( f'(x) = 0 \) の場合 (定数関数の証明)

ある区間 \( I \) で \( f'(x) = 0 \) が常に成り立つと仮定します。この場合、\( f'(x) = 0 \) であるため、関数 \( f(x) \) の変化率は常にゼロです。これはつまり、関数 \( f(x) \) が \( I \) の任意の \( x \) に対して変化しないことを意味します。

任意の \( x_1, x_2 \in I \) に対して、平均値の定理より、\( x_1 < x_2 \) であるとき、ある \( c \in (x_1, x_2) \) が存在して次の関係が成り立ちます。

\[ f(x_2) – f(x_1) = f'(c)(x_2 – x_1) \]

ここで、\( f'(c) = 0 \) なので、\( f(x_2) – f(x_1) = 0 \)、つまり \( f(x_2) = f(x_1) \) です。よって、関数 \( f(x) \) は区間 \( I \) で定数です。