モンテカルロ法を使って円周率を計算してみよう

はるか

円周率をプログラムで求めてみたい。

ふゅか

そうね。モンテカルロ法を用いると比較的簡単に計算できるわよ。

1. モンテカルロ法

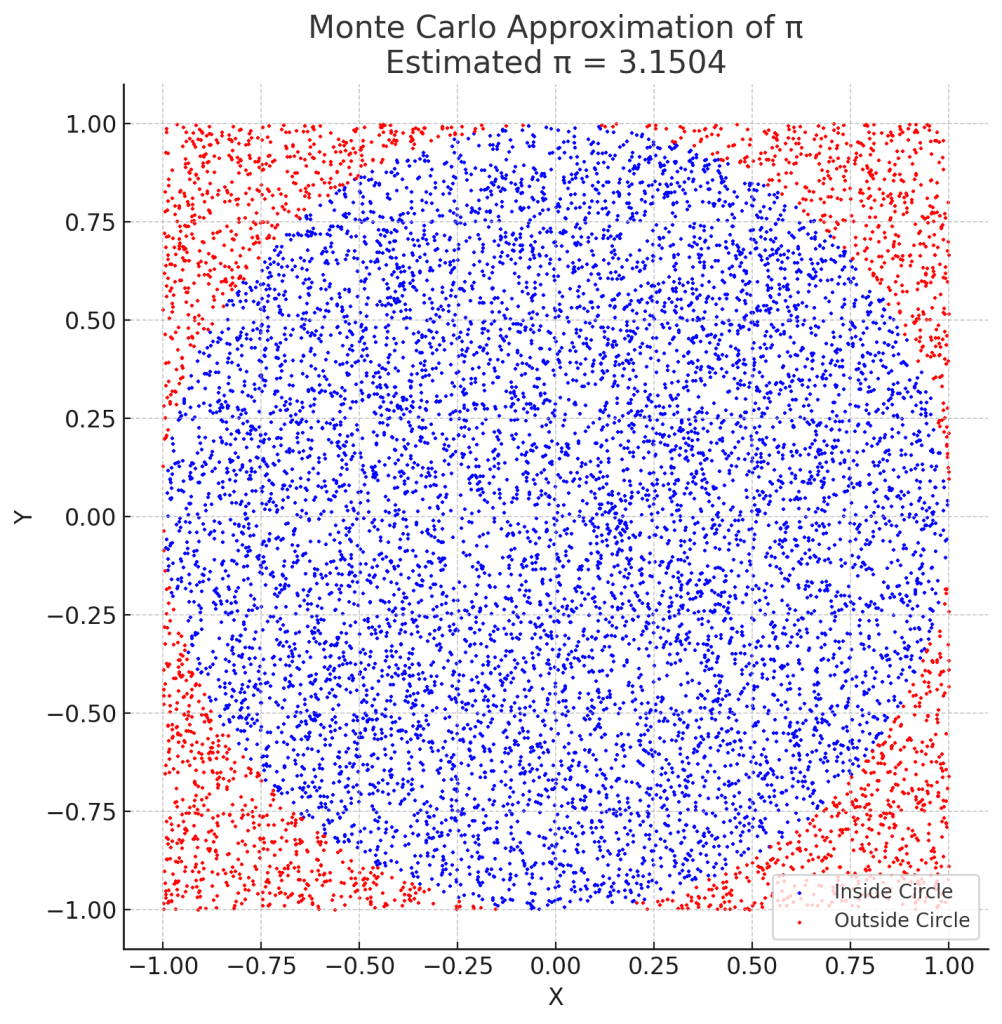
モンテカルロ法を用いて円周率（π）を求める方法は、乱数を用いて円の面積と正方形の面積の比率からπを近似的に求めるものです。

1.1. ステップ

モンテカルロ法では、次のようなステップを踏みます。

はるか

きれいに点がわかれるなぁ。

1.1.1. 正方形と円の設定

まず、半径が1の円を考えます。この円を囲む正方形を考えると、正方形の一辺の長さは2になります。したがって、正方形の面積は4（2×2）です。一方で、円の面積はπになります。

ふゅか

円と正方形に着目するのが肝だね！

1.1.2. ランダムな点を打つ

正方形の内部にランダムな点を多数打ちます。具体的には、x座標とy座標をランダムに生成し、その点が円の内部にあるかどうかを判定します。

1.1.3. 円の内部にある点の数を数える

点が円の内部にあるかどうかは、点の座標 (x, y) が次の条件を満たすかで判定できます。 \[ x^2 + y^2 \leq 1 \] この条件を満たす点が円の内部にあります。

1.1.4. 円周率の近似値を計算する

円の内部にある点の数を \( N_{\text{inside}} \)、全体の点の数を \( N_{\text{total}} \) とすると、円の面積と正方形の面積の比率は次のようになります。 \[ \frac{\pi}{4} \approx \frac{N_{\text{inside}}}{N_{\text{total}}} \] よって、これを用いてπの近似値を求めることができます。 \[ \pi \approx 4 \times \frac{N_{\text{inside}}}{N_{\text{total}}} \]

1.2. 実際の計算例

例えば、100万点のランダムな点を正方形内に打ち、そのうちの785398点が円の内部にあったとします。この場合、πの近似値は次のように求められます。

\[ \pi \approx 4 \times \frac{785398}{1000000} = 3.141592 \]

1.3. pythonコード

import random

def estimate_pi(num_samples):
    inside_circle = 0

    for _ in range(num_samples):
        x = random.uniform(-1, 1)
        y = random.uniform(-1, 1)
        
        # 円の内部にあるかどうかをチェック
        if x**2 + y**2 <= 1:
            inside_circle += 1

    # πの近似値を計算
    pi_estimate = 4 * inside_circle / num_samples
    return pi_estimate

# サンプル数を指定してπを求める
num_samples = 1000000
pi_estimate = estimate_pi(num_samples)
print(f"Estimated π: {pi_estimate}")

シード値を固定せず乱数を使用するため、値は同じになりません。