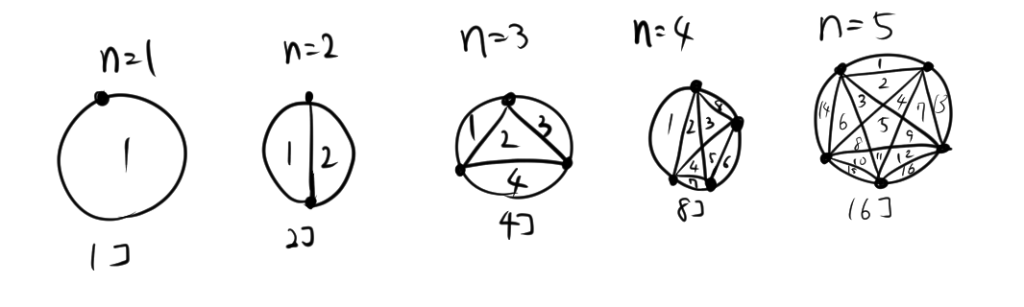モーザー数列とモーザーの円の分割問題の証明について

1. モーザーの円の分割問題

$M(n)$をモーザー数列と呼ぶ。

1.1. 実際に項を計算すると

モーザー数列の初めのいくつかの項は以下のようになります。

\[ M(1) = 1, \quad M(2) = 2, \quad M(3) = 4, \quad M(4) =8, \quad M(5) = 16, \quad \dots \]

このように、$1$から$5$までの間は$2^{n-1}$の様に振舞いますが、実際は違うんです。

2. 領域がどれだけ増えるのか

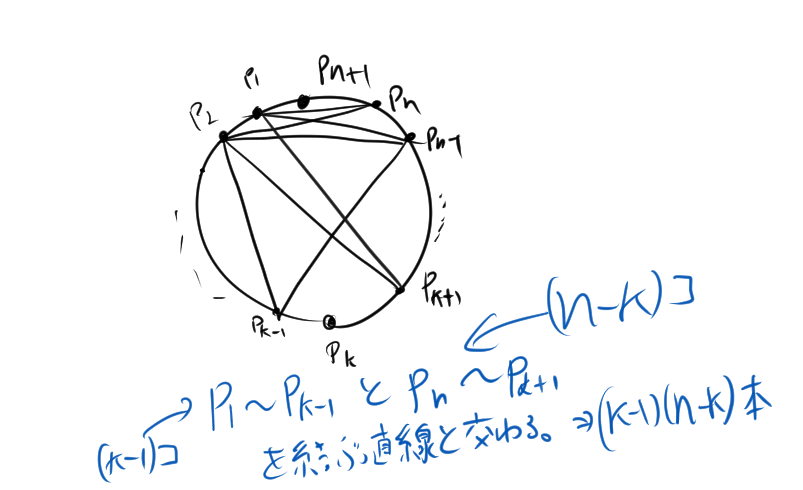
$P_1$から$P_n$までのn個の点がすでに打たれているとします。ここで、新たに点$P_{n+1}$を打つとしましょう。

点$P_{n+1}$から各点$P_k$に向かって新しい直線を引くと、この直線がすでに引かれている他の直線と交わるたびに領域が分割されます。このため、新しい直線を引き終えると領域が1つ増えます。

さらに、点$P_1$から点$P_{k-1}$までの点と、点$P_{k+1}$から点$P_n$までの点を結ぶ直線が存在します。これらの直線と新たに引いた直線が交わる箇所も領域を分割します。具体的には、点$P_1$から点$P_{k-1}$までの点と、点$P_{k+1}$から点$P_n$までの点の組み合わせにより、交わる直線の本数は$(k-1)(n-k)$本になります。

したがって、最終的に増える領域の数は、$(k-1)(n-k) + 1$個となります。

最終的にk=1からnまで試すため、増える領域の数の和は

$$\sum_{k=1}^n (k-1)(n-k) + 1$$

となる。

3. 漸化式を求める

最大の領域数を$M(n)$とすると、$M(n+1)$との差は増えた領域になるので

$$M(n+1) – M(n) = \sum_{k=1}^{n} (k-1)(n-k) + 1$$

3.1. シグマの計算

まず、シグマ部分を計算します。

\[ S(n) = \sum_{k=1}^{n} (k-1)(n-k)+1 \]

まず、与えられたシグマ部分を展開すると、

\[ S(n) = \sum_{k=1}^{n} ( – k^2  +kn+ k+1- n) \]

ここから、4つのシグマに分けて計算します。

\[ S(n) = n\sum_{k=1}^{n}k – \sum_{k=1}^{n}k^2+\sum_{k=1}^{n}1-n + \sum_{k=1}^{n}k \]

すべてのシグマを計算すると、

\[\begin{align*}S(n) &= n \times \frac{n(n+1)}{2} – \frac{n(n+1)(2n+1)}{6} – n^2 + n + \frac{n(n+1)}{2} \\ &= \frac{n^3+n^2}{2}- \frac{2n^3+3n^2+n}{6} +\frac{n^2+n}{2} – n^2 + n \\ &= \frac{3n^3+3n^2}{6}- \frac{2n^3+3n^2+n}{6} +\frac{3n^2+3n}{6} +\frac{ – 6n^2 + 6n}{6} \\ &= \frac{n^3-3n^2+8n}{6} \end{align*}\]

3.2. 階差数列の計算

漸化式は以下のようになります。

\[ M(n+1) – M(n) = \frac{n^3-3n^2+8n}{6} \]

したがって、階差数列の形になるので、$n\geq 2$では

$$\begin{align*} M(n) &= M(1) + \sum_{k=1}^{n-1} \left( M(k+1) – M(k) \right) \\ &= 1 + \sum_{k=1}^{n-1} \frac{k^3 – 3k^2 + 8k}{6} \\ &= 1 + \frac{1}{6} \sum_{k=1}^{n-1} \left( k^3 – 3k^2 + 8k \right) \end{align*}$$

各項の和を計算します。

$$\begin{align*} \sum_{k=1}^{n-1} \left( k^3 – 3k^2 + 8k \right) &= \sum_{k=1}^{n-1} k^3 – 3\sum_{k=1}^{n-1} k^2 + 8\sum_{k=1}^{n-1} k \\ &= \left( \frac{(n-1)n}{2} \right)^2 – 3 \left( \frac{(n-1)n(2n -1)}{6} \right) + 8 \left( \frac{(n-1)n}{2} \right) \end{align*}$$

これらをまとめて、

$$\begin{align*} \sum_{k=1}^{n-1} \left( k^3 – 3k^2 + 8k \right) &= \frac{(n-1)^2 n^2}{4} – \frac{(n-1)n(2n -1)}{2} + 4(n-1)n \end{align*}$$

整理します。

$$\begin{align*} &= \frac{1}{4} \left[ (n-1)^2 n^2 – 2(n-1)n(2n -1) + 8(n-1)n \times 2 \right] \\ &= \frac{1}{4} (n-1)n \left[ n(n-1) – 2(2n -1) + 16 \right] \end{align*}$$

したがって、

$$\begin{align*} \sum_{k=1}^{n-1} \left( k^3 – 3k^2 + 8k \right) &= \frac{(n-1)n (n^2 – 5n + 18)}{4} \end{align*}$$

これを \( M(n) \) の式に代入します。

$$\begin{align*} M(n) &= 1 + \frac{1}{6} \times \frac{(n-1)n (n^2 – 5n + 18)}{4} \\ &= 1 + \frac{(n-1)n (n^2 – 5n + 18)}{24} \end{align*}$$

したがって、\( M(n) \)を展開すると次のようになります。

$$\begin{align*} M(n) &= 1 + \frac{n^4 – 6n^3 + 23n^2 – 18n}{24} \end{align*}$$

最後に、

$$\begin{align*} M(n) &= \frac{24}{24} + \frac{n^4 – 6n^3 + 23n^2 – 18n}{24} \\ &= \frac{n^4 – 6n^3 + 23n^2 – 18n + 24}{24} \end{align*}$$

$n=1$でも成り立つため、$n\geq1$のとき

$$\begin{align*} M(n) &= \frac{n^4 – 6n^3 + 23n^2 – 18n + 24}{24} \end{align*}$$