Muirheadの不等式の証明と記号の意味について

1. 必要な記号

Muirheadの不等式を理解するためには、以下の3つの記号を理解する必要があります。

$\large\displaystyle\sum_{\mathrm{sym}}$

$[a,b,c]$

$\succeq$

これらが理解できれば、Muirheadの不等式の意味が分かります。また、Muirheadの不等式はムーアヘッドの不等式と呼ばれることがあります。

2. $\displaystyle\sum_{\mathrm{sym}}$

$\large\displaystyle\sum_{\mathrm{sym}}$という記号はsymmetric sumを表す数学的な記号です。

symmetric sumとは、項の順序を入れ替えたときに同じ値をとる式に対して、各項の和を求めたものです。
３変数を用いる場合、$\large\displaystyle\sum_{\mathrm{sym}} f(x,y,z)$ は、以下のように計算されます。

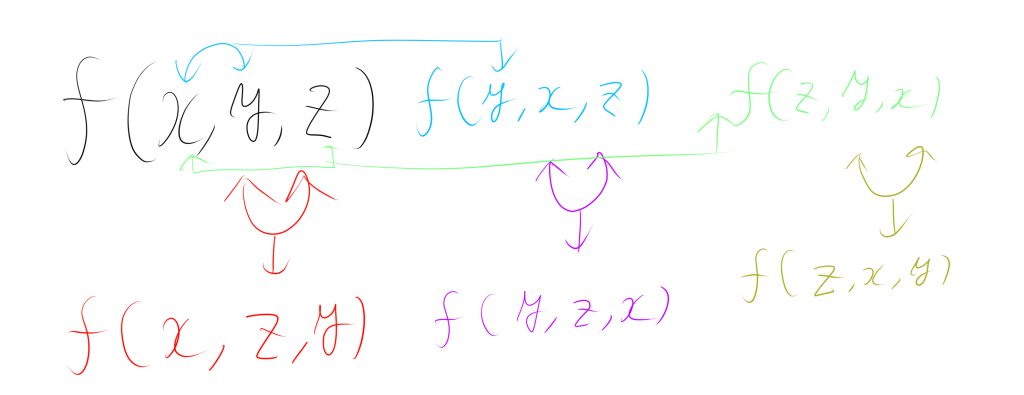
$\displaystyle\sum_{\mathrm{sym}} f(x,y,z) = f(x,y,z) + f(x,z,y) + f(y,x,z) + f(y,z,x) + f(z,x,y) + f(z,y,x)$

つまり、各項の変数の順序を全て考慮し、和を求めたものです。$3!$通りの組み合わせとなります。図のような組み合わせとなります。

一方、$n$変数を用いる場合、$n!$通りの組み合わせの和となります。

2.1. symmetric sumの例題

$(1)$与えられた式 $f(x,y) = x+y^2$ を 代入すると、$x,y$ という2つの変数を考慮して、以下のように展開されます。

$$\begin{align*} \sum_{\mathrm{sym}} f(x, y) &= f(x, y) + f(y, x) \\ &= (x + y^2) + (y + x^2) \\ &= x + y + x^2 + y^2 \end{align*}$$

$(2)$与えられた式 $f(x,y,z) = x^2+y^2+z^2$ を代入すると、

$$\displaystyle\sum_{\mathrm{sym}} f(x,y,z)  = (x^2+y^2+z^2) + (x^2+z^2+y^2) + (y^2+x^2+z^2) + (y^2+z^2+x^2) + (z^2+x^2+y^2) + (z^2+y^2+x^2)$$

となります。各項の $x^2, y^2, z^2$ の係数をまとめると、

$$\displaystyle\sum_{\mathrm{sym}} f(x,y,z)=6(x^2+y^2+z^2)$$

となります。

$(3)$与えられた式 $f(x,y,z) = xyz$ を $\large\displaystyle\sum_{\mathrm{sym}}$ に代入すると、

$$\displaystyle\sum_{\mathrm{sym}} f(x,y,z) = xyz + xzy + yxz + yzx + zxy + zyx$$

となります。項の並びを整理すると、

$$\displaystyle\sum_{\mathrm{sym}} f(x,y,z)=6xyz$$

3. $[a,b,c]$

数列$[a,b,c]$と3変数を用いる場合$x$ を $a$ 回、$y$ を $b$ 回、$z$ を $c$ 回乗じた項の対称和を表します。つまり、数列が$[a,b,c]$であるときの対称和は

$\displaystyle\sum_{\mathrm{sym}}x^ay^bz^c$

3.1. majorize

majorizeとは非負数からなる2つの数列$\mathbf{a}$と$\mathbf{b}$の関係を示します。ただし、数列$\mathbf{a}$と$\mathbf{b}$の要素はそれぞれ以下の条件を満たしています。

$a_1 \geq a_2 \geq \cdots \geq a_{n-1} \geq a_n \geq 0$

具体的には、以下の条件が満たされる場合に、$\mathbf{a}　\mathrm{mjorize}　\mathbf{b}$といい、$[\mathbf{a}] \succeq [\mathbf{b}]$と表記します。

両方の数列の和が等しい：すなわち、$\displaystyle\sum_{i=1}^n a_i = \displaystyle\sum_{i=1}^n b_i$

任意の$k$（$1\leq k\leq n-1$）について、以下が成り立つ：$\displaystyle\sum_{i=1}^{k}a_{k}\geq \displaystyle\sum_{i=1}^{k}b_{k}$

3.2. majorizeの例題

以下では下記の通りに$\mathbf{a}$と$\mathbf{b}$を表す。

$\mathbf{a}=[a_1,\cdots,a_n]$

$\mathbf{b}=[b_1,\cdots,b_n]$

$(1)$まず、数列の和を調べます。

$\displaystyle\sum_{i=1}^3 a_i = 4+3+1=8$

$\displaystyle\sum_{i=1}^3 b_i = 2+2+2=6$

この結果から、$\mathbf{a}$と$\mathbf{b}$の数列の和が等しくないことが分かります。したがって、$\mathbf{a}　\mathrm{ mjorize }　\mathbf{b}$ではない。

$(2)$まず、数列の和を調べます。

$\displaystyle\sum_{i=1}^2 a_i =2+0=2$

$\displaystyle\sum_{i=1}^2 b_i = 1+1=2$

この結果から、$\mathbf{a}$と$\mathbf{b}$の数列の和が等しいことが分かります。次に、$\mathbf{a}$と$\mathbf{b}$の部分和を比較してみます。

$a_1=2\geq 1 =b_1$

この結果から、$\mathbf{a}　\mathrm{ mjorize }　\mathbf{b}$となるため、$\mathbf{a}\succeq\mathbf{b}$となります。

$(3)$まず、数列の和を調べます。

$\displaystyle\sum_{i=1}^3 a_i =2+0+1=3$

$\displaystyle\sum_{i=1}^3 b_i = 1+1+1=3$

この結果から、$\mathbf{a}$と$\mathbf{b}$の数列の和が等しいことが分かります。次に、$\mathbf{a}$と$\mathbf{b}$の部分和を比較してみます。

$a_1=2\geq 1 =b_1$

$a_1+a_2=2\geq 2=b_1+b_2$

この結果から、$\mathbf{a}　\mathrm{ mjorize }　\mathbf{b}$となるため、$\mathbf{a}\succeq\mathbf{b}$となります。

4. Muirheadの不等式

4.1. 不等式の意味を理解する

まず、$\displaystyle\prod^{n}_{i=1} x_i^{a_i}$はどういう意味なのかというと、$x_1^{a_1}$から$x_n^{a_n}$までの積です。つまり、

$\displaystyle\prod^{n}_{i=1} x_i^{a_i}=x_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}$

となるため、$\displaystyle\sum_{\mathrm{sym}}x_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}$となります。

これがさっきまでの話にどうつながるのかというと、$\displaystyle\sum_{\mathrm{sym}}x_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}$は、$[a_1,a_2,\cdots,a_n]$とあら合わすことができます。

4.2. Muirheadの不等式の具体例

$[2,0,1]\succeq[1,1,1]$の場合、次の不等式が成り立ちます。

$$\sum_{\mathrm{sym}} x^2 z \geq \sum_{\mathrm{sym}} xyz$$

$[2,0,1]$のときのsymmetric sumを求めると、

$$ \sum_{\mathrm{sym}} x^2 z = x^2 z + x^2 y + y^2 z + y^2 x + z^2 y + z^2 x $$

$[1,1,1]$のときのsymmetric sumを次に求めると、

$$\sum_{\mathrm{sym}} xyz = 6xyz$$

となるため、

$$x^2z+x^2y+y^2z+y^2x+z^2y+z^2x \geq 6xyz$$

となる。

$[4,0,0,0]\succeq[1,1,1,1]$の場合、次の不等式が成り立ちます。

$$\sum_{\mathrm{sym}} x^4 \geq  \sum_{\mathrm{sym}} xyzw$$

$[4,0,0,0]$のときのsymmetric sumを求めると、

$$\sum_{\mathrm{sym}} x^4= 6x^4 + 6y^4 + 6z^4 + 6w^4$$

$[1,1,1,1]$のときのsymmetric sumを次に求めると、

$$\sum_{\mathrm{sym}} xyzw= 24xyzw$$

となるため、次の不等式が成り立ちます。

$$x^4+y^4+z^4+w^4 \geq 4xyzw$$

ここから少し、本筋からずれます。

5. 置換の和

$\displaystyle\sum_{\sigma}f(x_{\sigma(1)},\cdots x_{\sigma(n)})$ は、置換 による和を表します。ここで $\sigma$ は、置換を表す記号で、要素の並び順を入れ替える操作を表します。$\sigma(n)$は、置換$\sigma$によって$n$がどの要素に対応するかを表します。たとえば、$\sigma=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 1 & 3 & 2 & 5 & 4\end{pmatrix}$であれば、$\sigma(1)=1$、$\sigma(2)=3$、$\sigma(3)=2$、$\sigma(4)=5$、$\sigma(5)=4$となります。

つまり、

$$\displaystyle\sum_{\mathrm{sym}} f(x,y,z) = f(x,y,z) + f(x,z,y) + f(y,x,z) + f(y,z,x) + f(z,x,y) + f(z,y,x)$$

に対して

$$\displaystyle\sum_{\sigma}f(x_{\sigma(1)},\cdots x_{\sigma(n)})$$

を用いて表すことができます。具体的には、

$$\displaystyle\sum_{\mathrm{sym}} f(x,y,z) = \displaystyle\sum_{\sigma}f(x_{\sigma(1)},x_{\sigma(2)}, x_{\sigma(3)})$$

つまり、変数が$n$個のときは、

$$\displaystyle\sum_{\mathrm{sym}} f(x_1,x_2,\cdots x_n) = \displaystyle\sum_{\sigma}f(x_{\sigma(1)},x_{\sigma(2)},\cdots x_{\sigma(n)})$$

とあらわすことができる。

5.1. 置換の和の例題

$$\begin{align*}&\displaystyle\sum_{\sigma} x_{\sigma(1)}+x_{\sigma(2)}+x_{\sigma(3)} \\&= (x_1+x_2+x_3)+(x_1+x_3+x_2)+(x_2+x_1+x_3)+(x_2+x_3+x_1)+(x_3+x_1+x_2)+(x_3+x_2+x_1) \\&=(x+y+z)+(x+z+y)+(y+x+z)+(y+z+x)+(z+x+y)+(z+y+x) \\& = 6(x+y+z)\end{align*}$$

ここで、$\sigma$ による置換の種類は

$$(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)$$

となります。

6. symmetric function と symmetric sum

$n$個の変数に関するsymmetric functionとは、その変数の任意の置換によって不変な関数のことを指します。

つまり、置換した後も関数が変わらないため、$f(x_1,x_2,\cdots x_n)$を$n!$回足していることになる。数式で表すと、

$$\displaystyle\sum_{\sigma}f(x_{\sigma(1)},x_{\sigma(2)},\cdots x_{\sigma(n)})=n!f(x_1,x_2,\cdots x_n)$$

となる。つまり、

$$\displaystyle\sum_{\mathrm{sym}} f(x_1,x_2,\cdots x_n) = n!f(x_1,x_2,\cdots x_n)$$

となる。

6.1. Muirheadの不等式におけるsymmetric functionの具体例

例えば、Muirheadの不等式の具体例で示した、$[1,1,1,1]$の$xyzw$の係数は$4!$となったり、$[1,1,1]$の$xyz$の係数は$3!$となっていたりする。