正n角形の面積の公式の証明や具体例について

1. 正$n$角形の面積
正$n$角形の面積を$S_n$、その1辺の長さを$a$とすると、以下の公式で面積が求められます。
\[ S_n=\dfrac{na^2}{4\tan\dfrac{\pi}{n}} \quad (n \geq 3) \]
2. 証明
まず、正$n$角形の外心を$O$とします。この外心$O$から$n$個の頂点に向かって線分を引くと、正$n$角形は$n$個の合同な三角形に分割されます。それぞれの三角形の底辺の長さは、正$n$角形の1辺の長さ$a$です。
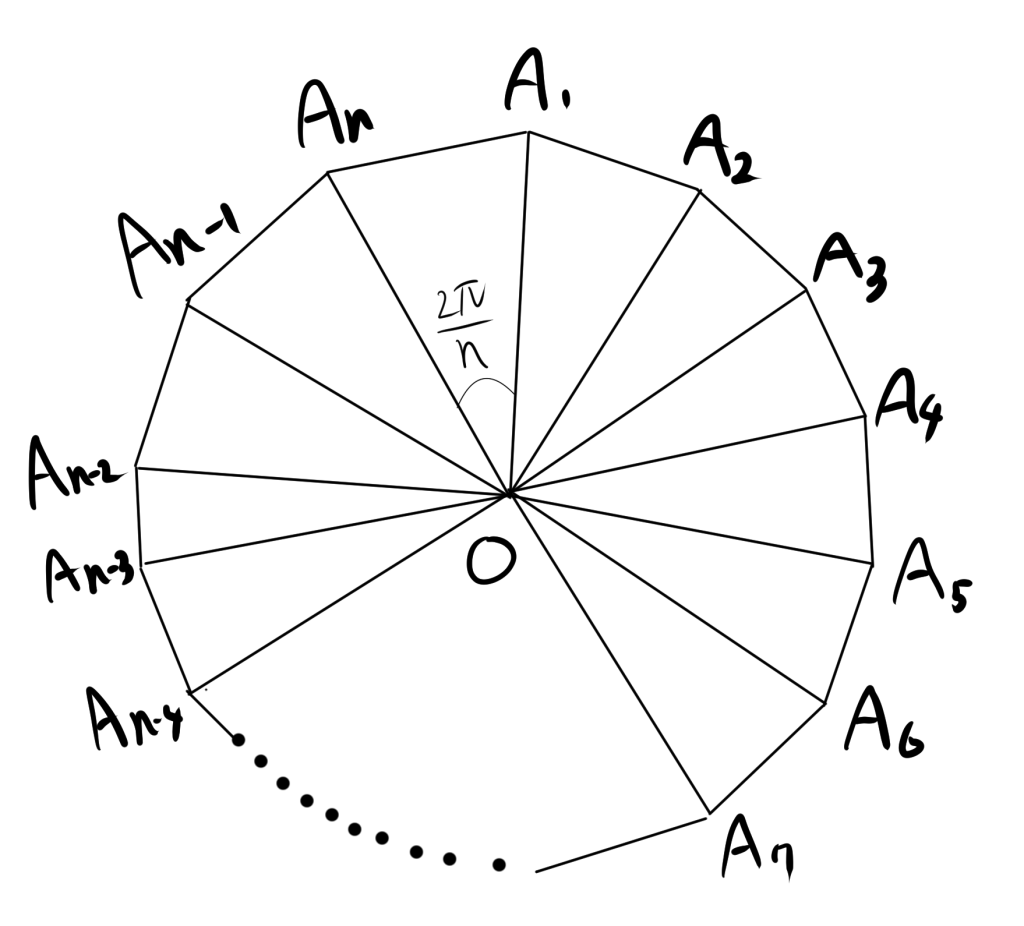
ここで、三角形$A_nOA_1$に注目します。三角形の底辺は$a$で、$\angle A_nOA_1$は$n$等分された角度の一つなので、その角度は$\frac{2\pi}{n}$です。
また、$O$から辺$A_1A_n$に垂線を引き、その交点を$M$とします。この三角形$A_nOA_1$は二等辺三角形なので、$A_nM = \dfrac{a}{2}$です。
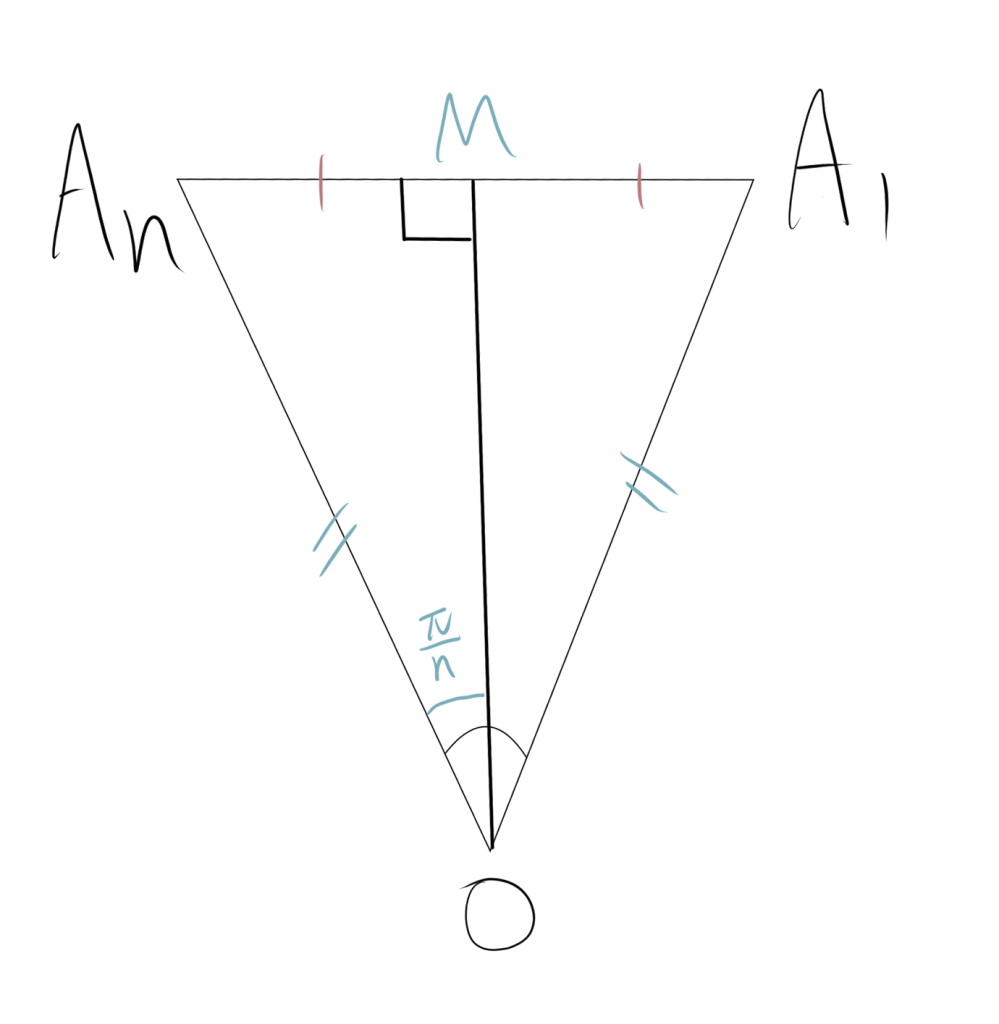
$\triangle A_nOM$において、$\angle A_nOM = \dfrac{\pi}{n}$です。三角比の定義より、
\[ \tan \dfrac{\pi}{n} = \dfrac{A_nM}{OM} = \dfrac{\dfrac{a}{2}}{OM} \]
これを解いて、$OM$の長さを求めます。
\[ OM = \dfrac{a}{2\tan\dfrac{\pi}{n}} \]
したがって、三角形$A_nOA_1$の面積$S$は、
\[ S = \dfrac{1}{2} \times A_nA_1 \times OM = \dfrac{1}{2} \times a \times \dfrac{a}{2\tan\dfrac{\pi}{n}} = \dfrac{a^2}{4\tan\dfrac{\pi}{n}} \]
この三角形が$n$個あるので、正$n$角形全体の面積$S_n$は、
\[ S_n = n \times S = \dfrac{na^2}{4\tan\dfrac{\pi}{n}} \]
別の方法として、正$n$角形の外接円の半径$R$を使った面積の求め方もあります。外接円の半径$R$を用いると、三角形$A_nOA_1$の面積$S$は、
\[ S = \dfrac{R^2}{2}\sin\dfrac{2\pi}{n} \]
となり、正$n$角形の面積$S_n$は
\[ S_n = nS = \dfrac{nR^2}{2}\sin\dfrac{2\pi}{n} \]
3. 実際に使ってみる
3.1. $n=3$(正三角形)のとき
$\tan \dfrac{\pi}{3} = \sqrt{3} $より、正三角形の面積$S_3$は
\[ S_3 = \dfrac{3a^2}{4\tan\dfrac{\pi}{3}} = \dfrac{\sqrt{3}a^2}{4} \]
3.2. $n=4$(正方形)のとき
$\tan \dfrac{\pi}{4} = 1$より、正方形の面積$S_4$は
\[ S_4 = \dfrac{4a^2}{4\tan\dfrac{\pi}{4}} = a^2 \]
3.3. $n=5$(正五角形)のとき
$\tan \dfrac{\pi}{5} = \sqrt{5 – 2 \sqrt{5}}$より、正五角形の面積$S_5$は
\[ S_5 = \dfrac{5a^2}{4\tan\dfrac{\pi}{5}} = \dfrac{5a^2}{4\sqrt{5 – 2 \sqrt{5}}} \]
\[ = \dfrac{5\sqrt{5 + 2 \sqrt{5}}a^2}{4\sqrt{5 – 2 \sqrt{5}}\sqrt{5 + 2 \sqrt{5}}} = \dfrac{5\sqrt{5 + 2 \sqrt{5}}a^2}{4\sqrt{5}} \]
\[ = \dfrac{\sqrt{5}\sqrt{5 + 2 \sqrt{5}}a^2}{4} = \dfrac{\sqrt{25+10\sqrt{5}}}{4}a^2 \]
これらの結果を使うことで、正$n$角形の面積を簡単に求めることができます。




