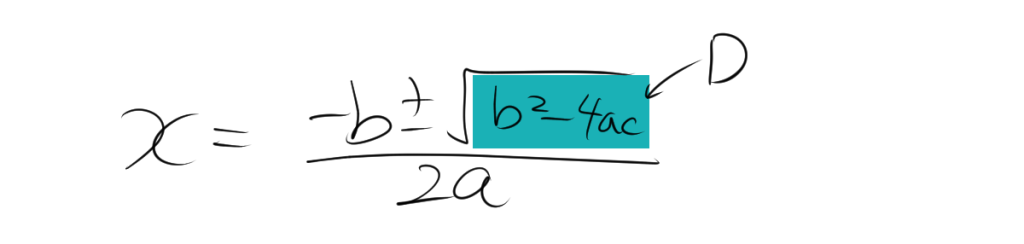【二次方程式】判別式の意味と例題について

ふゅか

判別式って、二次方程式の解の種類を決める重要な要素よね！Dがどうなるかで、解の数や種類がわかるの、面白いわ♪

はるか

そう。$D$が正なら実数解が2つ、ゼロなら重解、負なら虚数解になる。

1. 判別式

はるか

判別式Dの意味…二次方程式の解の公式と関係がある。

1.1. Dの意味

二次方程式の解の公式より、

となりますが、判別式$b^{2}-4ac$とはルートの中身を意味します。

1. $b^{2}-4ac > 0$ の場合

判別式が正の値なので、$\sqrt{b^{2}-4ac}$ は実数になります。このとき、解は

$$x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}$$

$\pm$ の符号により、二つの異なる実数解をもつ

2. $b^{2}-4ac = 0$ の場合

判別式がゼロなので、平方根の部分は $\sqrt{0} = 0$ となります。したがって、解は

$$x=\dfrac{-b}{2a}$$

となり、重解（重複する一つの実数解）を持ちます。

3. $b^{2}-4ac < 0$ の場合

判別式が負の値になるため、平方根の中身が負数となります。この場合、$\sqrt{b^{2}-4ac}$ は虚数になり、実数解を持ちません。

2. 判別式の例題

2.1. 例題1：異なる2つの実数解を持つ

与えられた2次方程式は \( 2x^2 – 3x – 5 = 0 \) です。ここで、係数は \( a = 2 \), \( b = -3 \), \( c = -5 \) です。

判別式 \( D \) は次のように計算されます

\[ D = (-3)^2 – 4 \times 2 \times (-5) = 9 + 40 = 49 \]

よって、\( D = 49 \) なので \( D > 0 \) です。この方程式は異なる2つの実数解を持ちます。

2.2. 例題2：重解

与えられた2次方程式は \( x^2 – 6x + 9 = 0 \) です。ここで、係数は \( a = 1 \), \( b = -6 \), \( c = 9 \) です。

判別式 \( D \) は次のように計算されます

\[ D = (-6)^2 – 4 \times 1 \times 9 = 36 – 36 = 0 \]

よって、\( D = 0 \) なのでこの方程式は重解を持ち、解は \( x = -\dfrac{b}{2a} = \dfrac{6}{2} = 3 \) です。

2.3. 例題3：虚数解を持つ

与えられた2次方程式は \( x^2 + 2x + 5 = 0 \) です。ここで、係数は \( a = 1 \), \( b = 2 \), \( c = 5 \) です。

判別式 \( D \) は次のように計算されます： \[ D = 2^2 – 4 \times 1 \times 5 = 4 – 20 = -16 \]

よって、\( D = -16 \) なので \( D < 0 \) です。この方程式は実数解を持たず、虚数解を持ちます。