二次関数のグラフの平行移動と3つの例題について

1. 二次関数の基本形
二次関数について復習しましょう。
\[ y = ax^2 + bx + c \]
- \( a > 0 \):下に凸な放物線
- \( a < 0 \):上に凸な放物線
2. 平行移動
平行移動とは、グラフ全体をある方向にその形を変えずに動かす操作です。二次関数の場合、グラフを x 軸方向や y 軸方向に動かすことができます。
2.1. y 軸方向の平行移動
y 軸方向に平行移動するには、関数全体に定数を加えます。例えば、関数 \( y = ax^2 + bx + c \) を \( k \) だけ y 軸方向に移動する場合、次のように式が変わります。
\[ y = ax^2 + bx + c + k \]
これは、グラフを上に \( k \) だけ(\( k > 0 \) の場合)または下に \( k \) だけ(\( k < 0 \) の場合)移動することを意味します。
2.2. x 軸方向の平行移動
次に、x 軸方向に平行移動する場合を考えます。x 軸方向に \( h \) だけ移動させたい場合、x の部分を \( (x – h) \) に置き換えます。すると、次のようになります。
\[ y = a(x – h)^2 + b(x – h) + c \]
これは、グラフを右に \( h \) だけ(\( h > 0 \) の場合)または左に \( h \) だけ(\( h < 0 \) の場合)移動することを意味します。
3. 平行移動の例
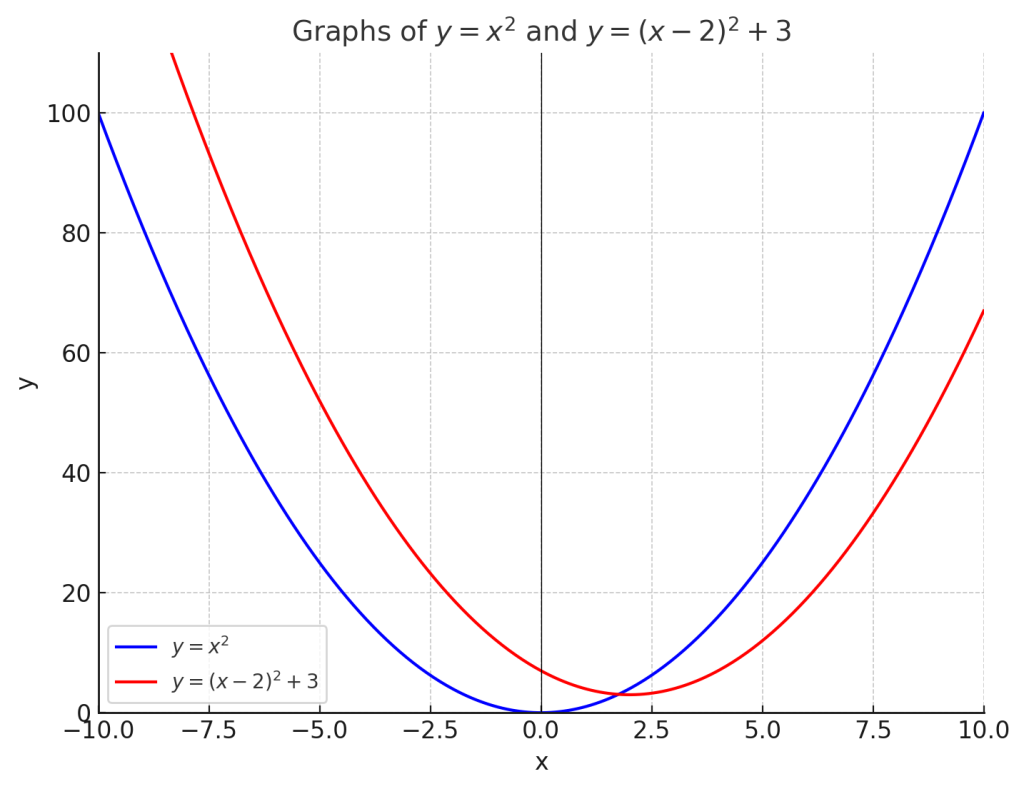
\( y = x^2 \) を平行移動していきます。
y 軸方向に 3 だけ上に移動すると、関数は次のように変わります。
\[ y = x^2 + 3 \]
x 軸方向に 2 だけ右に移動すると、関数は次のように変わります。
\[ y = (x – 2)^2 \]
両方を組み合わせて、y 軸方向に 3 だけ上に、x 軸方向に 2 だけ右に移動すると、次のような式になります。
\[ y = (x – 2)^2 + 3 \]
4. 二次関数の平行移動の例題
4.1. 例題 1:グラフの描画
\( x \)-軸方向に 3 だけ平行移動 → \( y = (x +3)^2 \)
\( y \)-軸方向に -2 だけ平行移動 → \( y = (x + 3)^2 – 2 \)
したがって、平行移動後の二次関数は
\[ y = (x + 3)^2 – 2 \]
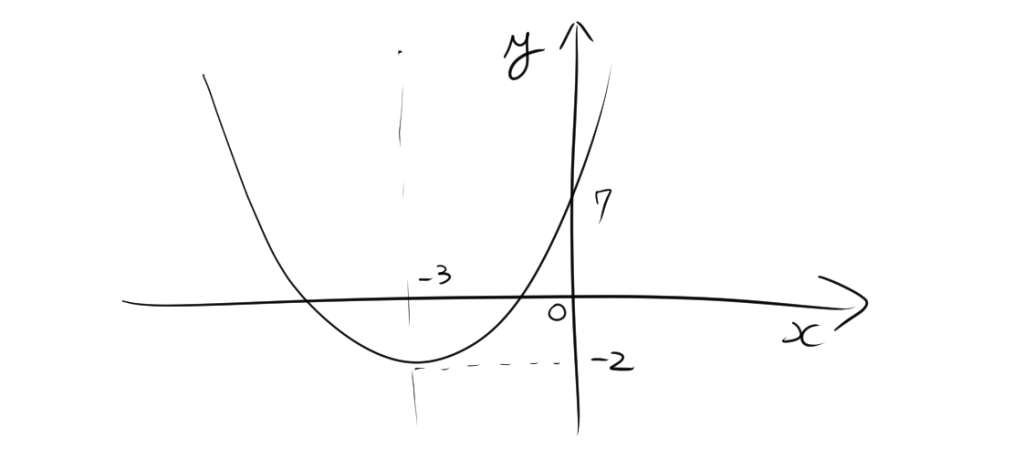
となります。頂点は$(-3,-2)$であることがわかります。一方で、式を展開すると、
\[ y =x^2+6x+7 \]
よって、y軸との交点は(0,7)であることがわかる。したがって、グラフを書くと、
4.2. 例題 2:二次関数の式
\( x \)-軸方向に -1 だけ平行移動 → \( y = -2(x + 1)^2 + 4(x + 1) – 1 \)
\( y \)-軸方向に 5 だけ平行移動 → \( y = -2(x + 1)^2 + 4(x + 1) – 1 + 5 \)
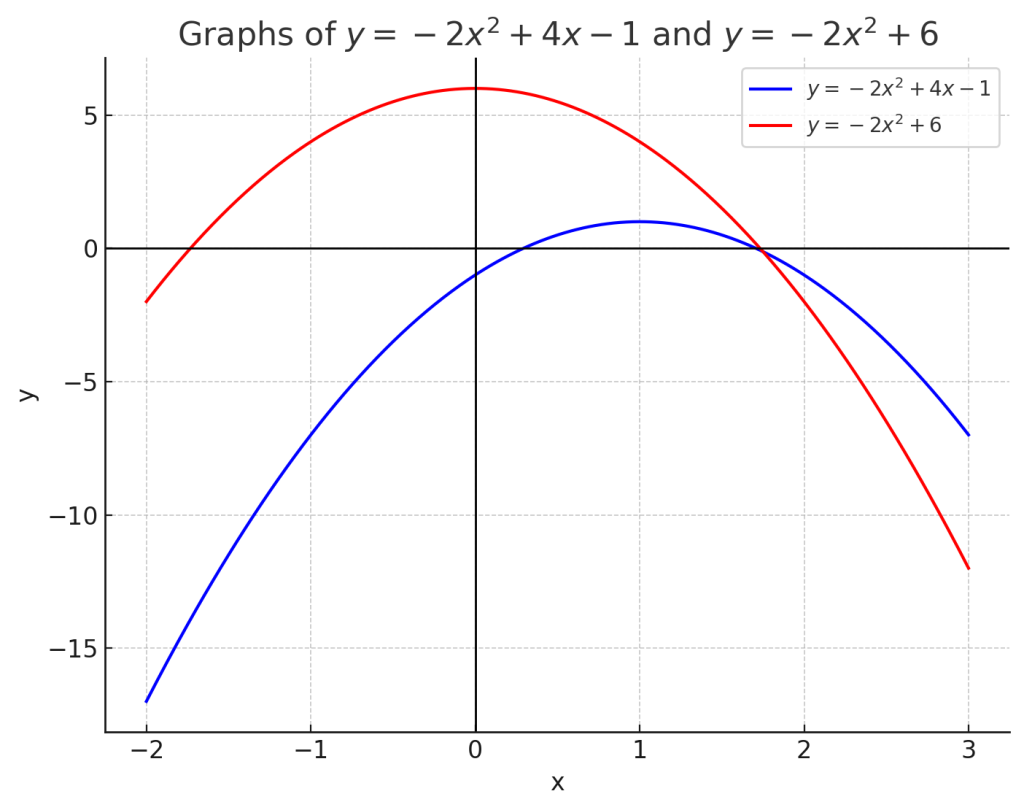
したがって、平行移動後の二次関数は
\[ \begin{align*} y &= -2(x + 1)^2 + 4(x + 1) + 4 \\ &= -2(x^2 + 2x + 1) + 4(x + 1) + 4 \\ &= -2x^2 – 4x – 2 + 4x + 4 + 4 \\ &= -2x^2 + (-4x + 4x) + (-2 + 4 + 4) \\ &= -2x^2 + 6 \end{align*} \]
となります。
4.3. 例題 3:二次関数の頂点
平行移動前の頂点の座標を求める。平方完成をすると
\[ \begin{align*} y &= 3x^2 – 6x + 2 \\ &= 3(x^2 – 2x) + 2 \\ &= 3\left( (x – 1)^2 – 1 \right) + 2 \\ &= 3(x – 1)^2 – 3 + 2 \\ &= 3(x – 1)^2 – 1 \end{align*} \]
二次関数の頂点の座標は \( (1, -1) \) です。
\( x \)-軸方向に 2 だけ平行移動 → \( x = 1 + 2 = 3 \)
\( y \)-軸方向に 3 だけ平行移動 → \( y = -1 + 3 = 2 \)
したがって、平行移動後の頂点の座標は \( (3, 2) \) となります。