二次形式と標準形、最大値最小値について

1. 二次形式の定義
線形代数において、二次形式は特定の形を持つ関数で、主にベクトルと行列を使って表されます。二次形式の一般的な定義は次のようになります。
\[ Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x} \]
ここで、$\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}$となるベクトル。\( \mathbf{x}^T \) は \( \mathbf{x} \) の転置ベクトルを表します。行列 \( A \) は、対称行列である。\( A = A^T \)を満たしているとする。
1.1. 二次形式の具体例
例として、二次形式を具体的に見てみましょう。以下の行列 \( A \) とベクトル \( \mathbf{x} \) を考えます。
\[ A = \begin{bmatrix} 3 & 2 \\ 2 & 6 \end{bmatrix}, \quad \mathbf{x} = \begin{bmatrix} x \\ y \end{bmatrix} \]
二次形式 \( Q \) は次のように計算されます。
\[ \begin{align*} Q(\mathbf{x}) &= \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 3 & 2 \\ 2 & 6 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \\ &= \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} 3x + 2y \\ 2x + 6y \end{bmatrix} \\ &= x(3x + 2y) + y(2x + 6y) \\ &= 3x^2 + 4xy + 6y^2 \end{align*} \]
この式は \( x \) と \( y \) の二次の項と、それらの積である項を含んでいます。
1.2. 2変数の二次形式
2変数 \( x \) と \( y \) の場合、一般的な対称行列 \( A \) とベクトル \( \mathbf{x} = \begin{bmatrix} x \\ y \end{bmatrix} \) を使って次のように二次形式を定義します。
\[ A = \begin{bmatrix} a & b \\ b & c \end{bmatrix} \]
としたとき、二次形式$Q(\mathbf x)$は次のように計算できます。
$$\begin{align*} Q(\mathbf{x}) &= \mathbf{x}^T A \mathbf{x} = \begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} a & b \\ b & c \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \\ &= x(ax + by) + y(bx + cy) \\ &= ax^2 + 2bxy + cy^2 \end{align*}$$
1.3. 3変数の二次形式
3変数 \( x \), \( y \), \( z \) の場合、一般的な対称行列 \( A \) とベクトル \( \mathbf{x} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} \) を使って次のように二次形式を定義します。
\[ A = \begin{bmatrix} a & b & c \\ b & d & e \\ c & e & f \end{bmatrix} \]
としたとき、二次形式$Q(\mathbf x)$は次のように計算できます。
$$\begin{align*} Q(\mathbf{x}) &= \mathbf{x}^T A \mathbf{x} = \begin{bmatrix} x & y & z \end{bmatrix} \begin{bmatrix} a & b & c \\ b & d & e \\ c & e & f \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} \\ &= x(ax + by + cz) + y(bx + dy + ez) + z(cx + ey + fz) \\ &= ax^2 + dy^2 + fz^2 + 2bxy + 2cxz + 2eyz \end{align*}$$
2. 二次形式の標準形
\[ Q(x_1,x_2,\cdots x_n) = \lambda_1 x_1^2 + \lambda_2 x_2^2 + \ldots + \lambda_n x_n^2 \]ここで、\( \lambda_i \)はスカラー値です。
2.1. 標準形への変換
二次形式を標準形に変換するためには、適切な直交行列\( U \)を見つけ、座標変換を行います。
対称行列\( A \)を対角化するために、固有ベクトルからなる直交行列\( U \)を求めます。\( A \)が対称行列である場合、直行行列で対角化ができます。これを使って、\[ U^T A U = D \]ここで\( D \)は対角行列で、その対角成分には\( A \)の固有値が並びます。
$$D=\begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix}$$
\( x= U x’ \)と定義します。これにより二次形式は、
\[ x^{T}Ax = (U^T x’)^T A (U^T x’) = x’^T U^T A U x’ = x’^T U^{-1} A U x’ = x’^T D x’ \]
となります。ここで、Uは直行行列であることより、$U^T=U^{-1}$となることを用いました。
\( D \)の対角成分(固有値)が\( \lambda_i \)となるため、標準形は
\[ Q(x_1,x_2,\cdots x_n) = \lambda_1 x_1^2 + \lambda_2 x_2^2 + \ldots + \lambda_n x_n^2 \]
となります。
2.2. 二次形式の標準形の例題
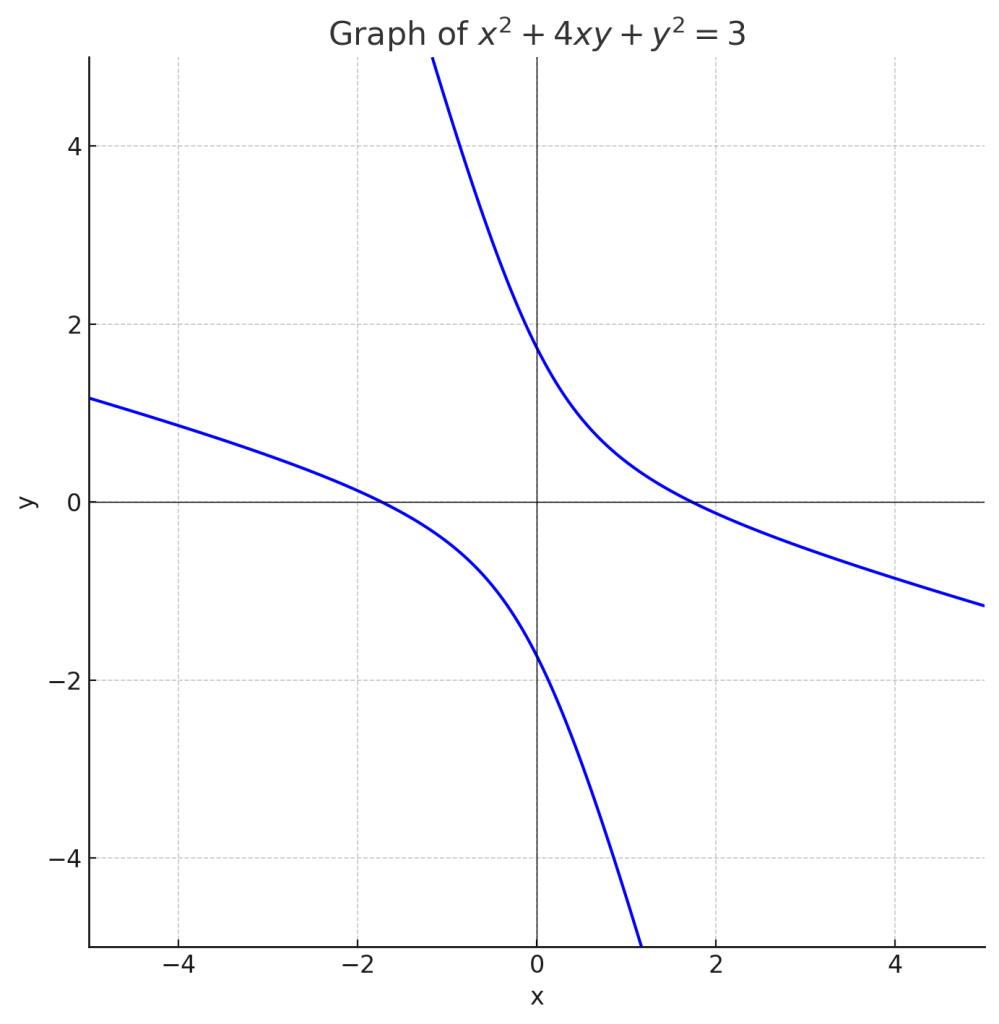
次の二次形式を標準化せよ。
$x^2+4xy+y^2=3$
ベクトル\( \mathbf{x} =\begin{bmatrix} x \\ y \end{bmatrix} \)とする。与えられた2次形式は次のように表すことができる。
$x^2+4xy+y^2$
$=\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix}1 & 2 \\ 2 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}$
$=x^T A x$
とあらわすことができる。
次にAを対角化するために、固有方程式を解く。
$\det(A-\lambda E)$
$= \begin{vmatrix} 1-\lambda & 2 \\ 2 & 1-\lambda \end{vmatrix}$
$= (1-\lambda)(1-\lambda) – 2 \times 2 = \lambda^2 – 2\lambda + 1 – 4 = \lambda^2 – 2\lambda – 3$
この方程式を因数分解すると、
\[ (\lambda – 3)(\lambda + 1) = 0 \]
したがって、固有値は \( \lambda = 3 \) と \( \lambda = -1 \) です。
次に、これらの固有値に対応する固有ベクトルを求めます。
[1]固有値 \( \lambda = -1 \) であるとき
\[
\begin{bmatrix} 2 & 2 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
\]
$rank \begin{bmatrix} 2 & 2 \\ 2 & 2 \end{bmatrix} = 1$より、解の自由度が1であるため、任意定数kを用いて、$x=k$とすると、
固有ベクトルは、$$\begin{bmatrix} x \\ y \end{bmatrix} =k\begin{bmatrix} 1 \\ -1 \end{bmatrix}$$となる。$u_1=\dfrac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ -1 \end{bmatrix}$とする。
[2]固有値 \( \lambda = 3 \) であるとき、
\[ \begin{bmatrix} -2 & 2 \\ 2 & -2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \]
$rank \begin{bmatrix} -2 & 2 \\ 2 & -2 \end{bmatrix} = 1$より、解の自由度が1であるため、任意定数kを用いて、$x=k$とすると、
固有ベクトルは、$$\begin{bmatrix} x \\ y \end{bmatrix} =k\begin{bmatrix} 1 \\ 1 \end{bmatrix}$$となる。$u_2==\dfrac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 1 \end{bmatrix}$とする。
次に、直行行列$U=\begin{bmatrix} u_1 & u_2\end{bmatrix}==\dfrac{1}{\sqrt{2}}\begin{bmatrix}1 & 1 \\ -1 & 1 \end{bmatrix}$とする。
$x = Ux’$と置き、$x^T A x$の式に代入すると、
$x^T A x$
$=(Ux’)^T A Ux’$
$=x’^T U^T A Ux’$
$=x’^T U^{-1} A Ux’$
$=x’^T \begin{bmatrix} -1 & 0 \\0 & 3 \end{bmatrix}x’$
$=-x^2+3y^2$
になる。したがって、
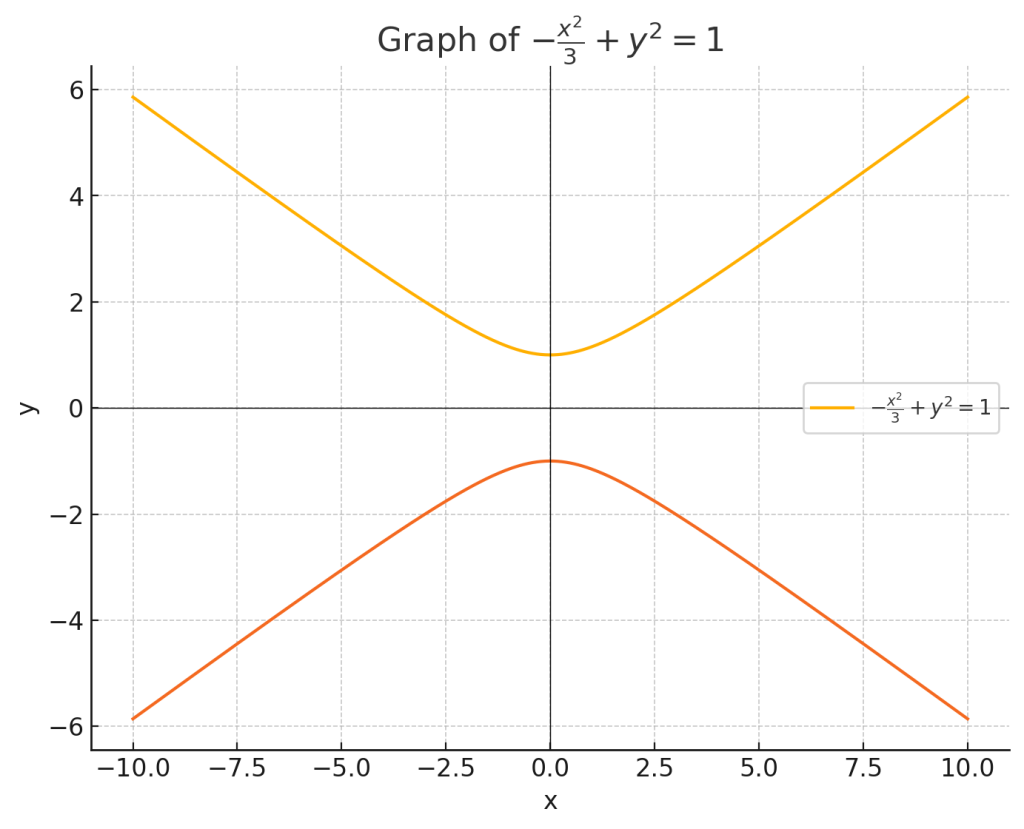
$-\dfrac{x^2}{3}+y^2 = 1$
となる。
2.2.1. それぞれのグラフ
3. 二次形式の最大値・最小値
制約条件$\displaystyle\sum ^n _{i=1} x_i^2 =1$であるとき、二次形式の最大値は固有値の最大値、最小値は固有値の最小値になる。
$\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}$ $\mathbf{x’}=\begin{bmatrix} x_1′ \\ x_2′ \\ \vdots \\ x_n’ \end{bmatrix}$とします。直行行列を用いて、$\mathbf{x} =U\mathbf{x’}$と直行変換を行うとします。制約条件より、
$\displaystyle\sum ^n _{i=1} x_i^2 $
$=\mathbf{x^T}\mathbf{x}$
$=(U^T\mathbf{x’})^T U\mathbf{x’}$
$=\mathbf{x’}U^{-1}U\mathbf{x’}$
$=\mathbf{x’}^T\mathbf{x’}$
$=\displaystyle\sum^n_{i=1} (x’_i)^2$
$=1$
したがって、$\displaystyle\sum^n_{i=1} (x’_i)^2=1$であることがわかりました。
任意の二次形式$Q(x_1,x_2,\cdots x_n)$を標準形に変換すると、
\[ Q(x_1,x_2,\cdots x_n) = (\lambda_1 x^{‘}_1)^2 + (\lambda_2 x^{‘}_2)^2 + \ldots + (\lambda_n x^{‘}_n)^2 \]
$\lambda_i$は固有値とする。
ここで、$\lambda_{\max}$を最大の固有値、$\lambda_{\min}$を最小の固有値とします。したがって、次の不等式が成立します。
\[ \lambda_{\min} \displaystyle\sum_{i=1}^n (x’_i)^2 \leq Q \leq \lambda_{\max} \displaystyle\sum_{i=1}^n (x’_i)^2 \]
これにより、
\[ \lambda_{\min} \leq Q \leq \lambda_{\max} \]となります。