数直線で考える二次不等式の解法について

1. 二次不等式
二次不等式とは、二次の項を含む次のような不等式のことを言います。
\[ ax^2 + bx + c > 0 \]
\[ ax^2 + bx + c \geq 0 \]
\[ ax^2 + bx + c < 0 \]
\[ ax^2 + bx + c \leq 0 \]
ここで \(a\)、\(b\)、\(c\) は定数です。また、$a\neq 0$です。
2. 不等式の解き方
2.1. 0以上または0より大きい場合
$a > 0$とし、$p < q$とします。このとき、$a(x – p)(x – q) > 0$の不等式が成り立つ条件を考えます。まず、$a > 0$なので、方程式の符号は$x – p$と$x – q$の符号に依存します。この不等式が成り立つためには、次の2つのケースが考えられます。
[1]$x – p > 0$ かつ $x – q > 0$ の場合
[2]$x – p < 0$ かつ $x – q < 0$ の場合
[1]$x – p > 0$ かつ $x – q > 0$ の場合
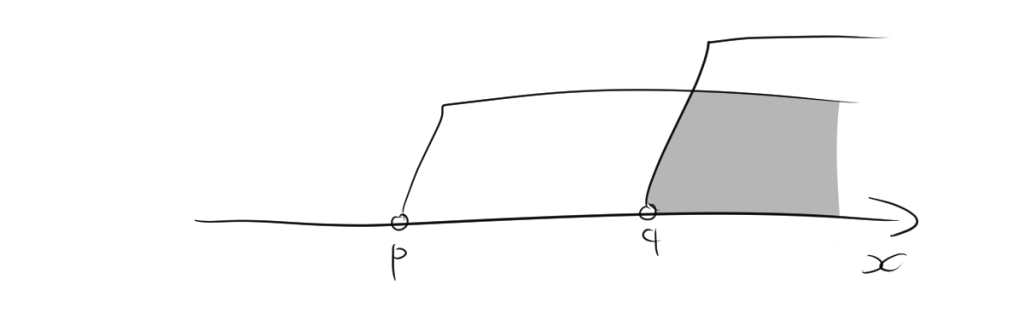
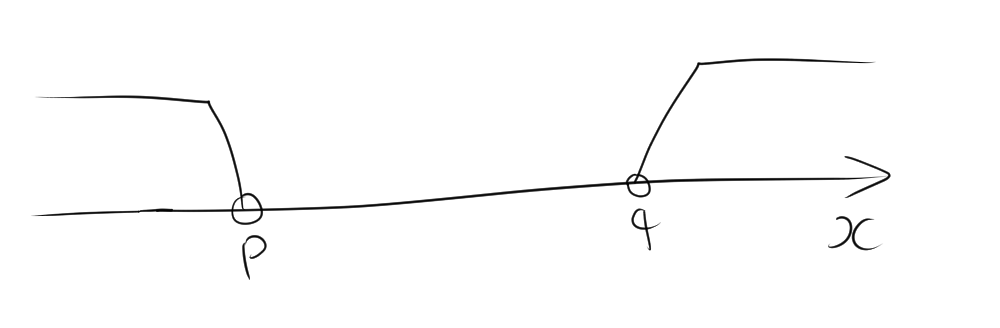
$x – p > 0$かつ$x – q > 0$は、それぞれ$x > p$および$x > q$を意味します。これを数直線上で考えると、$x$が$p$と$q$の両方よりも大きい領域にあることがわかります。数直線上で表すと、この領域は以下のようになります。
つまり、$x > q$の範囲がこの場合の解になります。
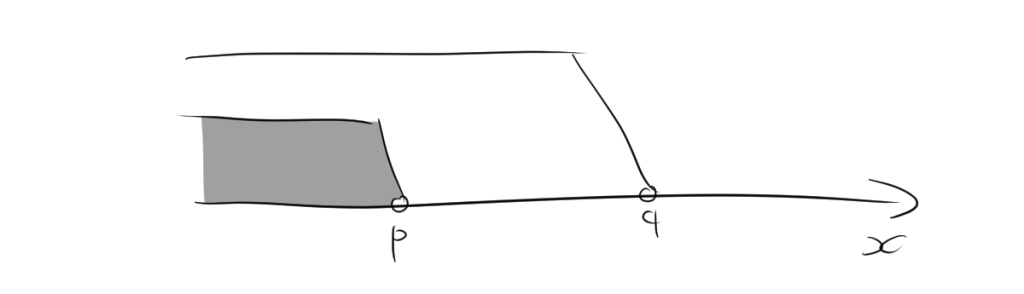
[2]$x – p < 0$ かつ $x – q < 0$ の場合
次に、$x – p < 0$かつ$x – q < 0$のケースを考えます。数直線上で考えると、$x < p$の範囲で不等式が成立します。
以上より、$a(x – p)(x – q) > 0$が成立するのは、次の2つの条件のいずれかが成り立つときです。
$$x > q \quad \text{または} \quad x < p$$
$a(x – p)(x – q) \geqq 0$の場合も同様に考えて
$$x \geqq q \quad \text{または} \quad x \leqq p$$
2.2. 0以下または0より小さい場合
$a > 0$とし、$p < q$とします。このとき、$a(x – p)(x – q) < 0$が成り立つ条件を考えます。$a > 0$なので、方程式の符号は$x – p$と$x – q$の符号に依存します。この不等式が成り立つためには、次のようなケースが考えられます。
[1]$x – p > 0$ かつ $x – q < 0$ の場合
[2]$x – p < 0$ かつ $x – q > 0$ の場合
[1] $x – p > 0$ かつ $x – q < 0$ の場合
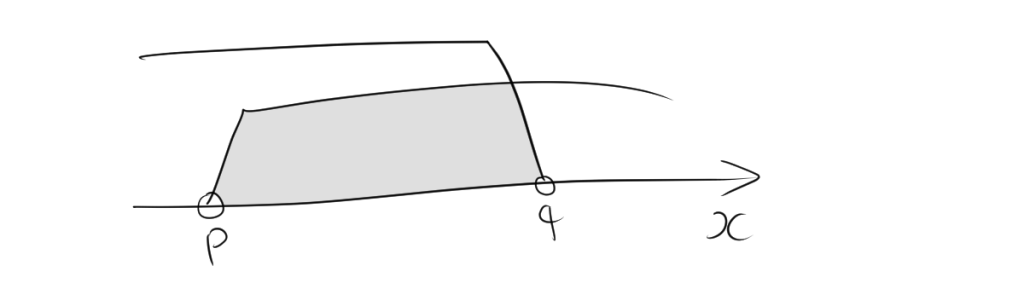
この条件は、$x > p$ かつ $x < q$となるので、$x$は$p$より大きく$q$より小さい範囲、すなわち$p < x < q$の範囲にあります。数直線上では、この領域は次のように表されます。
[2]$x – p < 0$ かつ $x – q > 0$ の場合
この条件は、$x > q$ かつ $x < p$を意味します。しかし、この条件を満たす$x$は存在しません。なぜなら、$p < q$という前提があるため、$x$が同時に$q$より大きく、$p$より小さい範囲は存在しないからです。また、数直線上では、この領域は次のように表されます。
以上より、$a(x – p)(x – q) < 0$が成立するのは、次の条件が成り立つときです。
$$p < x < q$$
$a(x – p)(x – q) \leqq 0$が成立するのは、次の条件が成り立つときです。
$$p \leqq x \leqq q$$
3. 二次不等式の例題
3.1. 例題1
\[ x^2 – 3x – 4 < 0 \]
まず、因数分解します。
\[ (x – 4)(x + 1) < 0 \]
したがって、xの範囲は$-1<x<4$となる。
3.2. 例題2
\[ x^2 – 4x – 2 \geqq 0 \]
二次方程式の解の公式より、
$$x=2\pm\sqrt{2^2+2}=2\pm \sqrt{6}$$
因数分解します。
\[ (x – (2-\sqrt{6}))(x – (2+\sqrt{6}) \geqq 0 \]
したがって、xの範囲は$2-\sqrt{6} \leqq x \leqq 2+\sqrt{6}$となる。
3.3. 例題3
\[ x^2 – 2x +2 \geqq 0 \]
平方完成をすると、
$$x^2 – 2x +2 =(x-1)^2+1 >0$$
となるので、常に正である。したがって、xの範囲は実数全体である。
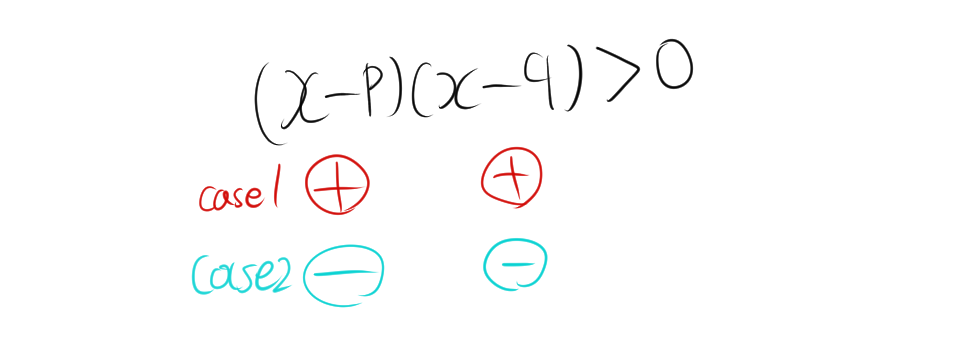
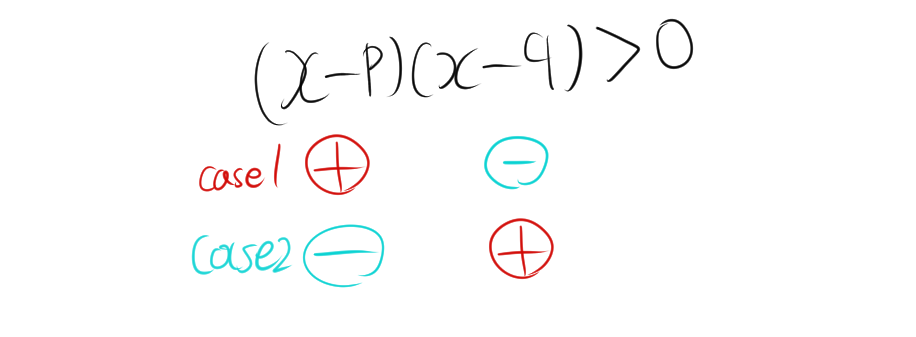



の不等式.png.webp)