グラフで考える二次不等式の解き方について

1. 二次不等式
二次不等式とは、二次の項を含む次のような不等式のことを言います。
\[ ax^2 + bx + c > 0 \]
\[ ax^2 + bx + c \geq 0 \]
\[ ax^2 + bx + c < 0 \]
\[ ax^2 + bx + c \leq 0 \]
ここで \(a\)、\(b\)、\(c\) は定数です。また、$a\neq 0$です。
1.1. グラフを利用した解法
- 因数分解をする。因数分解が厳しい場合、二次方程式の解の公式または平方完成をする。
- y=0(x軸)の位置関係を考える
1.2. 具体例
次の二次不等式を解いてみましょう。
\[ -2x^2 + 4x – 1 > 0 \]
平方完成すると、
\[ \begin{align*} -2x^2 + 4x – 1 &= 0 \\ -2(x-1)^2 + 1 &= 0 \end{align*} \]
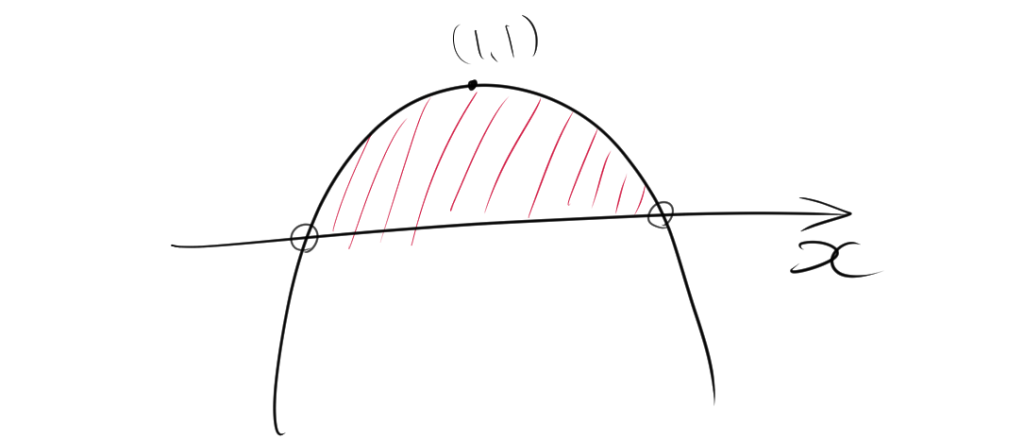
したがって、位置関係は次のようになります。
方程式 \( -2x^2 + 4x – 1 = 0 \) を解くと、
\[ \begin{align*} -2(x-1)^2 &= -1 \\ (x-1) &= \pm\frac{1}{\sqrt{2}} \\ x &= 1 \pm \frac{1}{\sqrt{2}} \end{align*} \]
したがって、図の赤色の範囲が求めるxの範囲であるので、
$$1 – \frac{1}{\sqrt{2}}<x< 1 + \frac{1}{\sqrt{2}}$$
1.3. グラフの重要性
二次不等式を理解する上で、グラフの視覚的なイメージは非常に重要です。グラフを見ることで、関数がx軸のどこで交わるかや、どの範囲で不等式が成り立つかが直感的に理解できるようになります。特に、複雑な不等式の場合には、グラフが解決の手助けをしてくれます。
2. 二次不等式の例題
2.1. 例題1
$$x^2+x+1<0$$
不等式 \( x^2 + x + 1 < 0 \) を平方完成を使って解いていきましょう。
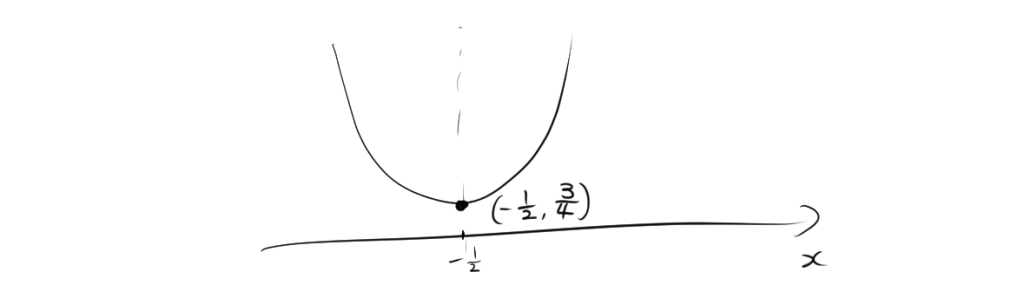
\[ x^2 + x + 1 = \left( x + \frac{1}{2} \right)^2 – \frac{1}{4} + 1 = \left( x + \frac{1}{2} \right)^2 + \frac{3}{4} \]
したがって、グラフを書くと、
不等式 \( x^2 + x + 1 \) は常に正であるので、満たす解は存在しません。
2.2. 例題2
$$x^2+2x+1>0$$
不等式 \(x^2 + 2x + 1 > 0\) を解いていきます。
まず、左辺の式 \(x^2 + 2x + 1\) を因数分解します。
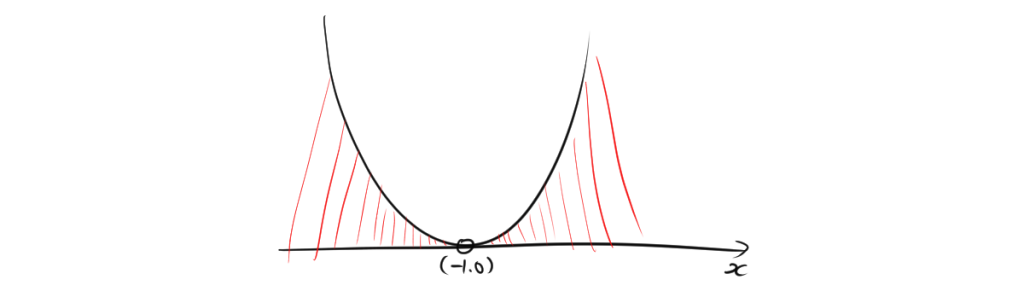
\[ x^2 + 2x + 1 = (x + 1)^2 \]
したがって、不等式は次のように書き換えられます。
\[ (x + 1)^2 > 0 \]
グラフを書くと、
この不等式 \( (x + 1)^2 > 0 \) は、\( x \neq -1 \) のときに成り立ちます。つまり、xの範囲は-1を除く実数である。